题目内容
2. 质谱仪的工作原理如图示,一个质量为m,电荷量为 q的带正电粒子,经过电压为U的加速电场由静止加速后,刚好直线进入速度选择器.速度选择器内有相互垂直的匀强磁场和匀强电场E.直线通过选择器的粒子经狭缝P后进入到偏转磁场,最后打在胶片A1A2上,且离P点的距离为L.求:
质谱仪的工作原理如图示,一个质量为m,电荷量为 q的带正电粒子,经过电压为U的加速电场由静止加速后,刚好直线进入速度选择器.速度选择器内有相互垂直的匀强磁场和匀强电场E.直线通过选择器的粒子经狭缝P后进入到偏转磁场,最后打在胶片A1A2上,且离P点的距离为L.求:(1)粒子离开加速电场时速率是多少?
(2)速度选择器中磁场B的大小和方向?
(3)偏转磁场B0大小?
分析 (1)粒子在电场中运动只有电场力做功,根据动能定理可以求得粒子从加速电场射出时速度v的大小;
(2)带电的粒子在速度选择器中做匀速直线运动,说明粒子受力平衡,根据粒子的受力状态可以求得速度选择器中匀强磁场的磁感应强度B的大小,根据左手定则判断B的方向;
(3)粒子在磁场中做匀速圆周运动,根据粒子在磁场中运动的半径公式可以求得偏转磁场的磁感应强度B0的大小.
解答 解:(1)在加速电场,据动能定理,有:
qU=$\frac{1}{2}m{V^2}$
粒子离开时速率为:$V=\sqrt{\frac{2qU}{m}}$
(2)据左手定则,知速度选择器中磁场方向为垂直纸面向外,根据二力平衡,有:
q V B=q E
解得:B=$\frac{E}{V}$=E $\sqrt{\frac{m}{2qU}}$
(3)粒子在偏转磁场做圆周运动,洛伦兹力提供向心力,即:
q V B0=$m\frac{V^2}{R}$
由题意得:R=$\frac{L}{2}$
故偏转磁场B0 大小为:B0=$\frac{2}{L}\sqrt{\frac{2mU}{q}}$
答:(1)粒子离开加速电场时速率是$\sqrt{\frac{2qU}{m}}$
(2)速度选择器中磁场B的大小$E\sqrt{\frac{m}{2qU}}$和方向垂直纸面向外
(3)偏转磁场B0大小$\frac{2}{L}\sqrt{\frac{2mU}{m}}$
点评 粒子在速度选择器中的运动可以分为匀加速直线运动、匀速运动和匀速圆周运动,根据不同阶段的运动的特点来分类解决.

练习册系列答案
相关题目
11. 如图所示,一容器中装满水,水中有一轻弹簧下端与容器相连,上端与一木球相连,关于此装置在下列运动说法正确的是( )
如图所示,一容器中装满水,水中有一轻弹簧下端与容器相连,上端与一木球相连,关于此装置在下列运动说法正确的是( )
 如图所示,一容器中装满水,水中有一轻弹簧下端与容器相连,上端与一木球相连,关于此装置在下列运动说法正确的是( )
如图所示,一容器中装满水,水中有一轻弹簧下端与容器相连,上端与一木球相连,关于此装置在下列运动说法正确的是( )| A. | 静止时弹簧处于原长 | |
| B. | 整个装置自由下落时,由于浮力的作用,弹簧处于拉伸状态 | |
| C. | 整个装置自由下落时,弹簧处于原长 | |
| D. | 整个装置自由下落时,小球的重力消失 |
 “测定玻璃的折射率”实验中,在玻璃砖的一侧竖直插两个大头针A、B,在另一侧再竖直插两个大头针C、D.在插入第四个大头针D时,要使它挡住C和A、B的像.
“测定玻璃的折射率”实验中,在玻璃砖的一侧竖直插两个大头针A、B,在另一侧再竖直插两个大头针C、D.在插入第四个大头针D时,要使它挡住C和A、B的像. 如图所示,经过专业训练的杂技运动员进行爬杆表演,运动员先爬上8m高的固定竖直金属杆,然后双腿夹紧金属杆倒立,头顶离地面7m高,运动员通过双腿对金属杆施加不同的压力来控制身体的运动情况.首先,运动员匀加速下滑3m,速度达到 4m/s,然后匀减速下滑,当运动员头项刚要接触地面时,速度刚好减到零,设运动员质量为50kg.
如图所示,经过专业训练的杂技运动员进行爬杆表演,运动员先爬上8m高的固定竖直金属杆,然后双腿夹紧金属杆倒立,头顶离地面7m高,运动员通过双腿对金属杆施加不同的压力来控制身体的运动情况.首先,运动员匀加速下滑3m,速度达到 4m/s,然后匀减速下滑,当运动员头项刚要接触地面时,速度刚好减到零,设运动员质量为50kg. 某研究性学习小组利用插针法可以测量半圆形玻璃砖的折射率.实验探究方案如下:在白纸上做一直线MN,并做出它的一条垂线AB,将半圆柱形玻璃砖(底面的圆心为O)放在白纸上,它的直边与直线MN对齐,在垂线AB上插两个大头针P1和P2,然后在半圆柱形玻璃砖的右侧插上适量的大头针,可以确定光线P1P2通过玻璃砖后的光路,从而求出玻璃的折射率.实验中提供的器材除了半圆柱形玻璃砖、木板和大头针外,还有量角器等.
某研究性学习小组利用插针法可以测量半圆形玻璃砖的折射率.实验探究方案如下:在白纸上做一直线MN,并做出它的一条垂线AB,将半圆柱形玻璃砖(底面的圆心为O)放在白纸上,它的直边与直线MN对齐,在垂线AB上插两个大头针P1和P2,然后在半圆柱形玻璃砖的右侧插上适量的大头针,可以确定光线P1P2通过玻璃砖后的光路,从而求出玻璃的折射率.实验中提供的器材除了半圆柱形玻璃砖、木板和大头针外,还有量角器等. 用如图所示的浅色水平传送带AB和斜面BC将货物运送到斜面的顶端.AB距离L=11m,传送带始终以v=12m/s匀速顺时针运行.传送带B端靠近倾角θ=37°的斜面底端,斜面底端与传送带的B端之间有一段长度可以不计的小圆弧.在A、C处各有一个机器人,A处机器人每隔t=1.0s将一个质量m=10kg、底部有碳粉的货物箱(可视为质点)轻放在传送带A端,货物箱经传送带和斜面后到达斜面顶端的C点时速度恰好为零,C点处机器人立刻将货物箱搬走.已知斜面BC的长度s=5.0m,传送带与货物箱之间的动摩擦因数μ0=0.55,货物箱由传送带的右端到斜面底端的过程中速度大小损失原来的$\frac{1}{11}$,不计传送带轮的大小,g=10m/s2(sin37°=0.6,cos37°=0.8).求:
用如图所示的浅色水平传送带AB和斜面BC将货物运送到斜面的顶端.AB距离L=11m,传送带始终以v=12m/s匀速顺时针运行.传送带B端靠近倾角θ=37°的斜面底端,斜面底端与传送带的B端之间有一段长度可以不计的小圆弧.在A、C处各有一个机器人,A处机器人每隔t=1.0s将一个质量m=10kg、底部有碳粉的货物箱(可视为质点)轻放在传送带A端,货物箱经传送带和斜面后到达斜面顶端的C点时速度恰好为零,C点处机器人立刻将货物箱搬走.已知斜面BC的长度s=5.0m,传送带与货物箱之间的动摩擦因数μ0=0.55,货物箱由传送带的右端到斜面底端的过程中速度大小损失原来的$\frac{1}{11}$,不计传送带轮的大小,g=10m/s2(sin37°=0.6,cos37°=0.8).求: 如图所示,m=1kg的物体静止在水平粗糙地面上,μ=0.5,对物块施加一个与水平方向夹角为37°斜向上F=10N的力,物体做匀加速直线运动,经过t=1s后撤掉F,物体最终静止,求整个过程中物体发生的位移大小(g=10m/s2、sin37°=0.6、cos37°=0.8)
如图所示,m=1kg的物体静止在水平粗糙地面上,μ=0.5,对物块施加一个与水平方向夹角为37°斜向上F=10N的力,物体做匀加速直线运动,经过t=1s后撤掉F,物体最终静止,求整个过程中物体发生的位移大小(g=10m/s2、sin37°=0.6、cos37°=0.8)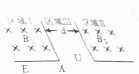 如图所示是某中学学生根据回旋加速器原理设计的一个小型粒子加速器的原理示意图,区域Ⅰ和区域Ⅱ存在匀强磁场B1和B2.在宽度为d的区域Ⅲ内存在一个匀强电场,电势差大小为U,通过自动调整两区域间的电势高低可使进入该区域的电势差大小恒为U,通过自动调整两区域间的电势高低可使进入该区域的粒子持续加速.在图中A位置静止释放一个质量为m,带电量为q的正电粒子(重力不计),粒子经过两次电场加速后最终垂直于区域Ⅰ边缘AE射出,一切阻力不计,求:
如图所示是某中学学生根据回旋加速器原理设计的一个小型粒子加速器的原理示意图,区域Ⅰ和区域Ⅱ存在匀强磁场B1和B2.在宽度为d的区域Ⅲ内存在一个匀强电场,电势差大小为U,通过自动调整两区域间的电势高低可使进入该区域的电势差大小恒为U,通过自动调整两区域间的电势高低可使进入该区域的粒子持续加速.在图中A位置静止释放一个质量为m,带电量为q的正电粒子(重力不计),粒子经过两次电场加速后最终垂直于区域Ⅰ边缘AE射出,一切阻力不计,求: