题目内容
15.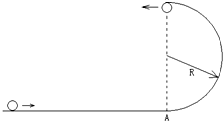 如图所示,小球沿光滑的水平面冲上一个光滑的半圆形轨道,已知轨道的半径为R,小球到达轨道的最高点时对轨道的压力大小恰好等于小球的重力.请求出:
如图所示,小球沿光滑的水平面冲上一个光滑的半圆形轨道,已知轨道的半径为R,小球到达轨道的最高点时对轨道的压力大小恰好等于小球的重力.请求出:(1)小球到达轨道最高点时的速度为多大?
(2)小球落地时距离A点多远?
(3)落地时速度多大?
分析 (1)根据牛顿第二定律,结合最高点的压力大小,求出小球到达轨道最高点时的速度大小.
(2)根据高度求出平抛运动的时间,结合最高点的速度和时间求出小球落地时距离A点多远.
(3)根据速度时间公式求出落地时竖直分速度,结合平行四边形定则求出落地的速度.
解答 解:(1)在最高点,根据牛顿第二定律得,mg+${F}_{N}=m\frac{{{v}_{1}}^{2}}{R}$,
因为mg=FN1,解得${v}_{1}=\sqrt{2gR}$.
(2)根据2R=$\frac{1}{2}g{t}^{2}$得,平抛运动的时间t=$\sqrt{\frac{4R}{g}}$,
则小球落地时距离A点距离x=${v}_{1}t=\sqrt{2gR}×\sqrt{\frac{4R}{g}}=2\sqrt{2}R$.
(3)小球落地时竖直分速度${v}_{y}=gt=g×\sqrt{\frac{4R}{g}}=\sqrt{4gR}$,
根据平行四边形定则知,落地的速度v=$\sqrt{{{v}_{1}}^{2}+{{v}_{y}}^{2}}$=$\sqrt{2gR+4gR}$=$\sqrt{6gR}$.
答:(1)小球到达轨道最高点时的速度为$\sqrt{2gR}$;
(2)小球落地时距离A点$2\sqrt{2}R$;
(3)落地时速度为$\sqrt{6gR}$.
点评 本题考查了平抛运动、圆周运动与牛顿定律和运动学公式的综合运用,知道平抛运动在水平方向和竖直方向上的运动规律,以及圆周运动向心力的来源是解决本题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
5. 发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使 其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道 1、2相切于Q点,轨道2、3相切于P 点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )
发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使 其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道 1、2相切于Q点,轨道2、3相切于P 点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )
 发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使 其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道 1、2相切于Q点,轨道2、3相切于P 点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )
发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使 其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道 1、2相切于Q点,轨道2、3相切于P 点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )| A. | 卫星在轨道2上经过P点时的速度等于它在轨道3上经过P点时的速度 | |
| B. | 卫星在轨道2上经过P点时的速度小于它在轨道3上经过P点时的速度 | |
| C. | 卫星在轨道1上经过Q点时的加速度大于它在轨道2上经过Q点时的加速度 | |
| D. | 卫星在轨道2上经过P点时的加速度等于它在轨道3上经过P点时的加速度 |
3.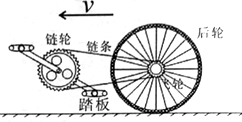 小明同学在学习了圆周运动的知识后,设计了一个通过测量脚板的转数,推算自行车的骑行速度的方法.他的设想是:测量后轮的半径R,飞轮的齿数N1,链轮的齿数N2,当测得链轮(即脚踏板)的转速为n($\frac{r}{s}$)时,可推算自行车前进速度v的表达式为( )
小明同学在学习了圆周运动的知识后,设计了一个通过测量脚板的转数,推算自行车的骑行速度的方法.他的设想是:测量后轮的半径R,飞轮的齿数N1,链轮的齿数N2,当测得链轮(即脚踏板)的转速为n($\frac{r}{s}$)时,可推算自行车前进速度v的表达式为( )
 小明同学在学习了圆周运动的知识后,设计了一个通过测量脚板的转数,推算自行车的骑行速度的方法.他的设想是:测量后轮的半径R,飞轮的齿数N1,链轮的齿数N2,当测得链轮(即脚踏板)的转速为n($\frac{r}{s}$)时,可推算自行车前进速度v的表达式为( )
小明同学在学习了圆周运动的知识后,设计了一个通过测量脚板的转数,推算自行车的骑行速度的方法.他的设想是:测量后轮的半径R,飞轮的齿数N1,链轮的齿数N2,当测得链轮(即脚踏板)的转速为n($\frac{r}{s}$)时,可推算自行车前进速度v的表达式为( )| A. | 2πn$\frac{{N}_{1}R}{{N}_{2}}$ | B. | 2πn$\frac{{N}_{2}R}{{N}_{1}}$ | C. | πn$\frac{{N}_{1}R}{{N}_{2}}$ | D. | πn$\frac{{N}_{2}}{{N}_{1}}$R |
7.某一物体在质量不变的情况下,下列说法中正确的是( )
| A. | 物体动量改变,其速度大小一定改变 | |
| B. | 物体的速度方向改变,其动量不一定改变 | |
| C. | 物体做平抛运动时,在任意相等的时间内动量的变化量相同 | |
| D. | 物体的动能不变,其动量可能改变 |
4.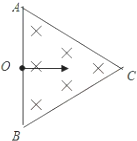 如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )
如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )
 如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )
如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )| A. | Bmin=$\frac{2m{v}_{0}}{qa}$,t=$\frac{7πa}{6v}$ | B. | Bmin=$\frac{2m{v}_{0}}{qa}$,t=$\frac{πa}{26v}$ | ||
| C. | Bmin=$\frac{6m{v}_{0}}{qa}$,t=$\frac{7πa}{6v}$ | D. | Bmin=$\frac{6m{v}_{0}}{qa}$,t=$\frac{πa}{26v}$ |
6. 如图所示,虚线表示某电场中的四个等势面,相邻等势面间的电势差相等,一不计重力的带负电的粒子从右侧垂直等势面φ4向左进入电场,运动轨迹与等势面分别交于a,b,c三点,则可以判断( )
如图所示,虚线表示某电场中的四个等势面,相邻等势面间的电势差相等,一不计重力的带负电的粒子从右侧垂直等势面φ4向左进入电场,运动轨迹与等势面分别交于a,b,c三点,则可以判断( )
 如图所示,虚线表示某电场中的四个等势面,相邻等势面间的电势差相等,一不计重力的带负电的粒子从右侧垂直等势面φ4向左进入电场,运动轨迹与等势面分别交于a,b,c三点,则可以判断( )
如图所示,虚线表示某电场中的四个等势面,相邻等势面间的电势差相等,一不计重力的带负电的粒子从右侧垂直等势面φ4向左进入电场,运动轨迹与等势面分别交于a,b,c三点,则可以判断( )| A. | φ1<φ2<φ3<φ4 | |
| B. | 粒子的运动轨迹和φ3等势面也可能垂直 | |
| C. | φ4等势面上各点场强处处相等 | |
| D. | 该区域可能是点电荷和无限大金属平板形成的电场 |
 做杂技表演的汽车从高台水平飞出,在空中运动一段时间后着地(忽略空气阻力).一架相机通过多次曝光,拍摄得到汽车在着地前后一段时间内的运动照片,如图所示(虚线为正方形格子).已知汽车长度为3.6m,相邻两次曝光的时间间隔相等,第三个像是刚好着地的时刻,由照片可以计算出汽车离开高台时的瞬时速度大小为12m/s,高台离地面的高度为11.25 m (取g=10m/s2).
做杂技表演的汽车从高台水平飞出,在空中运动一段时间后着地(忽略空气阻力).一架相机通过多次曝光,拍摄得到汽车在着地前后一段时间内的运动照片,如图所示(虚线为正方形格子).已知汽车长度为3.6m,相邻两次曝光的时间间隔相等,第三个像是刚好着地的时刻,由照片可以计算出汽车离开高台时的瞬时速度大小为12m/s,高台离地面的高度为11.25 m (取g=10m/s2).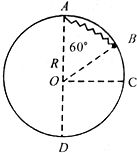 一个质量m=0.2kg的小球系于轻质弹簧的一端,且套在光滑竖直的圆环上的B点,弹簧的上端固定于环的最高点A,环的半径R=0.5m,弹簧的原长L0=0.5m,劲度系数为k=4.8N/m.如图所示,若小球从图中所示位置B点由静止开始滑动最低点D的过程中小球经过C点时的速度为vc=2m/s,小球到D点的速度vD=3m/s,重力加速度g=10m/s2,$\sqrt{2}$=1.414.求:
一个质量m=0.2kg的小球系于轻质弹簧的一端,且套在光滑竖直的圆环上的B点,弹簧的上端固定于环的最高点A,环的半径R=0.5m,弹簧的原长L0=0.5m,劲度系数为k=4.8N/m.如图所示,若小球从图中所示位置B点由静止开始滑动最低点D的过程中小球经过C点时的速度为vc=2m/s,小球到D点的速度vD=3m/s,重力加速度g=10m/s2,$\sqrt{2}$=1.414.求: