题目内容
9. 神奇的黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成,两星视为质点,不考虑其它天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示.引力常量为G,由观测能够得到可见星A的速率v和运行周期T.
神奇的黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成,两星视为质点,不考虑其它天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示.引力常量为G,由观测能够得到可见星A的速率v和运行周期T.(1)可见得A所受暗星B的引力FA可等效为位于O点处质量为m的星体(视为质点)对它的引力,设A和B的质量分别为m1、m2.试求m的值(用m1、m2表示);
(2)求暗星B的质量m2与可见星A的速率v、运行周期T和质量m1之间的关系式;
(3)恒星演化到末期,如果其质量大于太阳质量ms的两倍,它将有可能成为黑洞.若可见星A的速率v=2.7m/s,运行周期T=4.7π×104s,质量m1=6ms,试通过估算来判断暗星B有可能是黑洞吗?(G=6.67×10-11N•m/kg2,ms=2.0×1030kg)
分析 (1)抓住A、B做圆周运动的向心力相等,角速度相等,求出A、B轨道半径的关系,从而得知A、B距离为A卫星的轨道半径关系,可见星A所受暗星B的引力FA可等效为位于O点处质量为m的星体(视为质点)对它的引力,根据万有引力定律公式求出质量m.
(2)根据万有引力提供向心力求出暗星B的质量m2与可见星A的速率v、运行周期T和质量m1之间的关系式;
(3)根据第(2)问的表达式求出暗星B的质量,与太阳的质量进行比较,判断是否是黑洞.
解答 解:(1)设A、B的圆轨道半径分别为r1、r2,由题意知,A、B做匀速圆周运动的角速相同,其为ω.由牛顿运动定律,
有:FA=m1ω2r1,FB=m2ω2r2,FA=FB
设A、B之间的距离为r,又r=r1+r2,由上述各式得:r=$\frac{{m}_{1}+{m}_{2}}{{m}_{2}}{r}_{1}$…①
由万有引力定律,有:FA=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$,
将①代入得:FA=$G\frac{{m}_{1}{{m}_{2}}^{3}}{({m}_{1}+{m}_{2})^{2}{r}^{2}}$,令 FA=$G\frac{{m}_{1}m}{{{r}_{1}}^{2}}$,比较可得:m=$\frac{{{m}_{2}}^{3}}{{m}_{1}+{m}_{2}}$…②
(2)由牛顿第二定律,有:$G\frac{{m}_{1}m}{{{r}_{1}}^{2}}={m}_{1}\frac{{v}^{2}}{{r}_{1}}$…③
又可见星A的轨道半径为:r1=$\frac{vT}{2π}$…④
由②③④式可得,$\frac{{{m}_{2}}^{3}}{({m}_{1}+{m}_{2})^{2}}=\frac{{v}^{3}T}{2πG}$.
(3)将m1=6ms代入⑤式,得:$\frac{{{m}_{2}}^{3}}{(6{m}_{1}+{m}_{2})^{2}}=\frac{{v}^{3}T}{2πG}$,…⑤
代入数据得:$\frac{{{m}_{2}}^{3}}{(6{m}_{s}+{m}_{2})^{2}}$=3.5ms…⑥
设m2=nms,(n>0),将其代入⑥式,得:$\frac{{{m}_{2}}^{3}}{(6{m}_{s}+{m}_{2})^{2}}=\frac{n}{(\frac{6}{n}+1)^{2}}{m}_{s}=3.5{m}_{s}$…⑦
可见,$\frac{{{m}_{2}}^{3}}{(6{m}_{s}+{m}_{2})^{2}}$的值随n的增大而增大,试令n=2,得:
$\frac{n}{(\frac{6}{n}+1)^{2}}{m}_{s}$=0.125ms<3.5ms…⑧
若使⑦式成立,则n必须大于2,即暗星B的质量m2必须大于2ms,由此得出结论:暗星B有可能是黑洞.
答:(1)m的值为$\frac{{{m}_{2}}^{3}}{{m}_{1}+{m}_{2}}$;
(2)暗星B的质量m2与可见星A的速率v、运行周期T和质量m1之间的关系式为$\frac{{{m}_{2}}^{3}}{({m}_{1}+{m}_{2})^{2}}=\frac{{v}^{3}T}{2πG}$;
(3)暗星B有可能是黑洞.
点评 对于天体运动问题关键要建立物理模型.双星问题与人造地球卫星的运动模型不同,两星都绕着它们之间连线上的一点为圆心做匀速圆周运动,双星、圆心始终“三点”一线.

| A. | 保持质量不变,将它们间的距离增大到2R | |
| B. | 保持质量不变,将它们间的距离减小到原来的R/2 | |
| C. | 保持距离不变,将它们的质量都变为原来的2倍 | |
| D. | 将它们的质量及距离都变为原来的2倍 |
 经长期观测人们在宇宙中已经发现了“双星系统”,“双星系统”由两颗相距较近的恒星组成,每个恒星的线度远小于两个星体之间的距离,而且双星系统一般远离其他天体.如图所示,两颗星球组成的双星,在相互之间的万有引力作用下,绕连线上的O点做周期相同的匀速圆周运动.现测得两颗星之间的距离为L,质量之比为m1:m2=5:2.则可知( )
经长期观测人们在宇宙中已经发现了“双星系统”,“双星系统”由两颗相距较近的恒星组成,每个恒星的线度远小于两个星体之间的距离,而且双星系统一般远离其他天体.如图所示,两颗星球组成的双星,在相互之间的万有引力作用下,绕连线上的O点做周期相同的匀速圆周运动.现测得两颗星之间的距离为L,质量之比为m1:m2=5:2.则可知( )| A. | m1、m2做圆周运动的线速度之比为2:5 | |
| B. | m1、m2做圆周运动的角速度之比为5:2 | |
| C. | m1做圆周运动的半径为$\frac{2}{7}L$ | |
| D. | m2做圆周运动的半径为$\frac{2}{7}L$ |
 海南省文昌市建设了一个航天发射场,主要承担地球同步轨道卫星、大质量极轨卫星、大吨位空间站和深空探测卫星等航天器的发射任务.不可回收的航天器在使用后,将成为太空垃圾.如图所示是漂浮在地球附近的太空垃圾示意图,对此有如下说法,正确的是( )
海南省文昌市建设了一个航天发射场,主要承担地球同步轨道卫星、大质量极轨卫星、大吨位空间站和深空探测卫星等航天器的发射任务.不可回收的航天器在使用后,将成为太空垃圾.如图所示是漂浮在地球附近的太空垃圾示意图,对此有如下说法,正确的是( )| A. | 离地越高的太空垃圾运行周期越大 | |
| B. | 离地越高的太空垃圾运行的向心加速度越大 | |
| C. | 由公式V=$\sqrt{gR}$得,离地越高的太空垃圾运行速度越大 | |
| D. | 太空垃圾可能跟同一轨道上同向飞行的航天器相撞 |

| A. | 探测器的速度一直减小 | |
| B. | 探测器在距星球A为$\frac{L}{4}$处加速度为零 | |
| C. | 若探测器能到达星球B,其速度可能恰好为零 | |
| D. | 若探测器能到达星球B,其所受的合力先变小后变大 |
 如图所示为粮仓的传送带装置,一倾斜固定的传送带与水平方向成α=30°,且以恒定的大小为v0=2m/s的速度匀速向上传动,工人将一质量为m=50kg的粮袋由底端无初速地放到传送带上,经一段时间,粮袋运动到距离地面为h=2m的高处,粮袋与传送带间的动摩擦因数为μ=$\frac{\sqrt{3}}{2}$,g=10m/s2
如图所示为粮仓的传送带装置,一倾斜固定的传送带与水平方向成α=30°,且以恒定的大小为v0=2m/s的速度匀速向上传动,工人将一质量为m=50kg的粮袋由底端无初速地放到传送带上,经一段时间,粮袋运动到距离地面为h=2m的高处,粮袋与传送带间的动摩擦因数为μ=$\frac{\sqrt{3}}{2}$,g=10m/s2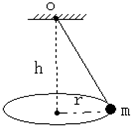 如图所示,在“用圆锥摆验证向心力表达式”的实验中,若测得小球质量为m,圆半径为r,小球到悬点大竖直高度为h,则小球所受向心力大小为$\frac{mgr}{h}$.
如图所示,在“用圆锥摆验证向心力表达式”的实验中,若测得小球质量为m,圆半径为r,小球到悬点大竖直高度为h,则小球所受向心力大小为$\frac{mgr}{h}$.