题目内容
9. 如图所示,一根轻质弹簧与质量为m的滑块P连接后,穿在一根光滑竖直杆上,弹簧下端与竖直杆的下端连接,一根轻绳跨过定滑轮将滑块P和重物Q连接起来.图中O、B两点等高,线段OA长为L,与水平方向的夹角θ=37°,重物Q的质量M=5m.把滑块从图中A点由静止释放后沿竖直杆上下运动,当它经过A、B两点时,弹簧对滑块的弹力大小相等,不计滑轮的摩擦.在滑块从A到B的运动过程中( )
如图所示,一根轻质弹簧与质量为m的滑块P连接后,穿在一根光滑竖直杆上,弹簧下端与竖直杆的下端连接,一根轻绳跨过定滑轮将滑块P和重物Q连接起来.图中O、B两点等高,线段OA长为L,与水平方向的夹角θ=37°,重物Q的质量M=5m.把滑块从图中A点由静止释放后沿竖直杆上下运动,当它经过A、B两点时,弹簧对滑块的弹力大小相等,不计滑轮的摩擦.在滑块从A到B的运动过程中( )| A. | 滑块P的速度一直增大 | B. | 滑块P在位置B的速度为vB=$\sqrt{\frac{4}{5}gL}$ | ||
| C. | 轻绳对滑块P做功mgL | D. | P与Q的机械能之和先增加后减小 |
分析 通过分析滑块P的受力情况,判断其运动情况,根据滑块通过A、B两点时弹簧的弹性势能相等,由系统的机械能守恒定律和速度关系求滑块P在位置B的速度,以及Q的速度.再对Q研究,由动能定理求出轻绳对滑块Q做功,等于轻绳对滑块P做功.由系统的机械能守恒分析P与Q的机械能之和如何变化.
解答 解:A、当滑块经过A、B两点时,弹簧对滑块的弹力大小相等,说明滑块P经过A点时,弹簧对P有向上的支持力,在B点时有向下的拉力.P在上滑的过程中,受到重力、轻绳的拉力、弹簧的弹力和杆的弹力,在A点时,合力向上,而在B点时合力向下,说明合力先向上后向下,则滑块P的速度先增大后减小,故A错误.
B、滑块P在位置B时Q的速度为0,由于滑块通过A、B两点时弹簧的弹性势能相等,由系统的机械能守恒得
Mg(L-Lcosθ)=mgLsinθ+$\frac{1}{2}m{v}_{P}^{2}$,又M=5m,解得 滑块P在位置B的速度为vB=$\sqrt{\frac{4}{5}gL}$,故B正确.
C、对Q研究,由动能定理得:Mg(L-Lcosθ)+WQ=0,则轻绳对滑块Q做功 WQ=-Mg(L-Lcosθ)=-5mgL(1-cos37°)=-mgL,所以轻绳对滑块P做功 WP=-WQ=mgL,故C正确.
D、对于弹簧、两个滑块组成的系统,由于只有重力和弹力做功,则系统的机械能守恒,由于 弹簧的弹性势能先减小后增大,可知,P与Q的机械能之和先增大后减小,故D正确.
故选:BCD
点评 解决本题的关键要明确滑块经过A、B两点时,弹簧对滑块的弹力大小相等,说明在这两个位置弹簧的弹性势能相等.要知道滑块P到达B点时Q的速度为0.

练习册系列答案
相关题目
19.一物体沿固定光滑斜面下滑,从斜面顶端下滑到底端的过程中( )
| A. | 斜面对物体支持力的冲量为零 | B. | 斜面对物体的支持力做功为零 | ||
| C. | 物体所受合外力的冲量为零 | D. | 物体动量的增量等于重力的冲量 |
20. 某学生用如图所示的装置开展探究实验,弹簧秤一端固定在墙壁上,另一端与小木块A相连,当用力加速抽出长木板B的过程中,观察到弹簧秤的示数为3.0N,若匀速抽出木板B,弹簧秤的示数( )
某学生用如图所示的装置开展探究实验,弹簧秤一端固定在墙壁上,另一端与小木块A相连,当用力加速抽出长木板B的过程中,观察到弹簧秤的示数为3.0N,若匀速抽出木板B,弹簧秤的示数( )
 某学生用如图所示的装置开展探究实验,弹簧秤一端固定在墙壁上,另一端与小木块A相连,当用力加速抽出长木板B的过程中,观察到弹簧秤的示数为3.0N,若匀速抽出木板B,弹簧秤的示数( )
某学生用如图所示的装置开展探究实验,弹簧秤一端固定在墙壁上,另一端与小木块A相连,当用力加速抽出长木板B的过程中,观察到弹簧秤的示数为3.0N,若匀速抽出木板B,弹簧秤的示数( )| A. | 一定大于3.0 N | B. | 一定小于3.0 N | C. | 一定等于3.0 N | D. | 一定为零 |
17. 一个均匀的透明圆柱体切成横截面如图所示的柱体,一束平行光从空气垂直AB平面射入(不考虑二次反射),则( )
一个均匀的透明圆柱体切成横截面如图所示的柱体,一束平行光从空气垂直AB平面射入(不考虑二次反射),则( )
 一个均匀的透明圆柱体切成横截面如图所示的柱体,一束平行光从空气垂直AB平面射入(不考虑二次反射),则( )
一个均匀的透明圆柱体切成横截面如图所示的柱体,一束平行光从空气垂直AB平面射入(不考虑二次反射),则( )| A. | II部分光线一定能全部射出 | |
| B. | II部分光线能否全部射出与透明体的折射率有关 | |
| C. | I、III两部分光线一定能全部射出 | |
| D. | I、III两部分光线能否全部射出与透明体的折射率有关 |
4. 如图所示,河水流动的速度为v且处处相同,河宽度为a,在船下水点A的下游距离为b处是瀑布,为了使小船渡河安全(不掉到瀑布里去且本题中小船速度均指静水中的速度)则下列说法正确的是( )
如图所示,河水流动的速度为v且处处相同,河宽度为a,在船下水点A的下游距离为b处是瀑布,为了使小船渡河安全(不掉到瀑布里去且本题中小船速度均指静水中的速度)则下列说法正确的是( )
 如图所示,河水流动的速度为v且处处相同,河宽度为a,在船下水点A的下游距离为b处是瀑布,为了使小船渡河安全(不掉到瀑布里去且本题中小船速度均指静水中的速度)则下列说法正确的是( )
如图所示,河水流动的速度为v且处处相同,河宽度为a,在船下水点A的下游距离为b处是瀑布,为了使小船渡河安全(不掉到瀑布里去且本题中小船速度均指静水中的速度)则下列说法正确的是( )| A. | 小船船头垂直河岸渡河时间最短,最短时间为t=$\frac{b}{v}$,此时小船速度最大,最大速度为vmax=$\frac{av}{b}$ | |
| B. | 小船轨迹沿y轴方向渡河,位移最小,速度最大,最大速度为vmax=$\frac{av}{b}$ | |
| C. | 小船沿轨迹AB运动,位移最长,时间最长,速度最小,最小速度vmin=$\frac{av}{b}$ | |
| D. | 小船沿轨迹AB运动,位移最大,速度最小,最小速度vmin=$\frac{av}{{\sqrt{{a^2}+{b^2}}}}$ |
14.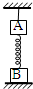 如图,A、B两物块质量分别为 2m和m,用一足够长的轻弹簧相连,将A用长度适当的轻绳悬于天花板上,系统处于静止状态,B物块恰好与水平桌面接触且无压力,此时轻弹簧的伸长量为x,重力加速度为g,现将悬绳剪断,下列说法正确的是( )
如图,A、B两物块质量分别为 2m和m,用一足够长的轻弹簧相连,将A用长度适当的轻绳悬于天花板上,系统处于静止状态,B物块恰好与水平桌面接触且无压力,此时轻弹簧的伸长量为x,重力加速度为g,现将悬绳剪断,下列说法正确的是( )
 如图,A、B两物块质量分别为 2m和m,用一足够长的轻弹簧相连,将A用长度适当的轻绳悬于天花板上,系统处于静止状态,B物块恰好与水平桌面接触且无压力,此时轻弹簧的伸长量为x,重力加速度为g,现将悬绳剪断,下列说法正确的是( )
如图,A、B两物块质量分别为 2m和m,用一足够长的轻弹簧相连,将A用长度适当的轻绳悬于天花板上,系统处于静止状态,B物块恰好与水平桌面接触且无压力,此时轻弹簧的伸长量为x,重力加速度为g,现将悬绳剪断,下列说法正确的是( )| A. | 悬绳剪断瞬间,A物块的加速度大小为 1.5g | |
| B. | 悬绳剪断瞬间,A物块的加速度大小为g | |
| C. | 悬绳剪断后,A物块向下运动距离x时速度最大 | |
| D. | 悬绳剪断后,A物块向下运动距离3x时速度最大 |
18.小明同学用玩具手枪研究平抛运动的规律.已知枪口离地面的高度为h1,枪口与竖直墙的距离为S,重力加速度为g,水平射出的子弹大在墙上的点离地面的高度为h2.则子弹射出时的初速度为( )
| A. | S$\sqrt{\frac{g}{2({h}_{1}-{h}_{2})}}$ | B. | S$\sqrt{\frac{g}{2{h}_{1}}}$ | C. | S$\sqrt{\frac{g}{2{h}_{2}}}$ | D. | S$\sqrt{\frac{2{h}_{1}}{g}}$ |
19.甲、乙两星球的平均密度相等,半径之比是R甲:R乙=4:1,则同一物体在这两个星球表面受到的重力之比是( )
| A. | 1:1 | B. | 4:1 | C. | 1:16 | D. | 1:64 |
 如图所示,物体的质量m=4kg,与水平面间的动摩擦因数为μ=0.2,在倾角为37°,P=20N的恒力作用下,由静止开始沿水平地面做加速度运动,(g=10m/s2,sin37°=0.6,cos37°=0.8).求:
如图所示,物体的质量m=4kg,与水平面间的动摩擦因数为μ=0.2,在倾角为37°,P=20N的恒力作用下,由静止开始沿水平地面做加速度运动,(g=10m/s2,sin37°=0.6,cos37°=0.8).求: