题目内容
2. 如图所示,在竖直平面内有一边界半径为R的圆形匀强磁场区域,磁感应强度为B,方向垂直纸面向里,一带负电的粒子(重力不计)从圆边缘的P点沿直径方向以初速度v进入匀强磁场中,射出磁场时速度方向偏转了60°,求:
如图所示,在竖直平面内有一边界半径为R的圆形匀强磁场区域,磁感应强度为B,方向垂直纸面向里,一带负电的粒子(重力不计)从圆边缘的P点沿直径方向以初速度v进入匀强磁场中,射出磁场时速度方向偏转了60°,求:(1)该粒子的荷质比$\frac{q}{m}$
(2)该粒子在磁场运动的时间t.
分析 (1)画出轨迹,由几何知识求出半径,根据牛顿第二定律求出荷质比.
(2)求出粒子运动的周期,再根据偏转角θ与时间的关系公式:t=$\frac{θ}{2π}$T求得粒子在磁场中运动的时间.
解答 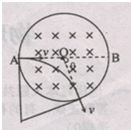 解:(1)画出粒子运动的轨迹如图,
解:(1)画出粒子运动的轨迹如图,
由几何知识得:
粒子运动的轨道半径 r=Rcot30°=$\sqrt{3}$R
粒子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,则得:
qvB=m$\frac{{v}^{2}}{r}$
联立解得:$\frac{q}{m}$=$\frac{v}{Br}$=$\frac{\sqrt{3}v}{3Br}$
(2)粒子在磁场中运动的周期为 T=$\frac{2πm}{qB}$
带电粒子速度的偏向角为θ=60°,其运动时间为 t=$\frac{θ}{360°}$T
可得 t=$\frac{\sqrt{3}πR}{3v}$
答:
(1)该粒子的荷质比$\frac{q}{m}$为$\frac{\sqrt{3}v}{3Br}$.
(2)该粒子在磁场运动的时间t为$\frac{\sqrt{3}πR}{3v}$.
点评 本题是粒子在磁场中圆周运动的轨迹问题,关键是运用几何知识画出轨迹、求出半径.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
13.真空中两个静止的点电荷,相距为r时相互作用的库仑力大小为F,现不改变它们的电荷量,使它们之间的距离为2r,则库仑力大小变为( )
| A. | $\frac{1}{4}$F | B. | $\frac{1}{2}$F | C. | 2F | D. | 4F |
17. 将阻值为5Ω的电阻接到内阻不计的交流电源上,电源电动势随时间变化的规律如图所示,下列说法正确的是( )
将阻值为5Ω的电阻接到内阻不计的交流电源上,电源电动势随时间变化的规律如图所示,下列说法正确的是( )
 将阻值为5Ω的电阻接到内阻不计的交流电源上,电源电动势随时间变化的规律如图所示,下列说法正确的是( )
将阻值为5Ω的电阻接到内阻不计的交流电源上,电源电动势随时间变化的规律如图所示,下列说法正确的是( )| A. | 电路中交变电流的频率为0.25Hz | |
| B. | 通过电阻的电流为$\sqrt{2}$A | |
| C. | 电阻消耗的电功率为2.5W | |
| D. | 用交流电压表测得电阻两端的电压是5V |
7.洛伦兹力演示仪是由励磁线圈(也叫亥姆霍兹线圈)、洛伦兹力管和电源控制部分组成的.励磁线圈是一对彼此平行的共轴串联的圆形线圈,它能够在两线圈之间产生(垂直于线圈平面的)匀强磁场.洛伦兹力管的圆球形玻璃泡内有电子枪,能够连续发射出电子,玻璃泡内充满稀薄气体,电子在玻璃泡内运动时,可以显示出电子运动的径迹.其结构如图所示.现给励磁线圈通电,电子枪垂直磁场方向向左发射电子,恰好形成如“结构示意图”所示的圆形径迹,则( )


| A. | 励磁线圈通有逆时针方向的电流 | |
| B. | 若只增大加速电压,可以使电子流的圆形径迹半径增大 | |
| C. | 若只增大励磁线圈中的电流,可以使电子流的圆形径迹半径增大 | |
| D. | 若已知电子的比荷,灯丝发出的电子的初速为零,加速电压为U,则可通过测量圆形径迹的直径来估算两线圈的磁感应强度 |
14.如图所示,物体与粗糙斜面一起沿水平面向左匀速运动.则斜面对物体的作用力方向( )


| A. | 必沿b方向 | B. | 必沿d方向 | ||
| C. | 必沿c方向 | D. | a、b、c、d方向都有可能 |
11. 如图所示,吊环比赛中选手先双手抓住吊环,双臂缓慢张开到图示位置后保持静止,此时连接吊环的两根绳索与竖直方向的夹角均为θ.已知选手的体重为G,吊环和绳索的重力不计.则每条绳索的张力为( )
如图所示,吊环比赛中选手先双手抓住吊环,双臂缓慢张开到图示位置后保持静止,此时连接吊环的两根绳索与竖直方向的夹角均为θ.已知选手的体重为G,吊环和绳索的重力不计.则每条绳索的张力为( )
 如图所示,吊环比赛中选手先双手抓住吊环,双臂缓慢张开到图示位置后保持静止,此时连接吊环的两根绳索与竖直方向的夹角均为θ.已知选手的体重为G,吊环和绳索的重力不计.则每条绳索的张力为( )
如图所示,吊环比赛中选手先双手抓住吊环,双臂缓慢张开到图示位置后保持静止,此时连接吊环的两根绳索与竖直方向的夹角均为θ.已知选手的体重为G,吊环和绳索的重力不计.则每条绳索的张力为( )| A. | $\frac{G}{2}$sinθ | B. | $\frac{G}{2}$cosθ | C. | $\frac{G}{2sinθ}$ | D. | $\frac{G}{2cosθ}$ |




