题目内容
14.蹦床运动中运动员在一张绷紧的弹性网上蹦起、腾空并做空中动作.若一位蹦床运动员仅在竖直方向上运动,弹簧床对运动员的弹力F随时间t的变化规律通过传感器用计算机绘制出来,如图所示.由图象可知,运动过程中,运动员最大加速度am及离开蹦床上升的最大高度h(不计空气阻力,g取10m/s2)为( )
| A. | am=40m/s2 h=3.2m | B. | am=40m/s2 h=3.0m | ||
| C. | am=20m/s2 h=3.2m | D. | am=20m/s2 h=3.0m |
分析 当弹力最大时,运动员的加速度.由图读出最大的弹力为2500N,根据牛顿第二定律求出最大加速度;由图读出运动员在空中运动的时间,由竖直上抛的规律求出最大高度.
解答 解:运动员陷落最深时由图可知:${F}_{m}^{\;}=2500N$
根据牛顿第二定律:${F}_{m}^{\;}-mg=m{a}_{m}^{\;}$,可得最大加速度${a}_{m}^{\;}=\frac{F}{m}-g=\frac{2500}{50}-10=40m/{s}_{\;}^{2}$
运动员在空中运动时间:t=11-9.4=1.6s
上升到最高点的时间t′=0.8s
离开蹦床上升的最大高度$h=\frac{1}{2}gt{′}_{\;}^{2}=\frac{1}{2}×10×0.{8}_{\;}^{2}=3.2m$
故选:A
点评 本题要读懂图象,由图象读出运动员在空中运动的时间t,二要将运动员的运动近似看成竖直上抛,根据对称性求解最大高度.

练习册系列答案
相关题目
4.某振动系统的固有频率为f0,在周期性驱动力的作用下做受迫振动,驱动力的频率为f,若驱动力的振幅保持不变,下列说法正确的是( )
| A. | 当f<f0时,该振动系统的振幅随f增大而减小 | |
| B. | 当f>f0时,该振动系统的振幅随f减小而增大 | |
| C. | 该振动系统的振动稳定后,振动的频率等于f0 | |
| D. | 该振动系统的振动稳定后,振动的频率等于f0的整数倍 |
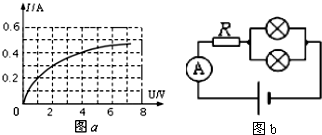
9.小郑同学研究额定电压为4.5v的玩具电动机M的伏安特性曲线,所用电压表内阻约为5千欧,电流内阻约为3欧.如图是他设计的四个实验电路图.

(1)应该选用丙电路图(填代号甲、乙、丙、丁)
(2)该同学实验记录数据如下表格:
根据表格数据,该同学在坐标纸上画出两条不相连的伏安特性曲线.为确定一条曲线的终点、另一条曲的终起点,该同学继续做实验,他该这样操作:控制电压约为0.8V,缓慢调节滑动变阻器,找出电动机刚好转动时的电压和电流; 然后将电压调至4.5V,读出电流值
(3)根据实验数据,玩具电动机的内阻为2.0Ω(保留两位有效数字)
(4)当玩具电动机得到4.00v的电压时,输出功率为1.65 W(保留三位有效数字)
(5)在表格记录的数据范围内,当玩具电动机对外输出功率时,电动机的效率随工作电压的增大而增大(填“增大”或“不变”或“减小”)

(1)应该选用丙电路图(填代号甲、乙、丙、丁)
(2)该同学实验记录数据如下表格:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 电压U/V | 0.20 | 0.40 | 0.60 | 0.80 | 1.20 | 1.60 | 2.00 | 2.40 | 2.80 | 3.20 | 3.60 | 4.00 |
| 电流I/A | 0.10 | 0.20 | 0.30 | 0.38 | 0.20 | 0.26 | 0.32 | 0.38 | 0.44 | 0.50 | 0.54 | 0.58 |
| 电机状态 | 不转 | 不转 | 不转 | 不转 | 转动 | 转动 | 转动 | 转动 | 转动 | 转动 | 转动 | 转动 |
(3)根据实验数据,玩具电动机的内阻为2.0Ω(保留两位有效数字)
(4)当玩具电动机得到4.00v的电压时,输出功率为1.65 W(保留三位有效数字)
(5)在表格记录的数据范围内,当玩具电动机对外输出功率时,电动机的效率随工作电压的增大而增大(填“增大”或“不变”或“减小”)
6.马航失联牵动全世界人的心,初步确定失事地点位于南纬30○ 52′.东经115○ 52′的澳大利亚西南城市珀斯附近的海域.有一颗绕地球做匀速圆周运动的卫星,每天上午同一时刻在该区域的正上方对海面拍照,则( )
| A. | 该卫星可能是通过地球两极上方的轨道 | |
| B. | 该卫星平面可能与南纬30○ 52′所确定的平面共面 | |
| C. | 该卫星平面一定与东经115○ 52′所确定的平面共面 | |
| D. | 地球自转周期一定是该卫星运行周期的整数倍 |
14. 质量为m的小球,用长为L的轻绳悬于O点,小球在水平力F的作用下,从最低点P缓慢地移动到Q点,这时绳与竖直方向成θ角,如图所示.这一过程中小球的受力情况及力F做的功分别是( )
质量为m的小球,用长为L的轻绳悬于O点,小球在水平力F的作用下,从最低点P缓慢地移动到Q点,这时绳与竖直方向成θ角,如图所示.这一过程中小球的受力情况及力F做的功分别是( )
 质量为m的小球,用长为L的轻绳悬于O点,小球在水平力F的作用下,从最低点P缓慢地移动到Q点,这时绳与竖直方向成θ角,如图所示.这一过程中小球的受力情况及力F做的功分别是( )
质量为m的小球,用长为L的轻绳悬于O点,小球在水平力F的作用下,从最低点P缓慢地移动到Q点,这时绳与竖直方向成θ角,如图所示.这一过程中小球的受力情况及力F做的功分别是( )| A. | 小球受力平衡,mgLcosθ | B. | 小球受力不平衡,FLcosθ | ||
| C. | 小球受力不平衡,FLsinθ | D. | 小球受力平衡,mgL(1-cosθ) |

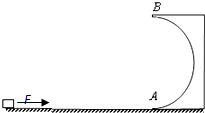 半径为R=0.9m的光滑半圆形轨道固定在水平地面上,与水平面相切于A点,在距离A点1.3m处有一可视为质点的小滑块,质量为m=0.5kg,小滑块与水平面间的动摩擦因数为u=0.2,施加一个大小为F=11N的水平推力,运动到A点撤去推力,滑块从圆轨道最低点A处冲上竖直轨道.(g=10m/s2)问:
半径为R=0.9m的光滑半圆形轨道固定在水平地面上,与水平面相切于A点,在距离A点1.3m处有一可视为质点的小滑块,质量为m=0.5kg,小滑块与水平面间的动摩擦因数为u=0.2,施加一个大小为F=11N的水平推力,运动到A点撤去推力,滑块从圆轨道最低点A处冲上竖直轨道.(g=10m/s2)问: