题目内容
17. 如图甲所示,两块相同的平行金属板M、N正对着放置,相距为$\frac{R}{2}$,板M、N上的小孔A、C与O三点共线,CO=R,连线AO垂直于板M、N.以O为圆心、R为半径的圆形区域内存在磁感应强度大小为B、方向垂直纸面向里的匀强磁场.收集屏PQ上各点到O点的距离都为2R,两端点P、Q关于连线AO对称,屏PQ所对的圆心角θ=120°.质量为m、电荷量为e的质子连续不断地经A进入M、N间的电场,接着通过C进入磁场.质子重力及质子间的相互作用均不计,质子在A处的速度看作零.
如图甲所示,两块相同的平行金属板M、N正对着放置,相距为$\frac{R}{2}$,板M、N上的小孔A、C与O三点共线,CO=R,连线AO垂直于板M、N.以O为圆心、R为半径的圆形区域内存在磁感应强度大小为B、方向垂直纸面向里的匀强磁场.收集屏PQ上各点到O点的距离都为2R,两端点P、Q关于连线AO对称,屏PQ所对的圆心角θ=120°.质量为m、电荷量为e的质子连续不断地经A进入M、N间的电场,接着通过C进入磁场.质子重力及质子间的相互作用均不计,质子在A处的速度看作零.(1)若M、N间的电压UMN=+U时,求质子进入磁场时速度的大小v0.
(2)若M、N间接入如图乙所示的随时间t变化的电压UMN=|U0sin$\frac{π}{T}$t|(式中U0=$\frac{3e{B}^{2}{R}^{2}}{m}$,周期T已知),且在质子通过板间电场区域的极短时间内板间电场视为恒定,则质子在哪些时刻自s1处进入板间,穿出磁场后均能打到收集屏PQ上?
(3)在上述(2)问的情形下,当M、N间的电压不同时,质子从s1处到打在收集屏PQ上经历的时间t会不同,求t的最大值.
分析 (1)质子在电场中做加速运动,由动能定理可求得质子进入磁场时的速度;
(2)由动能定理可得出质子进入磁场时的速度表达式;由几何关系可知质子能打在收集屏上的临界条件,则由牛顿第二定律可求得能打在屏上的质子进入电场的时刻;
(3)根据质子在电场与磁场中运动的关系可推导出质子运动的最大时间.
解答 解:(1)根据动能定理,有:$eU=\frac{1}{2}m{v}_{0}^{2}-0$
解得:${v}_{0}^{\;}=\sqrt{\frac{2eU}{m}}$
(2)质子在板间运动,根据动能定理,有$e{U}_{MN}^{\;}=\frac{1}{2}m{v}_{\;}^{2}-0$
质子在磁场中运动,根据牛顿第二定律,有:$evB=m\frac{{v}_{\;}^{2}}{r}$
若质子能打在收集屏,轨道半径r与R应满足的关系:
$r≥\sqrt{3}R$
解得板间电压:${U}_{MN}^{\;}≥\frac{3e{B}_{\;}^{2}{R}_{\;}^{2}}{2m}$
结合图象可知:质子在$t=kT+\frac{T}{6}~kT+\frac{5T}{6}(k=0、1、2…)$之间任一时刻从${S}_{1}^{\;}$处进入电场,均能打到收集屏上
(3)M、N间的电压越小,质子穿出电场进入磁场时的速度越小,质子在极板间经历的时间越长,同时在磁场中运动轨迹的半径越小,在磁场中经历的时间也会越长,出磁场后打到收集屏前作匀速运动的时间也越长,所以当质子打在收集屏的P端时,对应时间t最长,两板间的电压此时为:
${U}_{MN}^{\;}=\frac{1}{2}{U}_{0}^{\;}$
在板间电场中运动时间:${t}_{1}^{\;}=\frac{R}{v}$
在磁场中运动时间:${t}_{2}^{\;}=\frac{60°}{360°}×\frac{2πr}{v}=\frac{π\sqrt{3}R}{3v}$
出磁场后打到收集屏前作匀速运动的时间:${t}_{3}^{\;}=\frac{R}{v}$
所以,运动总时间为:
$t={t}_{1}^{\;}+{t}_{2}^{\;}+{t}_{3}^{\;}$=$(\frac{2}{\sqrt{3}}+\frac{π}{3})\frac{\sqrt{3}R}{v}$=$(\frac{2}{\sqrt{3}}+\frac{π}{3})\frac{m}{eB}$
答:(1)质子进入磁场时速度的大小为$\sqrt{\frac{2eU}{m}}$
(2)质子在$t=kT+\frac{T}{6}~kT+\frac{5T}{6}(k=0、1、2…)$之间任一时刻从${S}_{1}^{\;}$处进入电场均能打到收集屏上
(3)时间t的最大值为$(\frac{2}{\sqrt{3}}+\frac{π}{3})\frac{m}{eB}$
点评 本题要注意质子在电场中加速后进入磁场中偏转;加速电场中由动能定理求出速度,而在磁场中的运动要由几何关系确定圆心和半径,再根据牛顿第二定律及向心力公式列式求解.本题中的难点在于找出时间范围及时间的最大值.

 甲、乙两物体沿同一方向做直线运动,6s末在途中相遇,它们的速度图象如图所示,可以确定( )
甲、乙两物体沿同一方向做直线运动,6s末在途中相遇,它们的速度图象如图所示,可以确定( )| A. | t=0时甲在乙的前方27m处 | B. | t=0时乙在甲的前方27m处 | ||
| C. | t=6s时,甲的速度大于乙的速度 | D. | t=6s之后两物体不会再相遇 |
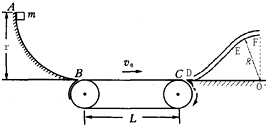 如图所示,一半径r=0.2m的$\frac{1}{4}$光滑圆弧形槽底B与水平传送带相接,传送带的运行速度为v0=4m/s,长为L=1.25m,滑块与传送带间的动摩擦因数μ=0.2,DEF为固定于竖直平面内的一段内壁光滑的中空方形细管,EF段被弯成以O为圆心,半径R=0.25m的一小段圆弧,管的D端弯成与水平传带C端平滑相接,O点位于地面,OF连线竖直,一质量为M=0.2kg的滑块a从圆弧顶端A点无初速滑下,滑到传送带上后做匀加速运动,过后滑块被传送带送入管DEF,已知a滑块可视为质点,a横截面略小于管中空部分的横截面,重力加速度g取10m/s2.求:
如图所示,一半径r=0.2m的$\frac{1}{4}$光滑圆弧形槽底B与水平传送带相接,传送带的运行速度为v0=4m/s,长为L=1.25m,滑块与传送带间的动摩擦因数μ=0.2,DEF为固定于竖直平面内的一段内壁光滑的中空方形细管,EF段被弯成以O为圆心,半径R=0.25m的一小段圆弧,管的D端弯成与水平传带C端平滑相接,O点位于地面,OF连线竖直,一质量为M=0.2kg的滑块a从圆弧顶端A点无初速滑下,滑到传送带上后做匀加速运动,过后滑块被传送带送入管DEF,已知a滑块可视为质点,a横截面略小于管中空部分的横截面,重力加速度g取10m/s2.求:

 如图所示,飞机在竖直平面内俯冲又拉起,这一过程可看做圆周运动,在最低点飞行员对座椅的压力大小为F,设飞行员所受重力为G,则飞机在经过最低点时,比较两力的大小得( )
如图所示,飞机在竖直平面内俯冲又拉起,这一过程可看做圆周运动,在最低点飞行员对座椅的压力大小为F,设飞行员所受重力为G,则飞机在经过最低点时,比较两力的大小得( )
 如图所示,水平面上固定一倾斜角为37°的粗糙斜面,紧靠斜面底端有一质量为M=4kg的木板,木板与斜面底端之间通过微小弧形轨道相接,以保证滑块从斜面滑到木板的速度大小不变.质量为m=2kg的滑块从斜面上高h=5m处由静止滑下,到达斜面底端的速度为v0=6m/s,并以此速度滑上木板左端,最终滑块没有从木板上滑下.已知滑块与木板间的动摩擦因数μ1=0.25,木板与地面间的动摩擦因数μ2=0.1,取g=10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,水平面上固定一倾斜角为37°的粗糙斜面,紧靠斜面底端有一质量为M=4kg的木板,木板与斜面底端之间通过微小弧形轨道相接,以保证滑块从斜面滑到木板的速度大小不变.质量为m=2kg的滑块从斜面上高h=5m处由静止滑下,到达斜面底端的速度为v0=6m/s,并以此速度滑上木板左端,最终滑块没有从木板上滑下.已知滑块与木板间的动摩擦因数μ1=0.25,木板与地面间的动摩擦因数μ2=0.1,取g=10m/s2,sin37°=0.6,cos37°=0.8.求: