题目内容
13. 如图所示,一个固定在竖直平面上的光滑半圆形管道,管道里有一个直径略小于管道内径的小球,小球在管道内做圆周运动,从B点脱离后做平抛运动,经过0.3秒后又恰好垂直与倾角为45°的斜面相碰到.已知圆轨道半径为R=1m,小球的质量为m=1kg,g取10m/s2.求
如图所示,一个固定在竖直平面上的光滑半圆形管道,管道里有一个直径略小于管道内径的小球,小球在管道内做圆周运动,从B点脱离后做平抛运动,经过0.3秒后又恰好垂直与倾角为45°的斜面相碰到.已知圆轨道半径为R=1m,小球的质量为m=1kg,g取10m/s2.求(1)小球在斜面上的相碰点C与B点的水平距离
(2)小球经过圆弧轨道的B点时,受到轨道的作用力NB的大小和方向?
(3)小球经过圆弧轨道的A点时的速率.
分析 (1)小球恰好垂直与倾角为450的斜面相碰到,说明小球在C点竖直方向的分速度和水平分速度相等,代人公式即可;
(2)小球经过圆弧轨道的B点时,做圆周运动,所受轨道作用力与重力一起提供向心力.
(3)小球从A到B的过程中的机械能守恒,由此即可求出A点的速率.
解答 解:(1)根据平抛运动的规律和运动合成的可知:
$tan45°=\frac{{v}_{y}}{{v}_{x}}$
则小球在C点竖直方向的分速度和水平分速度相等,得:vx=vy=gt=3m/s,
则B点与C点的水平距离为:
x=vxt=0.9m
(2)根据牛顿运动定律,在B点(设轨道对球的作用力方向向下)
${N}_{B}+mg=\frac{m{v}_{B}^{2}}{R}$,
解得:NB=-1N 负号表示轨道对球的作用力方向向上
(3)小球从A到B的过程中机械能守恒,得:
$\frac{1}{2}m{v}_{A}^{2}=mg•2R+\frac{1}{2}m{v}_{B}^{2}$
代入数据得:vA=7m/s
答:(1)小球在斜面上的相碰点C与B点的水平距离是0.9m;
(2)小球经过圆弧轨道的B点时,所受轨道作用力NB的大小1N,方向竖直向上.
(3)小球经过圆弧轨道的A点时的速率是7m/s.
点评 该题考查竖直平面内的圆周运动与平抛运动,小球恰好垂直与倾角为45°的斜面相碰到是解题的关键,要正确理解它的含义.

练习册系列答案
相关题目
3.下列说法中正确的是( )
| A. | 不可能从单一热源吸收能量,使之完全变成功,而不产生其他影响 | |
| B. | 农民锄松土壤,是为了破坏土壤里的毛细管,保存土壤里的水分 | |
| C. | 随着分子间距增大,分子间的引力和斥力都减小,但斥力减小更快,合力表现为引力 | |
| D. | 温度升高,每个分子热运动的动能越大 | |
| E. | 对某种气体而言,已知阿伏伽德罗常数、气体的摩尔质量和密度,可计算出该种气体分子间的平均距离 |
1.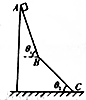 如图所示,AB与BC是两个场地相同的斜面,但倾角不同,AB与水平方向夹角为θ1,BC与水平方向夹角为θ2,两斜面间用光滑的小圆弧连接,物体通过时无能量损失,一物块从A点由静止释放,运动到C点速度刚好为0.已知物块与两斜面的动摩擦因数相同,则物块与两斜面的动摩擦因数为( )
如图所示,AB与BC是两个场地相同的斜面,但倾角不同,AB与水平方向夹角为θ1,BC与水平方向夹角为θ2,两斜面间用光滑的小圆弧连接,物体通过时无能量损失,一物块从A点由静止释放,运动到C点速度刚好为0.已知物块与两斜面的动摩擦因数相同,则物块与两斜面的动摩擦因数为( )
 如图所示,AB与BC是两个场地相同的斜面,但倾角不同,AB与水平方向夹角为θ1,BC与水平方向夹角为θ2,两斜面间用光滑的小圆弧连接,物体通过时无能量损失,一物块从A点由静止释放,运动到C点速度刚好为0.已知物块与两斜面的动摩擦因数相同,则物块与两斜面的动摩擦因数为( )
如图所示,AB与BC是两个场地相同的斜面,但倾角不同,AB与水平方向夹角为θ1,BC与水平方向夹角为θ2,两斜面间用光滑的小圆弧连接,物体通过时无能量损失,一物块从A点由静止释放,运动到C点速度刚好为0.已知物块与两斜面的动摩擦因数相同,则物块与两斜面的动摩擦因数为( )| A. | $\frac{2}{cos{θ}_{1}+cot{θ}_{2}}$ | B. | $\frac{cos{θ}_{1}+cos{θ}_{2}}{sin{θ}_{1}+sin{θ}_{2}}$ | ||
| C. | $\frac{sin{θ}_{1}-sin{θ}_{2}}{cos{θ}_{1}-cos{θ}_{2}}$ | D. | $\frac{sin{θ}_{1}+sin{θ}_{2}}{cos{θ}_{1}+cos{θ}_{2}}$ |
8.对于做匀速圆周运动的物体,下列说法中正确的是( )
| A. | 其角速度不变 | B. | 其向心加速度不变 | ||
| C. | 其线速度不变 | D. | 其所受合力不变 |
18. 如图所示,一细木棍AB斜靠在地面与竖直墙壁之间,木棍AB与水平面之间的夹角为45°,A点到地面的距离为1m,已知重力加速度为10m/s2.空气阻力不计,从竖直墙上距离地面0.8m的C点水平射出速度大小不同的弹丸,以A为原点,AB为x轴正方向,则弹丸射中x轴的范围( )
如图所示,一细木棍AB斜靠在地面与竖直墙壁之间,木棍AB与水平面之间的夹角为45°,A点到地面的距离为1m,已知重力加速度为10m/s2.空气阻力不计,从竖直墙上距离地面0.8m的C点水平射出速度大小不同的弹丸,以A为原点,AB为x轴正方向,则弹丸射中x轴的范围( )
 如图所示,一细木棍AB斜靠在地面与竖直墙壁之间,木棍AB与水平面之间的夹角为45°,A点到地面的距离为1m,已知重力加速度为10m/s2.空气阻力不计,从竖直墙上距离地面0.8m的C点水平射出速度大小不同的弹丸,以A为原点,AB为x轴正方向,则弹丸射中x轴的范围( )
如图所示,一细木棍AB斜靠在地面与竖直墙壁之间,木棍AB与水平面之间的夹角为45°,A点到地面的距离为1m,已知重力加速度为10m/s2.空气阻力不计,从竖直墙上距离地面0.8m的C点水平射出速度大小不同的弹丸,以A为原点,AB为x轴正方向,则弹丸射中x轴的范围( )| A. | 0.2m<x<0.4m | B. | 0.2$\sqrt{2}$m<x<1.0m | C. | 0.2$\sqrt{2}$m<x<0.4$\sqrt{2}$m | D. | 0.2$\sqrt{2}$m<x<0.8$\sqrt{2}$m |
5. 垂直纸面匀强磁场O点静止放着一个放射性原子核,它发生衰变后粒子和反冲核轨迹如图所示,由图可以判断( )
垂直纸面匀强磁场O点静止放着一个放射性原子核,它发生衰变后粒子和反冲核轨迹如图所示,由图可以判断( )
 垂直纸面匀强磁场O点静止放着一个放射性原子核,它发生衰变后粒子和反冲核轨迹如图所示,由图可以判断( )
垂直纸面匀强磁场O点静止放着一个放射性原子核,它发生衰变后粒子和反冲核轨迹如图所示,由图可以判断( )| A. | 这是α衰变 | B. | 这是β衰变 | ||
| C. | 轨迹a是顺时针方向 | D. | 轨迹b是顺时针方向 |
2.下列关于物理量,物理量单位,物理意义的说法正确的是( )
| A. | 加速度是描述速度变化的物理量 | |
| B. | 使质量为1千克的物体产生1米每二次方秒的加速度的力就是1牛顿 | |
| C. | 在力学范围内,国际单位制中的基本单位是:米,秒,焦耳 | |
| D. | 物理量是标量的,一定没有方向 |
12. 电熨斗中装有双金属片温度传感器,这种双金属片的作用是控制电路的通断,如图所示为电熨斗的结构图,下列说法正确的是( )
电熨斗中装有双金属片温度传感器,这种双金属片的作用是控制电路的通断,如图所示为电熨斗的结构图,下列说法正确的是( )
 电熨斗中装有双金属片温度传感器,这种双金属片的作用是控制电路的通断,如图所示为电熨斗的结构图,下列说法正确的是( )
电熨斗中装有双金属片温度传感器,这种双金属片的作用是控制电路的通断,如图所示为电熨斗的结构图,下列说法正确的是( )| A. | 常温下,上、下触点是接触的 | |
| B. | 当温度过高时双金属片将发生形变使触点分离 | |
| C. | 双金属片下层金属热膨胀系数较大 | |
| D. | 若旋钮调温旋钮,使升降螺丝向下移动,则熨烫设置温度会更低 |