题目内容
16. 如图所示,轻质弹簧两端与质量分别为m1=1kg、m2=2kg的物块P、Q连在一起,将P、Q放在光滑的水平面上,靠墙、弹簧自然伸长时P静止在A点,用水平力F推P使弹簧压缩一段距离后静止,此过程中F做功4.5J,则撤去F后,求:
如图所示,轻质弹簧两端与质量分别为m1=1kg、m2=2kg的物块P、Q连在一起,将P、Q放在光滑的水平面上,靠墙、弹簧自然伸长时P静止在A点,用水平力F推P使弹簧压缩一段距离后静止,此过程中F做功4.5J,则撤去F后,求:(1)P在运动中的最大速度;
(2)Q运动后弹簧弹性势能的最大值;
(3)Q在运动中的最大速度;
(4)P通过A点后速度最小时弹簧的弹性势能.
分析 (1)用水平力F推P使弹簧压缩的过程中,弹簧的弹性势能增加,当撤去F后,弹簧的弹性势能转化为P的动能,弹簧刚恢复原长时,P的速度最大,由能量守恒定律求解.
(2)Q离开墙壁后,弹簧伸长,Q加速,P减速,当两者速度相等时,弹簧的伸长量最大,弹性势能最大.根据动量守恒和机械能守恒结合求解.
(3)当Q离开墙壁后弹簧第一次恢复原长时,Q的速度最大.根据系统的动量守恒和机械能守恒结合求解.
(4)根据当Q离开墙壁后弹簧第一次恢复原长时P的速度,分析P速度的最小值,再由系统的动量守恒和机械能守恒结合求解.
解答 解:(1)当Q刚离墙壁时,P的速度最大.设为vm.根据功能关系得:
$\frac{1}{2}{m}_{1}{v}_{m}^{2}$=WF;
可得 vm=$\sqrt{\frac{2{W}_{F}}{{m}_{1}}}$=$\sqrt{\frac{2×4.5}{1}}$=3m/s
(2)Q离开墙壁后,当两者速度相等时,弹簧的伸长量最大,弹性势能最大.取向左为正方向,根据动量守恒定律和机械能守恒定律得:
m1vm=(m1+m2)v;
$\frac{1}{2}$m1vm2=$\frac{1}{2}$(m1+m2)v2+Ep;
联立解得:P、Q的共同速度 v=1m/s.弹簧弹性势能的最大值 Ep=3J;
(3)当Q离开墙壁后弹簧第一次恢复原长时,Q的速度最大.根据系统的动量守恒得:
m1vm=m1v1+m2v2,
由机械能守恒定律得:
$\frac{1}{2}$m1vm2=$\frac{1}{2}$m1v12+$\frac{1}{2}$m2v22;
联立解得:Q在运动中的最大速度 v2=4m/s,此时P的速度 v1=-1m/s,负号表示方向向右.
(4)Q刚离开墙壁时P的速度为vm=3m/s,方向向左.Q离开墙壁后弹簧第一次恢复原长时,P的速度为v1=-1m/s,方向向右,所以P的速度最小为0.
设此时Q的速度为v3.弹簧的弹性势能为 Ep′.
根据动量守恒定律和机械能守恒定律得:
m1vm=m2v3;
$\frac{1}{2}$m1vm2=$\frac{1}{2}$m2v32+Ep′;
联立解得 Ep′=2.25J
答:
(1)P在运动中的最大速度是3m/s;
(2)Q运动后弹簧弹性势能的最大值是3J;
(3)Q在运动中的最大速度是4m/s;
(4)P通过A点后速度最小时弹簧的弹性势能是2.25J.
点评 解决本题首先要明确研究的过程,其次把握信隐含的条件:弹簧伸长最长时两木块的速度相同.知道Q离开墙壁后系统遵守两大守恒:动量守恒和机械能守恒,要注意选取正方向.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
| A. | 卡文迪许通过扭秤实验,测出了万有引力常量 | |
| B. | 奥斯特通过实验研究,发现了电流周围存在磁场 | |
| C. | 密立根通过实验研究,测出了元电荷的数值 | |
| D. | 牛顿根据理想斜面实验,提出力不是维持物体运动的原因 |
 一个带电荷量为-q、质量为m的小球从光滑绝缘的斜面轨道的A点由静止下滑,小球恰能通过半径为R的竖直圆形轨道的最高点B而做圆周运动.现在竖直方向上加如图所示的匀强电场,且电场强度满足mg=2qE.若仍从A点由静止释放该小球,则( )
一个带电荷量为-q、质量为m的小球从光滑绝缘的斜面轨道的A点由静止下滑,小球恰能通过半径为R的竖直圆形轨道的最高点B而做圆周运动.现在竖直方向上加如图所示的匀强电场,且电场强度满足mg=2qE.若仍从A点由静止释放该小球,则( )| A. | 小球仍恰好过B点 | |
| B. | 小球不能过B点 | |
| C. | 小球能过B点,且在B点与轨道之间压力不为0 | |
| D. | 以上说法都不对 |

 某同学测量玻璃砖的折射率,准备了下列器材:激光笔、直尺、刻度尺、一面镀有反射膜的平行玻璃砖.如图所示,直尺与玻璃砖平行放置,激光笔发出的一束激光从直尺上O点射向玻璃砖表面,在直尺上观察到A、B两个光点,读出OA间的距离为x1,AB间的距离为x2,测得图中直尺到玻璃砖上表面距离d1,玻璃砖厚度d2,则可计算出玻璃的折射率n.如果增大激光束与玻璃砖表面的夹角,则所测量得的折射率不变(选填“增大”、“不变”或“减小”).如果实验室有厚度为d2、d3的两块玻璃砖,已知d2<d3,为减小测量误差,可选择厚度为d3(选填“d2”或“d3”)的玻璃砖.
某同学测量玻璃砖的折射率,准备了下列器材:激光笔、直尺、刻度尺、一面镀有反射膜的平行玻璃砖.如图所示,直尺与玻璃砖平行放置,激光笔发出的一束激光从直尺上O点射向玻璃砖表面,在直尺上观察到A、B两个光点,读出OA间的距离为x1,AB间的距离为x2,测得图中直尺到玻璃砖上表面距离d1,玻璃砖厚度d2,则可计算出玻璃的折射率n.如果增大激光束与玻璃砖表面的夹角,则所测量得的折射率不变(选填“增大”、“不变”或“减小”).如果实验室有厚度为d2、d3的两块玻璃砖,已知d2<d3,为减小测量误差,可选择厚度为d3(选填“d2”或“d3”)的玻璃砖.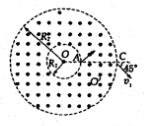 如图所示,在以O为圆心,内外半径分别为R1和R2的圆环区域内,存在垂直纸面的匀强磁场,R1=R0,R2=3R0,一电荷量为+q,质量为m的粒子从内圆上的A点进入该区域,不计重力.
如图所示,在以O为圆心,内外半径分别为R1和R2的圆环区域内,存在垂直纸面的匀强磁场,R1=R0,R2=3R0,一电荷量为+q,质量为m的粒子从内圆上的A点进入该区域,不计重力.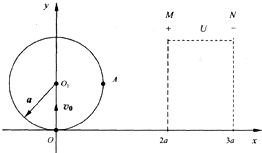 如图所示,在坐标系xOy内有一半径为d的圆形区域,圆心坐标为O1(0,a),圆内分布有垂直纸面向里的匀强磁场.在M、N之间的矩形区域(即x=2a,x=3a和y=0,y=2a所围成的区域)内有一沿+x方向的匀强电场.一质量为m、电荷量为-q(q>0)的粒子以速度v0从O点垂直于磁场沿+y轴方向射入,粒子恰好从A点射出磁场,A、O1两点的连线与x轴平行.(不计粒子重力)
如图所示,在坐标系xOy内有一半径为d的圆形区域,圆心坐标为O1(0,a),圆内分布有垂直纸面向里的匀强磁场.在M、N之间的矩形区域(即x=2a,x=3a和y=0,y=2a所围成的区域)内有一沿+x方向的匀强电场.一质量为m、电荷量为-q(q>0)的粒子以速度v0从O点垂直于磁场沿+y轴方向射入,粒子恰好从A点射出磁场,A、O1两点的连线与x轴平行.(不计粒子重力)