题目内容
17.如图所示,在绝缘水平面上,相隔为2L的AB两点分别固定有两个电量均为Q的正点电荷,a,O,b是AB连线的三点,且O为中点,Oa=Ob=$\frac{L}{2}$.一质量为m、电量为q的小滑块以初速度v0从a点出发,沿直线AB向B点运动,在运动过程中电荷量受到大小恒定的摩擦阻力作用,当它第一次运动到O点时速度为2v0,继续运动到b点时的速度刚好为零,经多次往返后,滑块停于某点,已知静电力常量为k,下列说法正确的是( )
| A. | 滑块一定停于O点 | |
| B. | 滑块在a点受到的电场力大小为$\frac{40kQq}{9{L}^{2}}$ | |
| C. | aO两点间的电势差为$\frac{7m{v}_{0}^{2}}{4q}$ | |
| D. | 运动过程中滑块受到的摩擦阻力大小为$\frac{m{v}_{0}^{2}}{4L}$ |
分析 应用库仑定律与场的叠加原理求出滑块在a点受到的电场力大小.研究aO段和ab段,由动能定理列式求aO两点间的电势差和摩擦力的大小.
解答 解:A、根据题意,不能确定滑块最终停在什么位置,故A错误.
B、根据库仑定律和电场的叠加原理可得,滑块在a点受到的电场力大小 F=k$\frac{Qq}{(\frac{L}{2})^{2}}$-k$\frac{Qq}{(\frac{3}{2}L)^{2}}$=$\frac{32kQq}{9{L}^{2}}$.故B错误.
CD、滑块从a到O的过程,由动能定理得:
-f$•\frac{L}{2}$+qUaO=$\frac{1}{2}m(2{v}_{0})^{2}$-$\frac{1}{2}m{v}_{0}^{2}$
滑块从a到b的过程,由动能定理得:
-fL=0-$\frac{1}{2}m{v}_{0}^{2}$
联立解得 f=$\frac{m{v}_{0}^{2}}{2L}$,UaO=$\frac{7m{v}_{0}^{2}}{4q}$.故C正确,D错误.
故选:C
点评 本题考查了动能定理的应用,分析清楚电荷的运动过程,应用动能定理、库仑定律公式与场的叠加原理即可正确解题.

练习册系列答案
相关题目
12. 小球从离地某一高度处落下,从落下到着地小球运动的速度-时间图象如图所示,则由图象可知(g=10m/s2)( )
小球从离地某一高度处落下,从落下到着地小球运动的速度-时间图象如图所示,则由图象可知(g=10m/s2)( )
 小球从离地某一高度处落下,从落下到着地小球运动的速度-时间图象如图所示,则由图象可知(g=10m/s2)( )
小球从离地某一高度处落下,从落下到着地小球运动的速度-时间图象如图所示,则由图象可知(g=10m/s2)( )| A. | 小球下落的最大速度为5m/s | |
| B. | 小球做自由落体运动 | |
| C. | 小球下落一半髙度时的速度是2$\sqrt{2}$m/s | |
| D. | 小球是从1.25米高度处落下的 |
7.物理学家通过艰辛的实验和理论研究探究自然规律,为人类的科学做出了巨大贡献,值得我们敬仰.下列描述中符合物理学史实的是( )
| A. | 奥斯特根据通电螺线管的磁场和条形磁铁的磁场相似性,提出了分子电流假说 | |
| B. | 开普勒发现了行星运动三定律,进而提出了万有引力定律 | |
| C. | 平均速度、瞬时速度和加速度等描述运动所需要的概念是伽利略首先建立的 | |
| D. | 法拉第发现了电磁感应现象并总结出了判断感应电流方向的规律 |


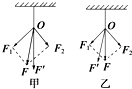 在“探究求合力的方法”实验中,
在“探究求合力的方法”实验中, 如图所示为正弦式交电流的电压u随时间t变化的图象,由图可知,该交变电流的电压的有效值为36V,频率为50Hz.
如图所示为正弦式交电流的电压u随时间t变化的图象,由图可知,该交变电流的电压的有效值为36V,频率为50Hz.