题目内容
12. 如图所示,一轻质弹簧两端各连一质量为m的滑块A和B,两滑块都置于光滑的水平面上.今有质量为$\frac{m}{4}$的子弹以水平速度v0射入A中不再穿出,试分析弹簧在什么状态下滑块B具有最大动能,其值是多少?
如图所示,一轻质弹簧两端各连一质量为m的滑块A和B,两滑块都置于光滑的水平面上.今有质量为$\frac{m}{4}$的子弹以水平速度v0射入A中不再穿出,试分析弹簧在什么状态下滑块B具有最大动能,其值是多少?
分析 对滑块A和子弹组成的系统研究,根据动量守恒求出共同的速度,当弹簧再次恢复原长时,B的动能最大,结合动量守恒和能量守恒求出动能的最大值.
解答 解:规定向右为正方向,子弹与A碰撞时,因碰撞时间极短,且A用弹簧与B相连,故可认为此时刻B未参与此过程,则子弹与A组成的系统动量守恒.设碰撞子弹与A的共同速度为vA,则有($\frac{m}{4}$)v0=(m+$\frac{m}{4}$)vA
代入数据解得vA=$\frac{{v}_{0}}{5}$.
此后,弹簧被压缩,B被加速,显然当弹簧再次恢复原长时,弹簧的弹性势能为零,B有最大速度vBm,即有最大动能EkBm.在此过程并以速度vA运动的滑块A与静止滑块B发生弹性碰撞,
根据动量守恒有:$(m+\frac{m}{4}){v}_{A}=(m+\frac{m}{4}){v}_{1}+m{v}_{Bm}$,
根据能量守恒得,$\frac{1}{2}(m+\frac{m}{4}){{v}_{A}}^{2}=\frac{1}{2}(m+\frac{m}{4}){{v}_{1}}^{2}$+$\frac{1}{2}m{{v}_{Bm}}^{2}$
解得:vBm=$\frac{2(m+\frac{m}{4})}{m+m+\frac{m}{4}}•\frac{{v}_{0}}{5}=\frac{2}{9}{v}_{0}$,
则最大动能EkBm=$\frac{1}{2}$m($\frac{2}{9}$v0)2=$\frac{2}{81}$mv${\;}_{0}^{2}$.
答:当弹簧再次恢复原长时B的动能最大,最大动能为$\frac{2}{81}$mv${\;}_{0}^{2}$.
点评 本题考查动量守恒定律及机械能守恒定律的应用,要注意能正确分析运动过程,明确能量转化的方向.

 如图所示,被一轻质弹簧系住的小球套在光滑的竖直杆上,弹簧的另一端固定在竖直墙面上并处于压缩状态,静止时弹簧水平,在小球被释放并运动到最低点的过程中,下列说法正确的是( )
如图所示,被一轻质弹簧系住的小球套在光滑的竖直杆上,弹簧的另一端固定在竖直墙面上并处于压缩状态,静止时弹簧水平,在小球被释放并运动到最低点的过程中,下列说法正确的是( )| A. | 弹簧的弹力一直做负功 | |
| B. | 小球的机械能先增大后减小 | |
| C. | 当弹簧处于原长时,重力的功率最大 | |
| D. | 小球的重力势能和弹簧的弹性势能之和先减少后增加 |
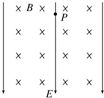 如图所示,空间存在相互垂直的匀强电场和匀强磁场,电场的方向竖直向下,磁场方向水平(图中垂直纸面向里),一带电油滴P恰好处于静止状态,则下列说法正确的是( )
如图所示,空间存在相互垂直的匀强电场和匀强磁场,电场的方向竖直向下,磁场方向水平(图中垂直纸面向里),一带电油滴P恰好处于静止状态,则下列说法正确的是( )| A. | 若仅撤去电场,P可能做匀加速直线运动 | |
| B. | 若仅撤去磁场,P一定做匀速直线运动 | |
| C. | 若给P一初速度,P不可能做匀速直线运动 | |
| D. | 若给P一初速度,P可能做匀速圆周运动 |
| A. | $\sqrt{2}$:1 | B. | $\sqrt{3}$:1 | C. | 1:$\sqrt{2}$ | D. | 1:1 |
 如图所示,把一块不带电的锌板接在验电器上,用紫外线灯照射锌板,验电器金属箔张开.下列说法正确的是( )
如图所示,把一块不带电的锌板接在验电器上,用紫外线灯照射锌板,验电器金属箔张开.下列说法正确的是( )| A. | 紫外线是不连续的 | |
| B. | 验电器金属箔带正电 | |
| C. | 从锌板逸出电子的动能都相等 | |
| D. | 改用红外灯照射,验电器金属箔一定张开 |
 如图所示,光滑水平面右端B处连接一个竖直的半径为R的半圆形轨道,在与B距离为x的A点,用水平恒力F将质量为m的小球从静止开始推到B处后撤去该恒力,小球沿半圆轨道运动到C处后又正好落回A点,求:
如图所示,光滑水平面右端B处连接一个竖直的半径为R的半圆形轨道,在与B距离为x的A点,用水平恒力F将质量为m的小球从静止开始推到B处后撤去该恒力,小球沿半圆轨道运动到C处后又正好落回A点,求:
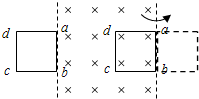 如图所示,空间存在竖直向下的有界匀强磁场B,一单匝边长为L,质量为m的正方形线框abcd放在水平桌面上,在水平外力作用下从左边界以速度v匀速进入磁场,当cd边刚好进入磁场后立刻撤去外力,线框ab边恰好能到达磁场的右边界,然后将线框以ab边为轴,以角速度ω匀速翻转到图示虚线位置.已知线框与桌面间动摩擦因数为μ,磁场宽度大于L,线框电阻为R,重力加速度为g,求:
如图所示,空间存在竖直向下的有界匀强磁场B,一单匝边长为L,质量为m的正方形线框abcd放在水平桌面上,在水平外力作用下从左边界以速度v匀速进入磁场,当cd边刚好进入磁场后立刻撤去外力,线框ab边恰好能到达磁场的右边界,然后将线框以ab边为轴,以角速度ω匀速翻转到图示虚线位置.已知线框与桌面间动摩擦因数为μ,磁场宽度大于L,线框电阻为R,重力加速度为g,求: