题目内容
6.如图所示,(a)图表示光滑平台上,物体A以初速度v0=3m/s滑到上表面粗糙的水平小车上,车与水平面间的动摩擦因数不计,(b)图为物体A与小车B的v-t图象,由此可知( )
| A. | 小车上表面长度为3m | |
| B. | 物体A与小车B的质量之比为1:2 | |
| C. | A与小车B上表面的动摩擦因数为0.2 | |
| D. | 整个过程A、B系统损失了$\frac{1}{3}$的能量 |
分析 由图示图象求出小车的长度.
由动量守恒定律可以求出质量之比.
由图示图象求出A的加速度,然后应用牛顿第二定律求出动摩擦因数.
应用能量守恒定律可以求出系统损失的能量.
解答 解:由速度图象可知,物体A在小车的上表面先做初速度为v0的匀减速运动,小车从静止开始做匀加速运动,2s后,物体和小车具有相同的速度v1=1m/s,随后物体和小车相对静止一起沿光滑的水平面做匀速运动.
A、图中的三角形的面积在数值上等于A和B的相对位移△S,小车的上表面的长度至少要比这个相对位移要大,所以小车的最小长度为:L=$\frac{1}{2}$×3×2=3m,小车上表面长度大于等于3m,故A错误;
B、由于水平面光滑,物体A和小车B组成的系统动量守恒,以A的初速度方向为正方向,由动量守恒定律得:mAv0=(mA+mB)v1,解得:$\frac{{m}_{A}}{{m}_{B}}$=$\frac{{v}_{1}}{{v}_{0}-{v}_{1}}$=$\frac{1}{3-1}$=$\frac{1}{2}$,故B正确;
C、由图示图象可知,A的加速度大小:a=$\frac{△v}{△t}$=$\frac{3-1}{2}$=1m/s2,由牛顿第二定律得:μmAg=mAa,解得:μ=0.1,故C错误;
D、由能量守恒定律可知,损失的能量:△E=$\frac{1}{2}$mAv02-$\frac{1}{2}$(mA+mB)v12=$\frac{2}{3}$•$\frac{1}{2}$mAv02,整个过程A、B系统损失了$\frac{2}{3}$的能量,故D错误;
故选:B.
点评 本题主要考查了动量守恒定律、能量守恒定律的直接应用,要求同学们能根据图象得出有效信息,难度适中.

练习册系列答案
相关题目
17. 如图所示,固定于水平面内的直角形光滑杆,OM与ON段均足够长,转角处为光滑的小圆弧.质量均为m的A、B两个有孔小球串在杆上,且被长为L的轻绳相连.忽略两球的大小,初态时,它们的位置如图中虚线所示,两球均静止,绳处于伸直状态,且与OM平行.现对B球施加沿ON方向的恒定拉力F,当B球运动$\frac{3}{5}$L,两球位置如图中实线所示,此时B球的速度大小为( )
如图所示,固定于水平面内的直角形光滑杆,OM与ON段均足够长,转角处为光滑的小圆弧.质量均为m的A、B两个有孔小球串在杆上,且被长为L的轻绳相连.忽略两球的大小,初态时,它们的位置如图中虚线所示,两球均静止,绳处于伸直状态,且与OM平行.现对B球施加沿ON方向的恒定拉力F,当B球运动$\frac{3}{5}$L,两球位置如图中实线所示,此时B球的速度大小为( )
 如图所示,固定于水平面内的直角形光滑杆,OM与ON段均足够长,转角处为光滑的小圆弧.质量均为m的A、B两个有孔小球串在杆上,且被长为L的轻绳相连.忽略两球的大小,初态时,它们的位置如图中虚线所示,两球均静止,绳处于伸直状态,且与OM平行.现对B球施加沿ON方向的恒定拉力F,当B球运动$\frac{3}{5}$L,两球位置如图中实线所示,此时B球的速度大小为( )
如图所示,固定于水平面内的直角形光滑杆,OM与ON段均足够长,转角处为光滑的小圆弧.质量均为m的A、B两个有孔小球串在杆上,且被长为L的轻绳相连.忽略两球的大小,初态时,它们的位置如图中虚线所示,两球均静止,绳处于伸直状态,且与OM平行.现对B球施加沿ON方向的恒定拉力F,当B球运动$\frac{3}{5}$L,两球位置如图中实线所示,此时B球的速度大小为( )| A. | $\sqrt{\frac{32FL}{25m}}$ | B. | $\sqrt{\frac{96FL}{25m}}$ | C. | $\sqrt{\frac{96FL}{125m}}$ | D. | $\sqrt{\frac{32FL}{125m}}$ |
15.一组铅蓄电池的电动势为48V,内阻不为零,以下说法中错误的是( )
| A. | 电路中每通过0.1C电量,铅蓄电池能把4.8J的化学能转变为电能 | |
| B. | 体积大的铅蓄电池比体积小的铅蓄电池的电动势大 | |
| C. | 电路中每通过0.1C电量,铅蓄电池内部非静电力做功为4.8J | |
| D. | 该铅蓄电池把其他形式能转化为电能的本领比一节干电池(电动势为1.5V)的强 |
16. 一根通有电流I的直铜棒用软导线挂在如图所示匀强磁场中,此时悬线中的张力大于零而小于铜棒的重力.欲使悬线中张力为零,可采用的方法有( )
一根通有电流I的直铜棒用软导线挂在如图所示匀强磁场中,此时悬线中的张力大于零而小于铜棒的重力.欲使悬线中张力为零,可采用的方法有( )
 一根通有电流I的直铜棒用软导线挂在如图所示匀强磁场中,此时悬线中的张力大于零而小于铜棒的重力.欲使悬线中张力为零,可采用的方法有( )
一根通有电流I的直铜棒用软导线挂在如图所示匀强磁场中,此时悬线中的张力大于零而小于铜棒的重力.欲使悬线中张力为零,可采用的方法有( )| A. | 适当增大电流,方向不变 | B. | 适当减小电流,并使它反向 | ||
| C. | 电流大小、方向不变,适当增强磁场 | D. | 使原电流反向,并适当减弱磁场 |
 时速可以达到360km/h的高铁,以其快捷、舒适的特色,越来越受到人们的青睐.你可曾想过这样一个物理问题:列车对水平轨道的压力和其运动方向之间是否相关.
时速可以达到360km/h的高铁,以其快捷、舒适的特色,越来越受到人们的青睐.你可曾想过这样一个物理问题:列车对水平轨道的压力和其运动方向之间是否相关. 在“验证机械能守恒定律”的实验中,已知电磁打点计时器所用的电源的频率为50Hz,查得当地的重力加速度g=9.80m/s2,测得所用的重物质量为1.00kg.实验中得到一条点迹清晰的纸带(如图所示),把第一个点记为O,另选连续的四个点A、B、C、D作为测量的点,经测量知道A、B、C、D各点到O点的距离分别为62.70cm、70.00cm、77.70cm、85.78cm.
在“验证机械能守恒定律”的实验中,已知电磁打点计时器所用的电源的频率为50Hz,查得当地的重力加速度g=9.80m/s2,测得所用的重物质量为1.00kg.实验中得到一条点迹清晰的纸带(如图所示),把第一个点记为O,另选连续的四个点A、B、C、D作为测量的点,经测量知道A、B、C、D各点到O点的距离分别为62.70cm、70.00cm、77.70cm、85.78cm.

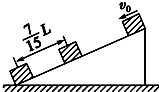 如图所示,小滑块在较长的斜面顶端,以初速度v0=2m/s、加速度a=2m/s2向下滑,在到达底端前1s内,所滑过的距离为斜面长度的$\frac{7}{15}$,求:小滑块在斜面上滑行的时间为多少?
如图所示,小滑块在较长的斜面顶端,以初速度v0=2m/s、加速度a=2m/s2向下滑,在到达底端前1s内,所滑过的距离为斜面长度的$\frac{7}{15}$,求:小滑块在斜面上滑行的时间为多少?