题目内容
4.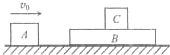 如图所示,木块C置于足够长的木板B上,A以v0=10m/s的初速度向右运动,与B碰撞后以4m/s的速率弹回.A、B、c的质量分别为mA=1kg,mB=4kg,mC=2kg.水平面光滑,B、C之间有摩擦.试求碰撞后C运动过程中的最大速度.
如图所示,木块C置于足够长的木板B上,A以v0=10m/s的初速度向右运动,与B碰撞后以4m/s的速率弹回.A、B、c的质量分别为mA=1kg,mB=4kg,mC=2kg.水平面光滑,B、C之间有摩擦.试求碰撞后C运动过程中的最大速度.
分析 A与B碰后的瞬间,B的速度最大,以A、B为系统,运用动量守恒定律求出B运动过程中的最大速率.
碰撞后C在B上滑行一段距离后与B保持相对静止,两者速度相同,此时C的速度最大,对BC系统研究,运用动量守恒定律求出共同速度的大小.
解答 解:A与B碰后瞬间,C的运动状态未变,B速度最大.
以A、B组成的系统为研究对象,碰撞过程系统动量守恒,以A的初速度方向为正方向,
由动量守恒定律得:mAv0+0=-mAvA+mBvB,
A、B碰撞后,B与C相互作用使B减速、C加速,由于B板足够长,
所以B和C能达到相同速度,二者共速后,C速度最大,
以B、C组成的系统为研究对象,以向右为正方向,
由动量守恒定律得:mBvB+0=(mB+mC)vC,
代入数据得:vC=$\frac{7}{3}$m/s,方向向右.
答:碰撞后C运动过程中的最大速度大小为$\frac{7}{3}$m/s,方向向右.
点评 本题考查了求木板、木块速度问题,分析清楚运动过程、正确选择研究对象与运动过程是解题的前提与关键,应用动量守恒定律即可正确解题;解题时要注意正方向的选择.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
15.如图所示,理想变压器的原、副线圈匝数之比为11:1,R=1Ω,原线圈允许通过电流的最大值为1A,副线圈ab两端电压随时间变化图象如图所示.则下列说法正确的是( )

| A. | 原线圈输入电压的有效值为242V | |
| B. | 原线圈两端交变电压的频率为550Hz | |
| C. | 副线圈中电流的最大值为11A | |
| D. | 为保证电路安全工作,滑动变阻器R′的阻值不得小于1Ω |
19.一个一价和一个二价的静止铜离子,经过同一电压加速后,再垂直射入同一匀强偏转电场,然后打在同一屏上,屏与偏转电场方向平行,下列说法正确的是( )
| A. | 二价铜离子打在屏上时的速度大 | |
| B. | 离子离开偏转电场后,二价铜离子飞到屏上用的时间短 | |
| C. | 离子经加速电场过程中,二价铜离子受电场力的功大 | |
| D. | 在离开偏转电场时,两种离子在电场方向上的位移不相等 |
14.宇航员在地球和某星球表面做了两个对比实验.实验一:在该星球和地球上以同样的高度和初速度平抛同一物体,发现其水平射程是地球上的4倍.实验二:飞船绕该星球表面的运行周期是它绕地球表面运行周期的2倍.则该星球与地球的质量之比和半径之比分别是( )
| A. | $\frac{1}{256}$,$\frac{1}{4}$ | B. | $\frac{1}{256}$,$\frac{1}{8}$ | C. | $\frac{1}{64}$,$\frac{1}{4}$ | D. | $\frac{1}{16}$,$\frac{1}{1}$ |

 如图所示,在水平固定的筒形绝热气缸中,用绝热的活塞封闭一部分气体,活塞与气缸之间无摩擦且不漏气.活塞的横截面积为0.2m2,外界大气压强为105Pa,气体温度为27℃时,活塞与汽缸底相距45cm.用一个电阻丝R给气体加热,活塞将会缓慢移动,使气缸内温度升高到77℃.
如图所示,在水平固定的筒形绝热气缸中,用绝热的活塞封闭一部分气体,活塞与气缸之间无摩擦且不漏气.活塞的横截面积为0.2m2,外界大气压强为105Pa,气体温度为27℃时,活塞与汽缸底相距45cm.用一个电阻丝R给气体加热,活塞将会缓慢移动,使气缸内温度升高到77℃. 带有等量异号电荷、相距10cm的平行板A和B之间有一个匀强电场(如图),电场强度E=4×104V/m,方向向下.电场中C点距B板3cm,D点距A板2cm.
带有等量异号电荷、相距10cm的平行板A和B之间有一个匀强电场(如图),电场强度E=4×104V/m,方向向下.电场中C点距B板3cm,D点距A板2cm.