题目内容
9.有质量分别为M1、M2的A、B两颗人造卫星,已知M1>M2,如果A和B在同一轨道上运动,则它们的线速度大小之比为1:1.如果A的轨道半径是B的轨道半径的2倍,则它们的线速度大小之比为$\sqrt{2}:2$.分析 根据万有引力提供圆周运动向心力,由卫星轨道半径关系求得线速度的大小关系.
解答 解:卫星圆周运动的向心力由万有引力提供,据此有:
$G\frac{mM}{{r}^{2}}=m\frac{{v}^{2}}{r}$
所以可得线速度$v=\sqrt{\frac{GM}{r}}$,即线速度大小与轨道半径平方根成反比,所以AB在同一条轨道上运动,线速度大小相等,有:vA:vB=1:1;
如果A的轨道半径是B轨道半径的2倍时,线速度大小之比为:
$\frac{{v}_{A}}{{v}_{B}}=\frac{\sqrt{\frac{GM}{{r}_{A}}}}{\sqrt{\frac{GM}{{r}_{B}}}}=\sqrt{\frac{{r}_{B}}{{r}_{A}}}$=$\frac{\sqrt{2}}{2}$
故答案为:1:1,$\sqrt{2}:2$
点评 本题关键是抓住万有引力提供圆周运动向心力,知道线速度的大小仅与半径和中心天体的质量有关,与环绕天体的质量大小无关.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
19.如图所示的电路,它表示的逻辑关系为( )


| A. | “与”门电路 | B. | “非”门电路 | C. | “或”门电路 | D. | 无法判定 |
18.有三个完全一样的金属球,A球带的电荷量为q,B、C均不带电.现要使B球带的电荷量为$\frac{3q}{8}$,应该怎么办?( )
| A. | A与B接触后分开 | |
| B. | A与B先接触,然后B与C接触后分开 | |
| C. | A与B先接触,然后B与C接触,最后B与A接触后分开 | |
| D. | A与C先接触,然后B与C接触,最后B与A接触后分开 |
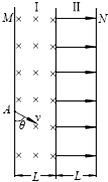 在真空室内,竖直放置的M、N板涂有荧光物质,如图所示.两板间竖直条形区域Ⅰ存在垂直纸面向里的匀强磁场,区域Ⅱ存在水平向右的匀强电场,磁场和电场均有界,宽度均为L,且足够长,磁场的强弱可以调节,电场强度恒为E.现有一束质子从A处连续不断地射入磁场,入射方向与M板成θ=60°夹角且与纸面平行,已知该质子束由两种速度的质子组成,一种速度大小为v的低速质子,另一种速度大小为3v的高速质子.当Ⅰ区域的磁场较强时,M板出现两个亮斑,缓慢改变磁场强弱,直到两个亮斑相继消失,此时观察到N板有两个亮斑.已知质子质量为m,电量为e,不计质子重力和相互间作用力,求:
在真空室内,竖直放置的M、N板涂有荧光物质,如图所示.两板间竖直条形区域Ⅰ存在垂直纸面向里的匀强磁场,区域Ⅱ存在水平向右的匀强电场,磁场和电场均有界,宽度均为L,且足够长,磁场的强弱可以调节,电场强度恒为E.现有一束质子从A处连续不断地射入磁场,入射方向与M板成θ=60°夹角且与纸面平行,已知该质子束由两种速度的质子组成,一种速度大小为v的低速质子,另一种速度大小为3v的高速质子.当Ⅰ区域的磁场较强时,M板出现两个亮斑,缓慢改变磁场强弱,直到两个亮斑相继消失,此时观察到N板有两个亮斑.已知质子质量为m,电量为e,不计质子重力和相互间作用力,求: 中子内有一个电荷量为+$\frac{2}{3}$e的上夸克和两个电荷量为$-\frac{1}{3}$e下夸克,一简单模型是三个夸克都在半径为r的同一圆周上,如图1所示.图2给出的四幅图中,能正确表示出各夸克所受静电作用力的是( )
中子内有一个电荷量为+$\frac{2}{3}$e的上夸克和两个电荷量为$-\frac{1}{3}$e下夸克,一简单模型是三个夸克都在半径为r的同一圆周上,如图1所示.图2给出的四幅图中,能正确表示出各夸克所受静电作用力的是( )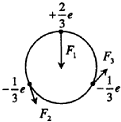



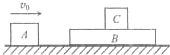 如图所示,木块C置于足够长的木板B上,A以v0=10m/s的初速度向右运动,与B碰撞后以4m/s的速率弹回.A、B、c的质量分别为mA=1kg,mB=4kg,mC=2kg.水平面光滑,B、C之间有摩擦.试求碰撞后C运动过程中的最大速度.
如图所示,木块C置于足够长的木板B上,A以v0=10m/s的初速度向右运动,与B碰撞后以4m/s的速率弹回.A、B、c的质量分别为mA=1kg,mB=4kg,mC=2kg.水平面光滑,B、C之间有摩擦.试求碰撞后C运动过程中的最大速度. 一新型赛车在水平专用测试道上进行测试,该车总质量为m=1×103kg,由静止开始沿水平测试道运动.传感设备记录其运动的速度-时间图象(v-t图象)如图所示.该车运动中受到的摩擦阻力(含空气阻力)恒定,且摩擦力与车队路面压力的比值为μ=0.2.赛车在0~5sd的v-t图线为直线,5s末起达到该车发动机的额定牵引功率并保持该功率行使,在5s~50s之间,赛车的v-t图线先是一段曲线,后为直线.g取10m/s2,求:
一新型赛车在水平专用测试道上进行测试,该车总质量为m=1×103kg,由静止开始沿水平测试道运动.传感设备记录其运动的速度-时间图象(v-t图象)如图所示.该车运动中受到的摩擦阻力(含空气阻力)恒定,且摩擦力与车队路面压力的比值为μ=0.2.赛车在0~5sd的v-t图线为直线,5s末起达到该车发动机的额定牵引功率并保持该功率行使,在5s~50s之间,赛车的v-t图线先是一段曲线,后为直线.g取10m/s2,求:
 检测一个标称值为5Ω的滑动变阻器.可供使用的器材如下:
检测一个标称值为5Ω的滑动变阻器.可供使用的器材如下: