题目内容
1. 2014年9月9日下午,合肥工业大学2014级学生消防演练活动在翡翠湖校区举行.演习中有个“模拟营救被困人员”的项目,某消防员作为伤员在被救楼层等待营救,一名选手在消防队员的指导下,背起伤员沿安全绳由静止开始往地面滑行,经过3s时间安全落地,为了获得演习中的一些数据,以提高训练质量,研究人员测出了下滑过程中轻绳受到的拉力与伤员和选手总重力的比值随时间变化的情况如图所示,取g=10m/s2,求:
2014年9月9日下午,合肥工业大学2014级学生消防演练活动在翡翠湖校区举行.演习中有个“模拟营救被困人员”的项目,某消防员作为伤员在被救楼层等待营救,一名选手在消防队员的指导下,背起伤员沿安全绳由静止开始往地面滑行,经过3s时间安全落地,为了获得演习中的一些数据,以提高训练质量,研究人员测出了下滑过程中轻绳受到的拉力与伤员和选手总重力的比值随时间变化的情况如图所示,取g=10m/s2,求:(1)伤员与选手下滑的最大速度的大小.
(2)伤员被救楼层距离地面的高度.
分析 (1)根据图象知人先加速后匀速再减速,通过牛顿第二定律求出0-1s加速度,根据v=at求速度为最大速度;
(2)分别求出各段的加速度,根据速度关系,利用运动学公式求的速度和位移;
解答 解:(1)由图可知在t=1s时,速度最大,由牛顿第二运动定律得mg-F1=ma1
其中在0~1s内F1=0.6mg,
解得:a1=4m/s2
最大速度vm=a1t1=4×1=4m/s
(2)在第0~1s内选手与伤员运动距离x1=$\frac{1}{2}$a${\;}_{1}{t}_{1}^{2}$=$\frac{1}{2}×4×{1}^{2}$=2m
在1~2s内选手与伤员受力平衡,做匀速直线运动x2=vmt2=4×1=4m
在2~3s内由牛顿第二运动定律可得F2-mg=ma2
解得选手与伤员减速下滑的加速度大小为a2=2m/s2
在这段时间内下滑的末速度为vt=vm-a2t3=2m/s
减速下滑距离为x3=$\frac{{v}_{m}+{v}_{1}}{2}{t}_{3}$=$\frac{4+2}{2}×1$=3m
伤员被救楼层距离地面的高度为:x=x1+x2+x3=9m
答:(1)伤员与选手下滑的最大速度的大小为4m/s.
(2)伤员被救楼层距离地面的高度为9m.
点评 本题主要考查了牛顿第二定律和运动学公式的熟练程度,抓住每段的运动即可;

练习册系列答案
相关题目
12.质量相等的甲、乙两颗卫星分别贴近某星球表面和地球表面围绕其做匀速圆周运动,已知该星球和地球的密度相同,半径之比为2:1,则( )
| A. | 甲、乙两颗卫星的加速度之比等于2;1 | |
| B. | 甲、乙两颗卫星所受的向心力之比等于1:1 | |
| C. | 甲、乙两颗卫星的线速度之比等于1:2 | |
| D. | 甲、乙两颗卫星的周期之比等于1:1 |
16. 如图所示,美洲狮是一种凶猛的食肉猛兽,也是噬杀成性的“杂食家”在跳跃方面有着惊人的“天赋”,它“厉害的一跃”水平距离可达44英尺,高达11英尺,设美洲狮做“厉害的一跃”离开地面时的速度方向与水平面的夹角为α,若不计空气阻力,美洲狮可看做质点,则tanα等于( )
如图所示,美洲狮是一种凶猛的食肉猛兽,也是噬杀成性的“杂食家”在跳跃方面有着惊人的“天赋”,它“厉害的一跃”水平距离可达44英尺,高达11英尺,设美洲狮做“厉害的一跃”离开地面时的速度方向与水平面的夹角为α,若不计空气阻力,美洲狮可看做质点,则tanα等于( )
 如图所示,美洲狮是一种凶猛的食肉猛兽,也是噬杀成性的“杂食家”在跳跃方面有着惊人的“天赋”,它“厉害的一跃”水平距离可达44英尺,高达11英尺,设美洲狮做“厉害的一跃”离开地面时的速度方向与水平面的夹角为α,若不计空气阻力,美洲狮可看做质点,则tanα等于( )
如图所示,美洲狮是一种凶猛的食肉猛兽,也是噬杀成性的“杂食家”在跳跃方面有着惊人的“天赋”,它“厉害的一跃”水平距离可达44英尺,高达11英尺,设美洲狮做“厉害的一跃”离开地面时的速度方向与水平面的夹角为α,若不计空气阻力,美洲狮可看做质点,则tanα等于( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
6. 如图所示,物体A和B的重力分别为8N和3N,不计弹簧秤、细线的重力和一切摩擦,弹簧的劲度系数K=100N/m,在弹性范围内,弹簧的伸长量为( )
如图所示,物体A和B的重力分别为8N和3N,不计弹簧秤、细线的重力和一切摩擦,弹簧的劲度系数K=100N/m,在弹性范围内,弹簧的伸长量为( )
 如图所示,物体A和B的重力分别为8N和3N,不计弹簧秤、细线的重力和一切摩擦,弹簧的劲度系数K=100N/m,在弹性范围内,弹簧的伸长量为( )
如图所示,物体A和B的重力分别为8N和3N,不计弹簧秤、细线的重力和一切摩擦,弹簧的劲度系数K=100N/m,在弹性范围内,弹簧的伸长量为( )| A. | 8cm | B. | 3cm | C. | 5cm | D. | 11cm |
13.图甲中理想变压器原、副线圈的匝数之比为n1:n2=5:1,电阻R=20Ω,L1、L2为规格相同的两只小灯泡,S1为单刀双掷开关.原线圈接正弦交变电源,输入电压u随时间t的变化关系如图乙所示.现将S1接1、S2闭合,此时L2正常发光的功率为P,下列说法正确的是( )


| A. | 输入电压u的表达式u=20$\sqrt{2}$sin50πtV | |
| B. | 只断开S2后,L1、L2的功率均小于$\frac{P}{4}$ | |
| C. | 只断开S2后,原线圈的输入功率大于$\frac{P}{2}$ | |
| D. | 若S1换接到2后,R消耗的电功率为0.8W |
10. 如图所示,一束光从空气射到直角三棱柱ABC的侧面AB上,进入三棱镜后从另一侧面AC射出,调整入射光的方向,当光线第一次射到AC恰不穿过时,测出入射光与AB面的夹角θ为30°,求此三棱镜的折射率.
如图所示,一束光从空气射到直角三棱柱ABC的侧面AB上,进入三棱镜后从另一侧面AC射出,调整入射光的方向,当光线第一次射到AC恰不穿过时,测出入射光与AB面的夹角θ为30°,求此三棱镜的折射率.
 如图所示,一束光从空气射到直角三棱柱ABC的侧面AB上,进入三棱镜后从另一侧面AC射出,调整入射光的方向,当光线第一次射到AC恰不穿过时,测出入射光与AB面的夹角θ为30°,求此三棱镜的折射率.
如图所示,一束光从空气射到直角三棱柱ABC的侧面AB上,进入三棱镜后从另一侧面AC射出,调整入射光的方向,当光线第一次射到AC恰不穿过时,测出入射光与AB面的夹角θ为30°,求此三棱镜的折射率.
11.一理想变压器原、副线圈的匝数比为44:1,原线圈输入电压的变化规律如图甲所示,副线圈所接电路如图乙所示,P为滑动变阻器的触头.下列说法正确的是( )
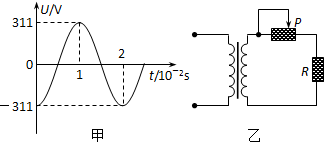

| A. | 副线圈输出电压的频率为100Hz | |
| B. | 副线圈输出电压的有效值为5V | |
| C. | P向左移动时,变压器原、副线圈的电流都减小 | |
| D. | P向左移动时,变压器的输入功率增加 |

 现有一根长为L=1m的刚性轻绳(绷紧瞬间绳长度不变),其一端固定于O点,另一端系着质量为m=0.5kg的小球(可视为质点),将小球提至O点正上方的A点处,此时绳刚好伸直且无张力,如图所示,不计空气阻力,g取10m/s2,若现在将小球以速度v0=1m/s水平抛出的瞬间,则:
现有一根长为L=1m的刚性轻绳(绷紧瞬间绳长度不变),其一端固定于O点,另一端系着质量为m=0.5kg的小球(可视为质点),将小球提至O点正上方的A点处,此时绳刚好伸直且无张力,如图所示,不计空气阻力,g取10m/s2,若现在将小球以速度v0=1m/s水平抛出的瞬间,则: