题目内容
6.研究某星系内行星的运动,需要知道恒星的质量,已知其中某行星的半径为R,质量为m,恒星与该行星中心间距为r,行星表面的重力加速度为g,行星绕恒星公转的周期为T.则恒星的质量为( )| A. | $\frac{{4{π^2}{r^3}}}{{{T^2}{R^2}g}}$ | B. | $\frac{{{T^2}{R^2}g}}{{4{π^2}m{r^3}}}$ | C. | $\frac{{4{π^2}mg}}{{{T^2}r}}$ | D. | $\frac{{4{π^2}m{r^3}}}{{{T^2}{R^2}g}}$ |
分析 根据万有引力等于重力得出万有引力常量,通过行星绕恒星运动,结合万有引力提供向心力求出恒星的质量.
解答 解:根据万有引力等于重力得,$G\frac{mm′}{{R}^{2}}=m′g$,解得G=$\frac{g{R}^{2}}{m}$.
行星绕恒星运动,根据万有引力提供向心力有:$G\frac{Mm}{{r}^{2}}=mr\frac{{4π}^{2}}{{T}^{2}}$,
联立解得M=$\frac{4{π}^{2}m{r}^{3}}{{T}^{2}{R}^{2}g}$.
故选:D.
点评 解决本题的关键掌握万有引力定律的两个重要理论:1、万有引力等于重力,2、万有引力提供向心力,并能灵活运用.

练习册系列答案
相关题目
17.一个标有“220V,60W”的电灯泡,当工作电压为110V,它的实际功率( )
| A. | 等于15W | B. | 大于15W | C. | 小于15W | D. | 无法确定 |
14.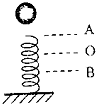 如图所示,自由下落的小球下落一段时间后,与轻质弹簧接触,从它接触弹簧开始,到弹簧压缩到最短的过程中,即弹簧上端位置由A→O→B,且弹簧被压缩到O位置时小球所受弹力等于重力,则小球速度最大时,弹簧上端位于( )
如图所示,自由下落的小球下落一段时间后,与轻质弹簧接触,从它接触弹簧开始,到弹簧压缩到最短的过程中,即弹簧上端位置由A→O→B,且弹簧被压缩到O位置时小球所受弹力等于重力,则小球速度最大时,弹簧上端位于( )
 如图所示,自由下落的小球下落一段时间后,与轻质弹簧接触,从它接触弹簧开始,到弹簧压缩到最短的过程中,即弹簧上端位置由A→O→B,且弹簧被压缩到O位置时小球所受弹力等于重力,则小球速度最大时,弹簧上端位于( )
如图所示,自由下落的小球下落一段时间后,与轻质弹簧接触,从它接触弹簧开始,到弹簧压缩到最短的过程中,即弹簧上端位置由A→O→B,且弹簧被压缩到O位置时小球所受弹力等于重力,则小球速度最大时,弹簧上端位于( )| A. | A位置 | B. | B位置 | C. | OB之间某一位置 | D. | O位置 |
1. 如图所示,三块相同的小木块从相同的高度由静止开始同时释放,其中A做自由落体运动,B在自由下落的中途被一水平方向的子弹射入,C在释放的瞬间被一水平方向的子弹射入.则关于它们的下落时间tA、tB、tC的关系,正确的是( )
如图所示,三块相同的小木块从相同的高度由静止开始同时释放,其中A做自由落体运动,B在自由下落的中途被一水平方向的子弹射入,C在释放的瞬间被一水平方向的子弹射入.则关于它们的下落时间tA、tB、tC的关系,正确的是( )
 如图所示,三块相同的小木块从相同的高度由静止开始同时释放,其中A做自由落体运动,B在自由下落的中途被一水平方向的子弹射入,C在释放的瞬间被一水平方向的子弹射入.则关于它们的下落时间tA、tB、tC的关系,正确的是( )
如图所示,三块相同的小木块从相同的高度由静止开始同时释放,其中A做自由落体运动,B在自由下落的中途被一水平方向的子弹射入,C在释放的瞬间被一水平方向的子弹射入.则关于它们的下落时间tA、tB、tC的关系,正确的是( )| A. | tA=tB=tC | B. | tA=tB<tC | C. | tA<tB<tC | D. | tA=tC<tB |
15.一物体做匀变速直线运动,某时刻速度的大小为4m/s,1s后速度大小变为10m/s,在这1s内的该物体的( )
| A. | 物体一定向同一个方向运动 | B. | 物体的运动方向可能发生改变 | ||
| C. | 加速度的大小可能小于4m/s2 | D. | 加速度的大小可能大于10m/s2 |
 如图所示,在xoy平面y>O的区域内有沿y轴负方向的匀强电场,在y<O的区域内有垂直于xoy平面向里的匀强磁场.一质量为m、电荷量为q的带电粒子从坐标为(2l,l)的P点以初速度v0沿x轴负方向开始运动,恰能从坐标原点O进入磁场,不计带电粒子所受的重力.
如图所示,在xoy平面y>O的区域内有沿y轴负方向的匀强电场,在y<O的区域内有垂直于xoy平面向里的匀强磁场.一质量为m、电荷量为q的带电粒子从坐标为(2l,l)的P点以初速度v0沿x轴负方向开始运动,恰能从坐标原点O进入磁场,不计带电粒子所受的重力.
 在研究两个共点力合成的实验中得到如图所示的合力F与两个分力的夹角θ的关系图象.求两个分力的大小分别为多少?这两个力的合力的变化范围为多少?
在研究两个共点力合成的实验中得到如图所示的合力F与两个分力的夹角θ的关系图象.求两个分力的大小分别为多少?这两个力的合力的变化范围为多少?