题目内容
9. 如图,质量m为5kg的物块(看作质点)在外力F1和F2的作用下正沿某一水平面向右做匀速直线运动.已知F1大小为50N,方向斜向右上方,与水平面夹角a=37°,F2大小为30N,方向水平向左,物块的速度v0大小为11m/s.当物体运动到距初始位置距离x0=5m时,撤掉F1,(重力加速度为g=10m/s2,sin37°=0.6,cos37°=0.8)求:
如图,质量m为5kg的物块(看作质点)在外力F1和F2的作用下正沿某一水平面向右做匀速直线运动.已知F1大小为50N,方向斜向右上方,与水平面夹角a=37°,F2大小为30N,方向水平向左,物块的速度v0大小为11m/s.当物体运动到距初始位置距离x0=5m时,撤掉F1,(重力加速度为g=10m/s2,sin37°=0.6,cos37°=0.8)求:(1)物块与水平地面之间的动摩擦因数μ.
(2)求撤掉F1以后,物块在6S末距初始位置的距离.
分析 (1)物块做匀速运动,根据共点力的平衡条件和摩擦力的计算公式求解动摩擦因数;
(2)根据牛顿运动定律求解撤掉F1后减速运动的加速度和减速运动时间、位移;再求出向左加速运动的位移,然后求解物块在6S末距初始位置的距离.
解答 解:(1)物块做匀速运动,根据共点力的平衡条件可得:f+F2=F1cosα,
摩擦力为:f=μ(mg-F1sinα),
联立得:μ=0.5;
(2)撤掉F1后减速运动的加速度为:${a}_{1}=\frac{{F}_{2}+μmg}{m}=\frac{30+25}{5}m/{s}^{2}=11m/{s}^{2}$
设经过t1向右运动速度变为0,有:${t}_{1}=\frac{{v}_{0}}{{a}_{1}}=\frac{11}{11}s=1s$,
此时向右位移,有:${x}_{1}=\frac{{v}_{0}}{2}{t}_{1}=\frac{11}{2}×1=5.5m$
后5s物块向左运动的加速度为:${a}_{2}=\frac{{F}_{2}-μmg}{m}=\frac{30-25}{5}=1m/{s}^{2}$
后5s向左位移为:${x}_{2}=\frac{1}{2}{a}_{2}{t}_{2}^{2}=\frac{1}{2}×1×{5}^{2}=12.5m$
物块在6S末距初始位置的距离为:△x=x2-(x0+x1)12.5-(5+5.5)=2m.
答:(1)物块与水平地面之间的动摩擦因数为0.5.
(2)求撤掉F1以后,物块在6S末距初始位置的距离为2m.
点评 对于牛顿第二定律的综合应用问题,关键是弄清楚物体的运动过程和受力情况,利用牛顿第二定律或运动学的计算公式求解加速度,再根据题目要求进行解答;知道加速度是联系静力学和运动学的桥梁.

 习题精选系列答案
习题精选系列答案 如图所示,小球C置于光滑的半球形凹槽B内,B放在长木板A上.整个装置处于静止状态.在缓慢减小长木板的倾角θ的过程中,下列说法正确的是( )
如图所示,小球C置于光滑的半球形凹槽B内,B放在长木板A上.整个装置处于静止状态.在缓慢减小长木板的倾角θ的过程中,下列说法正确的是( )| A. | C对B的压力渐减小 | B. | C对B的压力逐渐增大 | ||
| C. | C对B的压力大小不变 | D. | C对B的压力方向不断改变 |
 如图所示,两根水平放置的相互平行的金属导轨ab、cd,表面光滑,处在竖直向上的匀强磁场中,金属棒PQ垂直于导轨放在上面,以速度v向右匀速运动,欲使棒PQ停下来,下面的措施可行的是(导轨足够长,棒PQ有电阻)( )
如图所示,两根水平放置的相互平行的金属导轨ab、cd,表面光滑,处在竖直向上的匀强磁场中,金属棒PQ垂直于导轨放在上面,以速度v向右匀速运动,欲使棒PQ停下来,下面的措施可行的是(导轨足够长,棒PQ有电阻)( )| A. | 在PQ右侧垂直于导轨再放上一根同样的金属棒 | |
| B. | 在PQ右侧垂直于导轨再放上一根质量和电阻均比棒PQ大的金属棒 | |
| C. | 将导轨的a、c两端用导线连接起来 | |
| D. | 在导轨的a、c两端用导线连接一个电容器 |
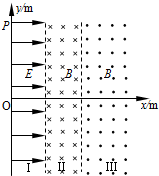 如图所示,空间被平行界面分为三个区域,Ⅰ区域存在匀强电场,电场强度E可取不同值,其左边界与y轴重合;Ⅱ区域磁场方向垂直纸面向里、Ⅲ区域磁场方向垂直纸面向外,磁感应强度均为B,Ⅰ、Ⅱ区域宽度均为d,Ⅲ区域右侧无限制;平面直角坐标系中点P(0,3d).质量m、电荷量+q粒子从坐标原点O由静止释放进入电场.粒子的重力不计.求:
如图所示,空间被平行界面分为三个区域,Ⅰ区域存在匀强电场,电场强度E可取不同值,其左边界与y轴重合;Ⅱ区域磁场方向垂直纸面向里、Ⅲ区域磁场方向垂直纸面向外,磁感应强度均为B,Ⅰ、Ⅱ区域宽度均为d,Ⅲ区域右侧无限制;平面直角坐标系中点P(0,3d).质量m、电荷量+q粒子从坐标原点O由静止释放进入电场.粒子的重力不计.求:
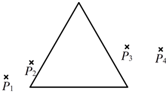 某同学测量一块玻璃三棱镜的折射率,经正确操作,插下了四枚大头针P1、P2和P3、P4,如图所示.
某同学测量一块玻璃三棱镜的折射率,经正确操作,插下了四枚大头针P1、P2和P3、P4,如图所示. 如图所示,两平行金属板A、B长L=8cm,两板间距离d=8cm,A板比B板电势高300V,一不计重力的带正电的粒子电荷量q=10-10C,质量m=10-20kg,沿电场中心线RD垂直电场线飞入电场,初速度υ0=2×106m/s,粒子飞出平行板电场后可进入界面MN、PS间的无电场区域.已知两界面MN、PS相距为12cm,D是中心线RD与界面PS的交点.求:
如图所示,两平行金属板A、B长L=8cm,两板间距离d=8cm,A板比B板电势高300V,一不计重力的带正电的粒子电荷量q=10-10C,质量m=10-20kg,沿电场中心线RD垂直电场线飞入电场,初速度υ0=2×106m/s,粒子飞出平行板电场后可进入界面MN、PS间的无电场区域.已知两界面MN、PS相距为12cm,D是中心线RD与界面PS的交点.求: 如图所示,空间区域Ⅰ、Ⅱ有匀强电场和匀强磁场,其中电场方向竖直向上,区域Ⅰ中磁场垂直纸面向内,区域Ⅱ中磁场垂直纸面向外,磁感应强度大小均为B=$\frac{mv}{qd}$,矩形区域足够长,宽为2d,在AD边中点O处有一粒子源,沿纸面向磁场中各方向均匀地辐射出速率均为v的带电粒子,该粒子进入场区后恰能作匀速圆周运动,带电粒子质量m,电荷量为q.已知重力加速度为g.
如图所示,空间区域Ⅰ、Ⅱ有匀强电场和匀强磁场,其中电场方向竖直向上,区域Ⅰ中磁场垂直纸面向内,区域Ⅱ中磁场垂直纸面向外,磁感应强度大小均为B=$\frac{mv}{qd}$,矩形区域足够长,宽为2d,在AD边中点O处有一粒子源,沿纸面向磁场中各方向均匀地辐射出速率均为v的带电粒子,该粒子进入场区后恰能作匀速圆周运动,带电粒子质量m,电荷量为q.已知重力加速度为g.