��Ŀ����
17�� ��ͼ��ʾ������a��b��c�����糡�����������棬���ڵ�����֮��ĵ��Ʋ���ȣ���Uab=Ubc��ʵ��Ϊһ��������ʵ���ڵ糡��������ͨ��������ʱ���˶��켣��P��Q�������켣�ϵ����㣬�ݴ˿�֪��������
��ͼ��ʾ������a��b��c�����糡�����������棬���ڵ�����֮��ĵ��Ʋ���ȣ���Uab=Ubc��ʵ��Ϊһ��������ʵ���ڵ糡��������ͨ��������ʱ���˶��켣��P��Q�������켣�ϵ����㣬�ݴ˿�֪��������| A�� | �����������У�a�ĵ������ | |
| B�� | �����ʵ���P����еĵ����ܱ���Q����еĵ�����С | |
| C�� | �����ʵ�ͨ��P��ʱ�Ķ��ܱ�ͨ��Q��ʱ�� | |
| D�� | �����ʵ�ͨ��P��ʱ�ļ��ٶȱ�ͨ��Q��ʱ�� |
���� �糡��������洹ֱ���糡���ܵĵط��糡��ǿ�ȴ糡����ĵط��糡��ǿ��С���ص糡�ߵķ����ƽ��ͣ��糡���������������ܼ�С���糡�������������������ӣ������Щ֪ʶ������
���  �⣺A���ɹ켣������������糡��Ӧָ�����߰��࣬��������洹ֱ���糡�ߴ�ֱ�ô������棩����������ɵ����������볡ǿ����һ�£��ʿɻ����糡�߷�����ͼ��ʾ��˳�ŵ糡�߷�����ƽ��ͣ���֪a�ĵ�����ߣ���A��ȷ��
�⣺A���ɹ켣������������糡��Ӧָ�����߰��࣬��������洹ֱ���糡�ߴ�ֱ�ô������棩����������ɵ����������볡ǿ����һ�£��ʿɻ����糡�߷�����ͼ��ʾ��˳�ŵ糡�߷�����ƽ��ͣ���֪a�ĵ�����ߣ���A��ȷ��
BC������ʵ���P�˶���Q���糡���������ٶȷ���ļн�С��90�㣬�������������ܼ�С����������֮�������Q��P���ٶȻ�λ�������ķ���нǴ���90���������������������ܼ�С�����ʵ���P����еĵ����ܱ���Q����еĵ����ܴ�ͨ��P��ʱ�Ķ��ܱ�ͨ��Q��ʱС����B��C����
D��P���������Q���ܣ��������ܴ���ǿ�����P���ܵĵ糡�����ٶȾʹ�D��ȷ��
��ѡ��AD��
���� ��ǿ����֪ʶ��ѧϰ������ס�糡�ߺ͵�������ص㣬���ɽ�����⣮

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
4������˵����ȷ���ǣ�������
| A�� | ¬ɪ��ͨ������������ɢ��ʵ���������������Ӻ����� | |
| B�� | ��������n=4����̬����ԭ������ܼ�ԾǨʱ�����ɲ���6�ֲ�ͬƵ�ʵĹ��� | |
| C�� | ������Ԫ�صİ�˥����ԭ�������Ļ�ѧ״̬���ⲿ�����й� | |
| D�� | �����ºͦ��������ߣ������ߵĴ�������ǿ |
8�� ��ͼ��ʾ����ǿ�糡����һ����ABCD������AB=2cm��BC=1cm��CD=4cm��A��B��C������Ʒֱ�Ϊ��A=12V����B=6V����C=3V��������˵����ȷ���ǣ�������
��ͼ��ʾ����ǿ�糡����һ����ABCD������AB=2cm��BC=1cm��CD=4cm��A��B��C������Ʒֱ�Ϊ��A=12V����B=6V����C=3V��������˵����ȷ���ǣ�������
 ��ͼ��ʾ����ǿ�糡����һ����ABCD������AB=2cm��BC=1cm��CD=4cm��A��B��C������Ʒֱ�Ϊ��A=12V����B=6V����C=3V��������˵����ȷ���ǣ�������
��ͼ��ʾ����ǿ�糡����һ����ABCD������AB=2cm��BC=1cm��CD=4cm��A��B��C������Ʒֱ�Ϊ��A=12V����B=6V����C=3V��������˵����ȷ���ǣ�������| A�� | ��һ���Ӵ�A���ƶ���D�㣬�����˷��糡������3eV | |
| B�� | ��һ���Ӵ�A���ƶ���D�㣬�糡������5eV | |
| C�� | ��ǿ�糡��ǿ����СֵΪ3��102V/m | |
| D�� | ��ǿ�糡��ǿ����СֵΪ2��102V/m |
5��ijЩ�����������ľ������ϣ���Ϊ̫������������Ϊ���������ǡ�������������ߡ���ơ�CX�����ǡ��������ǡ��ľ��ǣ�������̫���и����������ǡ������������ӳ����ǵ����������衰CX�����ڵ�����ƽ���ڵ�Բ�ܹ�������У����з����������ת����һ�£�����뾶Ϊ����ͬ�����ǹ���뾶��$\frac{1}{5}$��������
| A�� | ��CX�����ٶ��ǵ���ͬ�������ٶȵ�$\sqrt{5}$�� | |
| B�� | ��CX���ļ��ٶ��ǵ���ͬ�����Ǽ��ٶȵ�5�� | |
| C�� | ��CX������ڵ������ϵĹ۲��������˶� | |
| D�� | ��CX��Ҫʵ�ֶԸ�����ϡ��������ǡ������ȱ���ֱ�Ӽ��� |
2������ѡ�������ж���ȷ���ǣ�������
| A�� | ������ʱ���ŵأ�����������Ħ������������˵�Ħ����������ǰ�Ķ��� | |
| B�� | ��������Ӿʱ������ˮ�е��˶��Ƕ�ˮ��ǰ������ˮ���˵�������������� | |
| C�� | ���������ϵ����壬�������������ж����ε�ѹ�������������֧�������֣���ѹ���Ȳ�����֧��������� | |
| D�� | �������뷴��������Ӧ�����������������з����������������ȱ仯����������Ҳ��������Ӧ�仯 |
6�� ��ͼ��ʾ������A��B������Ϊm������ͨ��һ����ϵ��Ϊk���ᵯ����������ʼʱB���ڵ����ϣ�A��B�����ھ�ֹ״̬��������ͨ��ϸ�������ؽ�A������������ΪL1ʱ��B��Ҫ�뿪���棬�˹���������ΪW1������A������������A�����ľ���ΪL2ʱ��B��Ҫ�뿪���棬��ʱA���ٶ�Ϊv���˹���������ΪW2������һֱ���ڵ������ڣ�������
��ͼ��ʾ������A��B������Ϊm������ͨ��һ����ϵ��Ϊk���ᵯ����������ʼʱB���ڵ����ϣ�A��B�����ھ�ֹ״̬��������ͨ��ϸ�������ؽ�A������������ΪL1ʱ��B��Ҫ�뿪���棬�˹���������ΪW1������A������������A�����ľ���ΪL2ʱ��B��Ҫ�뿪���棬��ʱA���ٶ�Ϊv���˹���������ΪW2������һֱ���ڵ������ڣ�������
 ��ͼ��ʾ������A��B������Ϊm������ͨ��һ����ϵ��Ϊk���ᵯ����������ʼʱB���ڵ����ϣ�A��B�����ھ�ֹ״̬��������ͨ��ϸ�������ؽ�A������������ΪL1ʱ��B��Ҫ�뿪���棬�˹���������ΪW1������A������������A�����ľ���ΪL2ʱ��B��Ҫ�뿪���棬��ʱA���ٶ�Ϊv���˹���������ΪW2������һֱ���ڵ������ڣ�������
��ͼ��ʾ������A��B������Ϊm������ͨ��һ����ϵ��Ϊk���ᵯ����������ʼʱB���ڵ����ϣ�A��B�����ھ�ֹ״̬��������ͨ��ϸ�������ؽ�A������������ΪL1ʱ��B��Ҫ�뿪���棬�˹���������ΪW1������A������������A�����ľ���ΪL2ʱ��B��Ҫ�뿪���棬��ʱA���ٶ�Ϊv���˹���������ΪW2������һֱ���ڵ������ڣ�������| A�� | L1=L2=$\frac{mg}{k}$ | B�� | W2��W1 | C�� | W1=mgL1 | D�� | W2=mgL2+$\frac{m{v}^{2}}{2}$ |
7��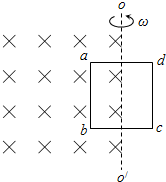 ��ͼ��ʾ�����Ѿ��αպϵ��߿�abcdһ�봦�ڴŸ�Ӧǿ��ΪB��ˮƽ�н���ǿ�ų��У��߿����ΪS������ΪR���߿��������������غϵ���ֱ�̶�ת��OO���Խ��ٶȦ�����ת�����̶�ת��ǡ��λ����ǿ�ų����ұ߽磮���߿��и�Ӧ��������ЧֵΪ��������
��ͼ��ʾ�����Ѿ��αպϵ��߿�abcdһ�봦�ڴŸ�Ӧǿ��ΪB��ˮƽ�н���ǿ�ų��У��߿����ΪS������ΪR���߿��������������غϵ���ֱ�̶�ת��OO���Խ��ٶȦ�����ת�����̶�ת��ǡ��λ����ǿ�ų����ұ߽磮���߿��и�Ӧ��������ЧֵΪ��������
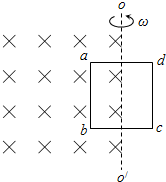 ��ͼ��ʾ�����Ѿ��αպϵ��߿�abcdһ�봦�ڴŸ�Ӧǿ��ΪB��ˮƽ�н���ǿ�ų��У��߿����ΪS������ΪR���߿��������������غϵ���ֱ�̶�ת��OO���Խ��ٶȦ�����ת�����̶�ת��ǡ��λ����ǿ�ų����ұ߽磮���߿��и�Ӧ��������ЧֵΪ��������
��ͼ��ʾ�����Ѿ��αպϵ��߿�abcdһ�봦�ڴŸ�Ӧǿ��ΪB��ˮƽ�н���ǿ�ų��У��߿����ΪS������ΪR���߿��������������غϵ���ֱ�̶�ת��OO���Խ��ٶȦ�����ת�����̶�ת��ǡ��λ����ǿ�ų����ұ߽磮���߿��и�Ӧ��������ЧֵΪ��������| A�� | $\frac{{\sqrt{2}Bs��}}{4R}$ | B�� | $\frac{{\sqrt{2}Bs��}}{2R}$ | C�� | $\frac{Bs��}{4R}$ | D�� | $\frac{Bs��}{2R}$ |
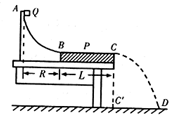 ����С���Q��ƽ��P֮��Ķ�Ħ��������ʵ��װ����ͼ��ʾ��AB�ǰ뾶�㹻��ĽϹ⻬�ķ�֮һԲ���������ˮƽ�̶����õ�P����ϱ���BC��B�����У�C����ˮƽ����Ĵ�ֱͶӰΪC�䣮�������ٶȴ�СΪg��ʵ�鲽�����£�
����С���Q��ƽ��P֮��Ķ�Ħ��������ʵ��װ����ͼ��ʾ��AB�ǰ뾶�㹻��ĽϹ⻬�ķ�֮һԲ���������ˮƽ�̶����õ�P����ϱ���BC��B�����У�C����ˮƽ����Ĵ�ֱͶӰΪC�䣮�������ٶȴ�СΪg��ʵ�鲽�����£� ��ͼ��ʾ��һ�����ΪԲ�ε��������壬�����һ��������ƽ����ֱ��AB�ķ����M�����벣���壬���������ǡ��ͨ��B�㣬�����ڲ������д������ٶ�Ϊ$\frac{{\sqrt{3}c}}{3}$��cΪ���٣�����
��ͼ��ʾ��һ�����ΪԲ�ε��������壬�����һ��������ƽ����ֱ��AB�ķ����M�����벣���壬���������ǡ��ͨ��B�㣬�����ڲ������д������ٶ�Ϊ$\frac{{\sqrt{3}c}}{3}$��cΪ���٣�����