题目内容
7.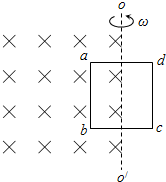 如图所示,单匝矩形闭合导线框abcd一半处于磁感应强度为B的水平有界匀强磁场中,线框面积为S,电阻为R.线框绕与其中心线重合的竖直固定转轴OO′以角速度ω匀速转动,固定转轴恰好位于匀强磁场的右边界.则线框中感应电流的有效值为( )
如图所示,单匝矩形闭合导线框abcd一半处于磁感应强度为B的水平有界匀强磁场中,线框面积为S,电阻为R.线框绕与其中心线重合的竖直固定转轴OO′以角速度ω匀速转动,固定转轴恰好位于匀强磁场的右边界.则线框中感应电流的有效值为( )| A. | $\frac{{\sqrt{2}Bsω}}{4R}$ | B. | $\frac{{\sqrt{2}Bsω}}{2R}$ | C. | $\frac{Bsω}{4R}$ | D. | $\frac{Bsω}{2R}$ |
分析 感应电动势最大值Em=BSω,由欧姆定律求出电流的最大值,由有效值的定义求出电流的有效值
解答 解:线圈中产生感应电动势最大值:Em=$\frac{1}{2}$BSω,
设感应电动势有效值为E,则:$\frac{{E}^{2}}{R}$T=$\frac{(\frac{BSω}{2\sqrt{2}})^{2}}{R}×T$,
电流I=$\frac{E}{R}$;
联立解得:I=$\frac{{\sqrt{2}Bsω}}{4R}$
故选:A.
点评 本题要注意因为只有一关线圈在磁场中,故求解最大值时,不能用总面积,只能用处在磁场中的面积来求.

练习册系列答案
相关题目
17. 如图所示,虚线a、b、c代表电场中三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )
如图所示,虚线a、b、c代表电场中三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )
 如图所示,虚线a、b、c代表电场中三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )
如图所示,虚线a、b、c代表电场中三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )| A. | 三个等势面中,a的电势最高 | |
| B. | 带电质点在P点具有的电势能比在Q点具有的电势能小 | |
| C. | 带电质点通过P点时的动能比通过Q点时大 | |
| D. | 带电质点通过P点时的加速度比通过Q点时大 |
12.下列说法正确的是( )
| A. | ${\;}_{6}^{14}$C经一次α衰变后成为${\;}_{7}^{14}$N | |
| B. | 氢原子的核外电子从半径较小的轨道跃迁到半径较大的轨道时,原子的能量增大 | |
| C. | 温度升高能改变放射性元素的半衰期 | |
| D. | 核反应方程应遵循质子数和中子数守恒 |
19.木星是绕太阳公转的行星之一,而木星的周围又有卫星绕木星公转.如果要通过观测求得木星的质量M,已知万有引力常量为G,则需要测量的量及木星质量的计算式是( )
| A. | 卫星的公转周期T1和轨道半径r1,$M=\frac{4{π}^{2}{r}_{1}^{3}}{G{T}_{1}^{2}}$ | |
| B. | 卫星的公转周期T1和轨道半径r1,$M=\frac{G{T}_{1}^{2}}{4{π}^{2}{r}_{1}^{3}}$ | |
| C. | 木星的公转周期T2和轨道半径r2,$M=\frac{4{π}^{2}{r}_{2}^{3}}{G{T}_{2}^{2}}$ | |
| D. | 木星的公转周期T2和轨道半径r2,$M=\frac{G{T}_{2}^{2}}{4{π}^{2}{r}_{2}^{3}}$ |
17. 如图所示,相距为d的两条水平虚线L1、L2之间是方向水平向里的匀强磁场,磁感应强度为B,质量为m、电阻为R的正方形线圈abcd边长为L(L<d),将线圈在磁场上方高h处由静止释放,cd边刚进入磁场时速度为v0,cd边刚离开磁场时速度也为v0,则线圈穿越磁场的过程中(从cd边刚入磁场一直到ab边刚离开磁场)( )
如图所示,相距为d的两条水平虚线L1、L2之间是方向水平向里的匀强磁场,磁感应强度为B,质量为m、电阻为R的正方形线圈abcd边长为L(L<d),将线圈在磁场上方高h处由静止释放,cd边刚进入磁场时速度为v0,cd边刚离开磁场时速度也为v0,则线圈穿越磁场的过程中(从cd边刚入磁场一直到ab边刚离开磁场)( )
 如图所示,相距为d的两条水平虚线L1、L2之间是方向水平向里的匀强磁场,磁感应强度为B,质量为m、电阻为R的正方形线圈abcd边长为L(L<d),将线圈在磁场上方高h处由静止释放,cd边刚进入磁场时速度为v0,cd边刚离开磁场时速度也为v0,则线圈穿越磁场的过程中(从cd边刚入磁场一直到ab边刚离开磁场)( )
如图所示,相距为d的两条水平虚线L1、L2之间是方向水平向里的匀强磁场,磁感应强度为B,质量为m、电阻为R的正方形线圈abcd边长为L(L<d),将线圈在磁场上方高h处由静止释放,cd边刚进入磁场时速度为v0,cd边刚离开磁场时速度也为v0,则线圈穿越磁场的过程中(从cd边刚入磁场一直到ab边刚离开磁场)( )| A. | 感应电流做功为mgL | |
| B. | 感应电流做功为2mgd | |
| C. | 线圈的最小速度不可能为$\frac{mgR}{{{B^2}{L^2}}}$ | |
| D. | 线圈的最小速度一定为$\sqrt{2g(h+L-d)}$ |
 如图所示:矩形线框ABCD由n=50匝组成,BC边长l1=0.4m,AB边长l2=0.2m,整个线圈的电阻R=2Ω,在B=0.1T的匀强磁场中以AD边为轴转动,转动角速度ω=50rad/s,求:
如图所示:矩形线框ABCD由n=50匝组成,BC边长l1=0.4m,AB边长l2=0.2m,整个线圈的电阻R=2Ω,在B=0.1T的匀强磁场中以AD边为轴转动,转动角速度ω=50rad/s,求: 滑板运动受到青少年的追棒,如图是某滑板运动员在一次表演时的一部分赛道在竖直平面内的示意图.DB段为光滑的四分之一圆弧,AB段水平且粗糙恰与圆弧DB在B点相切,赛道固定在水平面上.一个质量为m的运动员(可视为质点)从赛道的A端以初动能E冲上水平赛道AB,并沿着赛道运动,然后由DB弧滑下后停在赛道AB段的中点.已知AB长为L,重力加速度为g,求:
滑板运动受到青少年的追棒,如图是某滑板运动员在一次表演时的一部分赛道在竖直平面内的示意图.DB段为光滑的四分之一圆弧,AB段水平且粗糙恰与圆弧DB在B点相切,赛道固定在水平面上.一个质量为m的运动员(可视为质点)从赛道的A端以初动能E冲上水平赛道AB,并沿着赛道运动,然后由DB弧滑下后停在赛道AB段的中点.已知AB长为L,重力加速度为g,求:
 图甲为某同学“验证力的平行四边形定则”的装置图,A为固定橡皮筋的图钉,O为橡皮条与细绳的结点,OB和OC为细绳.实验时,需要两次拉伸橡皮条;一次是通过两细绳用两个弹簧秤互成角度地拉橡皮条;另一次是用一个弹簧秤通过细绳拉橡皮条.图乙是在白纸上根据实验结果画出的图.
图甲为某同学“验证力的平行四边形定则”的装置图,A为固定橡皮筋的图钉,O为橡皮条与细绳的结点,OB和OC为细绳.实验时,需要两次拉伸橡皮条;一次是通过两细绳用两个弹簧秤互成角度地拉橡皮条;另一次是用一个弹簧秤通过细绳拉橡皮条.图乙是在白纸上根据实验结果画出的图.