题目内容
9．
如图所示，某一运动员从弧形雪坡上沿水平方向飞出后，又落回到斜面雪坡上，若斜面雪坡的倾角为θ，飞出时的速度大小为v0，不计空气阻力，运动员飞出后在空中的姿势保持不变，重力加速度为g，则（ ）| A． | 如果v0不同，则该运动员落到雪坡时的速度方向也就不同 | |
| B． | 不论v0多大，该运动员落到雪坡时的速度方向都是相同的 | |
| C． | 运动员在空中经历的时间是$\frac{2{v}_{0}tanθ}{g}$ | |
| D． | 运动员落到雪坡时的速度大小是$\frac{{v}_{0}}{cosθ}$ |
分析 运动员做平抛运动，水平方向做匀速直线运动，竖直方向做自由落体运动，由斜面倾角的正切等于竖直位移与水平位移之比，从而求出运动的时间；因此可求出竖直方向的运动速度，求解运动员落地点时的速度大小；同时可求出竖起高度与抛出点和落地点的距离
解答 解：设在空中飞行时间为t，运动员在竖直方向做自由落体运动，水平方向做匀速直线运动；
C、运动员竖直位移与水平位移之比：$\frac{y}{x}$=$\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}$=$\frac{gt}{2{v}_{0}}$=tanθ，则有飞行的时间t=$\frac{2{v}_{0}tanθ}{g}$，故C正确；
D、竖直方向的速度大小为：vy=gt=2v0tanθ，运动员落回雪坡时的速度大小为：v=$\sqrt{{v}_{0}^{2}{+v}_{y}^{2}}$=v0$\sqrt{1+4（tanθ）^{2}}$，故D错误；
AB、设运动员落到雪坡时的速度方向与水平方向夹角为α，则tanα=$\frac{{v}_{y}}{{v}_{x}}=\frac{2{v}_{0}tanθ}{{v}_{0}}$=2tanθ，由此可知，运动员落到雪坡时的速度方向与初速度方向无关，初速度不同，运动员落到雪坡时的速度方向相同，故A错误，B正确；
故选：BC．
点评 解决本题的关键知道平抛运动在水平方向做匀速直线运动，在竖直方向做自由落体运动，并结合运动学规律来解题．注意不能将速度与水平面的夹角看成位移与水平面的夹角．
练习册系列答案
相关题目
19．用如图1所示的实验装置来验证牛顿第二定律．
①为消除摩擦力的影响，实验前平衡摩擦力的具体操作为：取下沙桶，把木板不带滑轮的一端适当垫高并反复调节，直到轻推小车后，小车能沿木板做匀速直线运动．
②在实验过程，某次打出纸带如图2，相邻计数点A、B、C、D、E之间还有4个点未画出，该纸带对应的加速度为：0.60 m/s2 （保留两位有效数字）；
③某次实验测得的数据如下表所示．根据这些数据在图3坐标图中描点并作出a-$\frac{1}{m}$图线．从a-$\frac{1}{m}$图线求得合外力大小为0.30N（保留两位有效数字）．
①为消除摩擦力的影响，实验前平衡摩擦力的具体操作为：取下沙桶，把木板不带滑轮的一端适当垫高并反复调节，直到轻推小车后，小车能沿木板做匀速直线运动．
②在实验过程，某次打出纸带如图2，相邻计数点A、B、C、D、E之间还有4个点未画出，该纸带对应的加速度为：0.60 m/s2 （保留两位有效数字）；
③某次实验测得的数据如下表所示．根据这些数据在图3坐标图中描点并作出a-$\frac{1}{m}$图线．从a-$\frac{1}{m}$图线求得合外力大小为0.30N（保留两位有效数字）．
| $\frac{1}{m}$/kg-1 | a/m•s2 |
| 4.0 | 1.2 |
| 3.6 | 1.1 |
| 2.0 | 0.6 |
| 1.4 | 0.4 |
| 1.0 | 0.3 |
20．某同学用内阻约为几十欧的电流表，内阻约为几千欧的电压表等仪器，测定在不同工作状态下小灯泡的电阻．
（1）请在如图1的方框中画出测量电路的原理图；并根据所画原理图将以下实物图（图2）补充完整．
（2）在闭合开关前，实物图中滑动变阻器的滑动触头应在右端（填写“左”或“右”）．
（3）实验中该同学记录了7组数据，请在如图3的坐标纸中描绘出小灯泡的I-U图线．
（1）请在如图1的方框中画出测量电路的原理图；并根据所画原理图将以下实物图（图2）补充完整．
（2）在闭合开关前，实物图中滑动变阻器的滑动触头应在右端（填写“左”或“右”）．
（3）实验中该同学记录了7组数据，请在如图3的坐标纸中描绘出小灯泡的I-U图线．
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 电压/V | 0.00 | 0.40 | 0.80 | 1.20 | 1.60 | 2.00 | 2.40 |
| 电流/A | 0.00 | 0.02 | 0.05 | 0.12 | 0.20 | 0.31 | 0.44 |
4．某实验小组利用如题图甲所示的装置探究功和动能变化的关系，他们将宽度为d的挡光片固定在小车上，用不可伸长的细线将其通过一个定滑轮与砝码盘相连，在水平桌面上的A、B两点各安装一个光电门，记录小车通过A、B时的遮光时间，小车中可以放置砝码．
（1）实验主要步骤如下：
①将木板略微倾斜以平衡摩擦力，使得细线拉力做的功等于合力对小车做的功．
②将小车停在C点，在砝码盘中放上砝码，小车在细线拉动下运动，记录此时小车、小车中砝码和挡光片的质量之和为M，砝码盘和盘中砝码的总质量为m，小车通过A、B时的遮光时间分别为t1、t2，则小车通过A、B过程中动能的变化量△E=$\frac{1}{2}M（\frac{d}{{t}_{2}^{\;}}）_{\;}^{2}-\frac{1}{2}M（\frac{d}{{t}_{1}^{\;}}）_{\;}^{2}$（用字母M、t1、t2、d表示）．
③在小车中增减砝码或在砝码盘中增减砝码，重复②的操作．
④用游标卡尺测量挡光片的宽度d
（2）下表是他们测得的多组数据，其中M是小车、小车中砝码和挡光片的质量之和，|v22-v12|是两个速度的平方差，可以据此计算出动能变化量△E，取绳上拉力F大小近似等于砝码盘及盘中砝码的总重力，W是F在A、B间所做的功．表格中△E3=0.498J，W3=0.505J（结果保留三位有效数字）．
（3）若在本实验中没有平衡摩擦力，假设小车与水平长木板之间的动摩擦因数为μ．利用上面的实验器材完成如下操作：保证小车质量不变，改变砝码盘中砝码的数量（取绳上拉力近似为砝码盘及盘中砝码的总重力），测得多组m、t1、t2的数据，并得到m与${（{\frac{1}{t_2}}）^2}-{（{\frac{1}{t_1}}）^2}$的关系图象，如图乙所示．已知图象在纵轴上的截距为b，直线PQ的斜率为k，A、B两点的距离为s，挡光片的宽度为d，则μ=$\frac{b{d}_{\;}^{2}}{2gsk}$（用字母b、d、s、k、g表示）．
（1）实验主要步骤如下：
①将木板略微倾斜以平衡摩擦力，使得细线拉力做的功等于合力对小车做的功．
②将小车停在C点，在砝码盘中放上砝码，小车在细线拉动下运动，记录此时小车、小车中砝码和挡光片的质量之和为M，砝码盘和盘中砝码的总质量为m，小车通过A、B时的遮光时间分别为t1、t2，则小车通过A、B过程中动能的变化量△E=$\frac{1}{2}M（\frac{d}{{t}_{2}^{\;}}）_{\;}^{2}-\frac{1}{2}M（\frac{d}{{t}_{1}^{\;}}）_{\;}^{2}$（用字母M、t1、t2、d表示）．
③在小车中增减砝码或在砝码盘中增减砝码，重复②的操作．
④用游标卡尺测量挡光片的宽度d
（2）下表是他们测得的多组数据，其中M是小车、小车中砝码和挡光片的质量之和，|v22-v12|是两个速度的平方差，可以据此计算出动能变化量△E，取绳上拉力F大小近似等于砝码盘及盘中砝码的总重力，W是F在A、B间所做的功．表格中△E3=0.498J，W3=0.505J（结果保留三位有效数字）．
| 次数 | M/kg | |v22-v12|/（m/s）2 | △E/J | F/N | W/J |
| 1 | 1.000 | 0.380 | 0.190 | 0.400 | 0.200 |
| 2 | 1.000 | 0.826 | 0.413 | 0.840 | 0.420 |
| 3 | 1.000 | 0.996 | △E3 | 1.010 | W3 |
| 4 | 2.000 | 1.20 | 1.20 | 2.420 | 1.21 |
| 5 | 2.000 | 1.42 | 1.42 | 2.860 | 1.43 |
14．
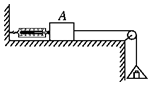如图所示，放在水平桌面上的木块A处于静止状态，所挂的砝码和托盘的总质量为0.6kg，弹簧测力计读数为2N，滑轮摩擦不计．若轻轻取走盘中的部分砝码，使砝码和托盘的总质量减少到0.3kg，则将会出现的情况是（g取10m/s2）（ ）
如图所示，放在水平桌面上的木块A处于静止状态，所挂的砝码和托盘的总质量为0.6kg，弹簧测力计读数为2N，滑轮摩擦不计．若轻轻取走盘中的部分砝码，使砝码和托盘的总质量减少到0.3kg，则将会出现的情况是（g取10m/s2）（ ）| A． | 弹簧测力计的读数将不变 | B． | A仍静止不动 | ||
| C． | A与桌面间的摩擦力不变 | D． | A所受的合力将要变大 |
1．给滑块一初速度10m/s使它沿光滑斜面向上做匀减速运动，加速度大小为5m/s2，当滑块速度大小为5m/s时，所用时间可能是（ ）
| A． | 1s | B． | 2s | C． | 2.5s | D． | 3s |
18．一辆汽车做匀速直线运动，速度为20m/s，关闭发动机后以大小为4m/s2的加速度做匀减速运动，则关闭发动机后前6s内的位移大小为（ ）
| A． | 48m | B． | 192m | C． | 50m | D． | 108m |
19．2016年10月19日凌晨，神舟十一号飞船与天宫二号目标飞行器在离地面393km的近圆轨道上成功进行了空间交会对接．对接轨道所处的空间存在极其稀薄的大气，下列说法正确的是（ ）
| A． | 为实现对接，两者运行速度的大小都应介于第一宇宙速度和第二宇宙速度之间 | |
| B． | 航天员在天宫二号中处于失重状态，说明航天员不受地球引力作用 | |
| C． | 如不干涉，天宫二号的轨道高度将缓慢增加 | |
| D． | 如不加干预，在运行一段时间后，天宫二号的动能会增加 |