题目内容
13.如图所示,x轴上有两个波源S1和S2,间距1.6m,两波源的振动图象分别为图甲和图乙.已知两波源产生的波的波长均为0.8m,质点O位于两波源连线的中点.求:
(1)两列波的传播速度的大小.
(2)写出O点的振动方程(t=0时,两列波都已传到O点).
(3)S1S2间各个振动减弱点的位置离S1的距离.
分析 (1)由图求出它们的周期,然后由波速与周期的关系即可求出波速.
(2)根据波的叠加原理研究O的振动是加强还是减弱,然后结合振幅、周期即可写出振动方程;
(3)根据波的叠加原理研究C的振动是加强还是减弱,根据时间与周期的关系分析t2=0.9s时刻A点的振动情况.
解答 解:(1)由图可知二者的周期都是1.0s,所以波速相等,都是:
v=$\frac{λ}{T}=\frac{0.8}{1}=0.8$m/s
(2)由质点O位于两波源连线的中点可知,O点到两个波源S1和S2的距离相等,又由图可知,两个波源起振的方向相同,所以O点为振动的加强点;
O点的振幅为二者振幅负和,则:A=A1+A2=2+3=5cm
O振动的圆频率:$ω=\frac{2π}{T}=\frac{2π}{1}=2π$rad/s
两个波源起振的方向都向上,所以O点起振的方向也向上,所以O点的振动方程为:y=5sin2πt(cm)
(3)波源起振的方向相同,则到两个波源的距离差为半波长的奇数倍的点为振动的减弱点,设两个波源的间距为L,与波源S1间距为x处的波程差:δ=r2-r1=x-(L-x)=2x-L
由于:$\frac{λ}{2}=0.4$m
所以,当δ=±0.4m时,${x}_{1}=1m\\;,{x}_{2}=0.6m$,x2=0.6m
当δ=±1.2m时,x3=1.4m,x4=0.2m
答:(1)两列波的传播速度的大小都是0.8m/s.
(2)O点的振动方程为y=5sin2πt(cm).
(3)S1S2间各个振动减弱点的位置离S1的距离分别为0.2m,0.6m,1.0m和1.4m.
点评 本题通过两个质点的振动图象,读出同一时刻两质点的状态,根据波形,得出两点间距离与波长的关系,是典型的多解问题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
3.如图所示,a、b两个可视为质点的小球分别在轴线竖直、内壁光滑的两圆锥的内侧面上以相同的角速度做匀速圆周运动.已知两圆锥面与水平面的夹角分别为45°和30°,则( )


| A. | 两球做匀速圆周运动的半径相等 | |
| B. | 两球做匀速圆周运动的线速度大小相等 | |
| C. | a球的向心加速度小于b球的向心加速度 | |
| D. | a球离地面的高度大于b球离地面的高度 |
4. 在观察布朗运动时,从微粒在A点开始计时,每隔30s记下微粒的一个位置,得到B、C、D、E、F、G等点,然后用直线依次连接,如图所示,则下列说法正确的是( )
在观察布朗运动时,从微粒在A点开始计时,每隔30s记下微粒的一个位置,得到B、C、D、E、F、G等点,然后用直线依次连接,如图所示,则下列说法正确的是( )
 在观察布朗运动时,从微粒在A点开始计时,每隔30s记下微粒的一个位置,得到B、C、D、E、F、G等点,然后用直线依次连接,如图所示,则下列说法正确的是( )
在观察布朗运动时,从微粒在A点开始计时,每隔30s记下微粒的一个位置,得到B、C、D、E、F、G等点,然后用直线依次连接,如图所示,则下列说法正确的是( )| A. | 图中记录的是分子无规则运动的情况 | |
| B. | 图中记录的是微粒做布朗运动的轨迹 | |
| C. | 微粒在前30s内的位移大小一定等于AB的长度 | |
| D. | 微粒在75s末时的位置一定在CD的连线上,但不可能在CD中点 |
1.关于分子间的作用力,下列说法中正确的是( )
| A. | 当两个分子间相互作用表现为引力时,分子间没有斥力 | |
| B. | 两个分子间距离减小,分子间的引力和斥力都增大 | |
| C. | 两个分子从相距很远处到逐渐靠近的过程中,分子间的相互作用力逐渐变大 | |
| D. | 将体积相同的水和酒精混在一起,发现总体积小于混合前水和酒精的体积之和,说明分子间存在引力 |
18. 如图所示,B、C、D、E、F五个球并排放置在光滑的水平面上,B、C、D、E四球质量相等,而F球质量小于B球质量,A球的质量等于F球质量,A球以速度v0向B球运动,所发生的碰撞均为弹性碰撞,则碰撞之后( )
如图所示,B、C、D、E、F五个球并排放置在光滑的水平面上,B、C、D、E四球质量相等,而F球质量小于B球质量,A球的质量等于F球质量,A球以速度v0向B球运动,所发生的碰撞均为弹性碰撞,则碰撞之后( )
 如图所示,B、C、D、E、F五个球并排放置在光滑的水平面上,B、C、D、E四球质量相等,而F球质量小于B球质量,A球的质量等于F球质量,A球以速度v0向B球运动,所发生的碰撞均为弹性碰撞,则碰撞之后( )
如图所示,B、C、D、E、F五个球并排放置在光滑的水平面上,B、C、D、E四球质量相等,而F球质量小于B球质量,A球的质量等于F球质量,A球以速度v0向B球运动,所发生的碰撞均为弹性碰撞,则碰撞之后( )| A. | 五个小球静止,一个小球运动 | B. | 四个小球静止,两个小球运动 | ||
| C. | 三个小球静止,三个小球运动 | D. | 六个小球都运动 |
2. 如图所示,在x轴上方存在垂直纸面向里的磁感应强度为B的匀强磁场,x轴下方存在垂直纸面向外的磁感应强度为$\frac{B}{2}$的匀强磁场.一带负电的粒子从原点O以与x轴成30°角斜向上射入磁场,且在x轴上方运动的半径为R.不计重力,则( )
如图所示,在x轴上方存在垂直纸面向里的磁感应强度为B的匀强磁场,x轴下方存在垂直纸面向外的磁感应强度为$\frac{B}{2}$的匀强磁场.一带负电的粒子从原点O以与x轴成30°角斜向上射入磁场,且在x轴上方运动的半径为R.不计重力,则( )
 如图所示,在x轴上方存在垂直纸面向里的磁感应强度为B的匀强磁场,x轴下方存在垂直纸面向外的磁感应强度为$\frac{B}{2}$的匀强磁场.一带负电的粒子从原点O以与x轴成30°角斜向上射入磁场,且在x轴上方运动的半径为R.不计重力,则( )
如图所示,在x轴上方存在垂直纸面向里的磁感应强度为B的匀强磁场,x轴下方存在垂直纸面向外的磁感应强度为$\frac{B}{2}$的匀强磁场.一带负电的粒子从原点O以与x轴成30°角斜向上射入磁场,且在x轴上方运动的半径为R.不计重力,则( )| A. | 粒子经偏转一定能回到原点O | |
| B. | 粒子在x轴上方和下方两磁场中运动的半径之比为1:2 | |
| C. | 粒子完成一次周期性运动的时间为$\frac{πm}{3qB}$ | |
| D. | 粒子第二次射入x轴上方磁场时,沿x轴前进3R |
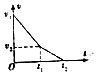
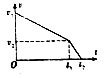
 如图所示,在山体下的水平地面上有一静止长木板,某次山体滑坡,有石块从山坡上滑下后,恰好以速度v1滑上长木板,石块与长木板、长木板与水平地面之间都存在摩擦,设最大静摩擦力大小等于滑动摩擦力的大小,且石块始终不滑出木板,下面给出了石块在长木板上滑行的v-t图象,其中正确的是( )
如图所示,在山体下的水平地面上有一静止长木板,某次山体滑坡,有石块从山坡上滑下后,恰好以速度v1滑上长木板,石块与长木板、长木板与水平地面之间都存在摩擦,设最大静摩擦力大小等于滑动摩擦力的大小,且石块始终不滑出木板,下面给出了石块在长木板上滑行的v-t图象,其中正确的是( )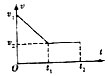


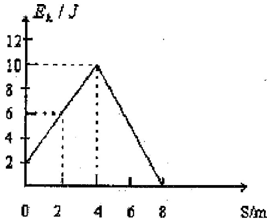 质量m=1kg的物体,在水平拉力F的作用下,沿粗糙水平面运动,经过位移4m时,拉力F停止作用,运动到位移是8m时物体停止.运动过程中物体动能随位移变化的Ek-s的图象如图所示.g取10m/s2.求:
质量m=1kg的物体,在水平拉力F的作用下,沿粗糙水平面运动,经过位移4m时,拉力F停止作用,运动到位移是8m时物体停止.运动过程中物体动能随位移变化的Ek-s的图象如图所示.g取10m/s2.求: