题目内容
17.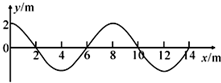 在均匀介质中,t=0时刻振源O沿+y方向开始振动,t=0.9时x轴上0至14m范围第一次出现图示的简谐横波波形,由此可以判断:波的周期为0.4s,x=20m处质点在0~1.2s内通过的路程为4m.
在均匀介质中,t=0时刻振源O沿+y方向开始振动,t=0.9时x轴上0至14m范围第一次出现图示的简谐横波波形,由此可以判断:波的周期为0.4s,x=20m处质点在0~1.2s内通过的路程为4m.
分析 机械波在传播过程中,介质中各个质点的起振方向都与波源的起振方向相同,可判断出图中波最前列的质点的振动方向,确定出已有波形的长度,写出时间与周期的关系,从而求得周期.根据距离求出波从图示时刻传到x=20m处的时间,分析该质点在0~1.2s内振动的时间,即可求解路程.
解答 解:振源O沿+y方向开始振动,介质中各个质点均沿+y方向开始振动,而图中x=14m处质点此刻正沿-y方向振动,则x轴上0至14m范围第一次出现图示的简谐横波波形,x=14m右侧还有半个波长的波形未画,所以从t=0时刻到t=0.9s时刻波传播的距离为:
x=18m=2$\frac{1}{4}$λ,
传播的时间为:△t=0.9s=2$\frac{1}{4}$T
得:T=0.4s.
波速为:v=$\frac{λ}{T}$=$\frac{8}{0.4}$m/s=20m/s
波从x=18m传到x=20m处的时间为:t=$\frac{x}{v}$=$\frac{20-18}{20}$s=0.1s
故x=20m处质点在0~1.2s内已经振动了时间为:t′=1.2s-0.9s-0.1s=0.2s=$\frac{1}{2}$T
质点在一个周期内通过的路程是4A,则在t′=$\frac{1}{2}$T内通过的路程是:S=2A=2×2m=4m.
故答案为:0.4,4
点评 本题关键抓住介质中任何质点的起振方向均与波源的起振方向相同,确定出已有波形的长度,不能简单地认为波在0.9s传播的距离为14m.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8. 如图1所示,小物体从竖直弹簧上方离地高h1处 由静止释放,其动能Ek与离地高度h的关系如图2所示.其中高度从h1下降到h2,图象为直线,其余部分为曲线,h3对应图象的最高点,轻弹簧劲度系数为k,弹簧的重力不计.小物体质量为m,重力加速度为g.以下说法正确的是( )
如图1所示,小物体从竖直弹簧上方离地高h1处 由静止释放,其动能Ek与离地高度h的关系如图2所示.其中高度从h1下降到h2,图象为直线,其余部分为曲线,h3对应图象的最高点,轻弹簧劲度系数为k,弹簧的重力不计.小物体质量为m,重力加速度为g.以下说法正确的是( )
 如图1所示,小物体从竖直弹簧上方离地高h1处 由静止释放,其动能Ek与离地高度h的关系如图2所示.其中高度从h1下降到h2,图象为直线,其余部分为曲线,h3对应图象的最高点,轻弹簧劲度系数为k,弹簧的重力不计.小物体质量为m,重力加速度为g.以下说法正确的是( )
如图1所示,小物体从竖直弹簧上方离地高h1处 由静止释放,其动能Ek与离地高度h的关系如图2所示.其中高度从h1下降到h2,图象为直线,其余部分为曲线,h3对应图象的最高点,轻弹簧劲度系数为k,弹簧的重力不计.小物体质量为m,重力加速度为g.以下说法正确的是( )| A. | 小物体下降至高度h2时,弹簧的弹性势能为0 | |
| B. | 小物体下落至高度h3时,弹簧的弹性势能最大 | |
| C. | 小物体下落至高度h3时,弹簧的弹性势能最小 | |
| D. | 小物体从高度h1下降到h5,弹簧的弹性势能为mg(h1-h5) |
5.一列简谐横波沿x轴传播,t=0时刻的波形如图甲所示,图乙为质点a的振动图象,则( )


| A. | 波向左传播,频率为5Hz | |
| B. | 波向右传播,波速为20m/s | |
| C. | 从该时刻起经过0.05s时,质点a和b的加速度相同 | |
| D. | 从该时刻起经过0.15s,a、b两点的位移都为2m |
9. 如图所示,长1m的轻质细杆,一端固定有一个质量为2kg的小球,另一端由电动机带动,使杆绕O点在竖直平面内做匀速圆周运动,小球的速率为2m/s.下列说法正确的是(g取10m/s2)( )
如图所示,长1m的轻质细杆,一端固定有一个质量为2kg的小球,另一端由电动机带动,使杆绕O点在竖直平面内做匀速圆周运动,小球的速率为2m/s.下列说法正确的是(g取10m/s2)( )
 如图所示,长1m的轻质细杆,一端固定有一个质量为2kg的小球,另一端由电动机带动,使杆绕O点在竖直平面内做匀速圆周运动,小球的速率为2m/s.下列说法正确的是(g取10m/s2)( )
如图所示,长1m的轻质细杆,一端固定有一个质量为2kg的小球,另一端由电动机带动,使杆绕O点在竖直平面内做匀速圆周运动,小球的速率为2m/s.下列说法正确的是(g取10m/s2)( )| A. | 小球通过最低点时,对杆的拉力大小是28N,处于超重状态 | |
| B. | 小球通过最高点时,对杆的拉力大小是28N,处于超重状态 | |
| C. | 小球通过最低点时,对杆的拉力大小是12N,处于失重状态 | |
| D. | 小球通过最高点时,对杆的压力大小是12N,处于失重状态 |
6. 如图所示,理想变压器原线圈两端接有交流电源,副线圈中三只灯泡都能正常发光,R为定值电阻.L为电感线圈.C为电容器.现保持原线圈两端输入电压的最大值不变,频率变为原来的一半.下列说法正确的是( )
如图所示,理想变压器原线圈两端接有交流电源,副线圈中三只灯泡都能正常发光,R为定值电阻.L为电感线圈.C为电容器.现保持原线圈两端输入电压的最大值不变,频率变为原来的一半.下列说法正确的是( )
 如图所示,理想变压器原线圈两端接有交流电源,副线圈中三只灯泡都能正常发光,R为定值电阻.L为电感线圈.C为电容器.现保持原线圈两端输入电压的最大值不变,频率变为原来的一半.下列说法正确的是( )
如图所示,理想变压器原线圈两端接有交流电源,副线圈中三只灯泡都能正常发光,R为定值电阻.L为电感线圈.C为电容器.现保持原线圈两端输入电压的最大值不变,频率变为原来的一半.下列说法正确的是( )| A. | 三只灯泡的亮度均不变 | B. | 副线圈两端的电压减小 | ||
| C. | 灯泡L1亮度不变,L2变暗,L3变亮 | D. | 灯泡L1亮度不变,L2变亮,L3变暗 |
7. 如图甲所示,质量m=2kg的物体以100J的初动能在粗糙的水平地面上滑行,其动能Ek随位移S变化的关系图象如图乙所示,则下列判断中正确的是( )
如图甲所示,质量m=2kg的物体以100J的初动能在粗糙的水平地面上滑行,其动能Ek随位移S变化的关系图象如图乙所示,则下列判断中正确的是( )
 如图甲所示,质量m=2kg的物体以100J的初动能在粗糙的水平地面上滑行,其动能Ek随位移S变化的关系图象如图乙所示,则下列判断中正确的是( )
如图甲所示,质量m=2kg的物体以100J的初动能在粗糙的水平地面上滑行,其动能Ek随位移S变化的关系图象如图乙所示,则下列判断中正确的是( )| A. | 物体运动的总位移大小为10m | B. | 物体运动的加速度大小为10m/s2 | ||
| C. | 物体运动的初速度大小为10m/s | D. | 物体所受的摩擦力大小为10N |

