题目内容
1.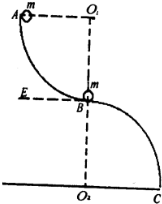 如图所示,有两个完全相同的半径为R的光滑$\frac{1}{4}$圆弧槽,在末端焊接成新的曲线槽ABC,并且固定在竖直面内,使得两个$\frac{1}{4}$圆弧槽所在的圆心O1、O2连线恰好过焊接点B,并垂直于水平地面O2C(且过B处的切线BE恰好为水平线),已知焊接处B也是光滑的,现有两个大小相等,质量均为m的非弹性小球,其中2静止在B点,让球1从曲线槽上端点A由静止开始自由下落,到B处与球2正碰后粘合一起沿槽下滑(已知重力加速度为g)
如图所示,有两个完全相同的半径为R的光滑$\frac{1}{4}$圆弧槽,在末端焊接成新的曲线槽ABC,并且固定在竖直面内,使得两个$\frac{1}{4}$圆弧槽所在的圆心O1、O2连线恰好过焊接点B,并垂直于水平地面O2C(且过B处的切线BE恰好为水平线),已知焊接处B也是光滑的,现有两个大小相等,质量均为m的非弹性小球,其中2静止在B点,让球1从曲线槽上端点A由静止开始自由下落,到B处与球2正碰后粘合一起沿槽下滑(已知重力加速度为g)(1)球在离水平地面O2C高度h为多大时离开轨道;
(2)球滑离轨道时速度v的大小是多少?
分析 对小球1由机械能守恒定律可求得碰前的速度,再由动量守恒定律求得碰后的速度;再对碰后到离开轨道过程进行分析,由机械能守恒定律及向心力公式可求得离开高度及速度.
解答 解:球1从A端滑到B处与2相碰之间,设速度为v,由机械能守恒定律可知:
mgR=$\frac{1}{2}$mv2
在B处2球相碰,碰后粘在一起,设向右为正方向,碰后速度为v′;
由动量守恒定律可得:
mv=2mv′
设小球在D处滑离轨道,脱离前的速度为v1,令∠BO2D=θ,由几何关系得脱离地面高度为h=Rcosθ;
由牛顿第二定律有:
2mgcosθ=2m$\frac{{v}_{1}^{2}}{R}$
从B滑到D处时,两球机械能守恒,则有:
2mgR(1-cosθ)+$\frac{1}{2}$•2mv′2=$\frac{1}{2}•2m$v12
联立解得:h=$\frac{5R}{6}$;v1=$\sqrt{\frac{5gR}{6}}$
答:(1)球在离水平地面O2C高度h为$\frac{5R}{6}$时离开轨道;
(2)球滑离轨道时速度v的大小是$\sqrt{\frac{5gR}{6}}$
点评 本题考查动量守恒、机械能守恒及向心力公式的应用,要注意正确分析物理过程,明确各过程中所对应的物理规律的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.通过归类和比较,有助于理解和掌握新概念、新知识.下列类比不正确的是( )
| A. | 点电荷可以与质点类比,都是理想化模型 | |
| B. | 机械波可以与电磁波类比,两者都可以在真空中传播 | |
| C. | 电场力做功可以与重力做功类比.两种力做功都与路径无关 | |
| D. | 电场线可以与磁感线类比,都是用假想的曲线形象化地描绘“场”的客观存在 |
16. 如图所示,足够长的光滑U型导轨宽度为L,其所在平面与水平面的夹角为α,上端连接一个阻值为R的电阻,置于磁感应强度大小为B,方向垂直于导轨平面向上的匀强磁场中,今有一质量为m、有效电阻r的金属杆沿框架由静止下滑,设磁场区域无限大,当金属杆下滑达到最大速度时,运动的位移为x,则( )
如图所示,足够长的光滑U型导轨宽度为L,其所在平面与水平面的夹角为α,上端连接一个阻值为R的电阻,置于磁感应强度大小为B,方向垂直于导轨平面向上的匀强磁场中,今有一质量为m、有效电阻r的金属杆沿框架由静止下滑,设磁场区域无限大,当金属杆下滑达到最大速度时,运动的位移为x,则( )
 如图所示,足够长的光滑U型导轨宽度为L,其所在平面与水平面的夹角为α,上端连接一个阻值为R的电阻,置于磁感应强度大小为B,方向垂直于导轨平面向上的匀强磁场中,今有一质量为m、有效电阻r的金属杆沿框架由静止下滑,设磁场区域无限大,当金属杆下滑达到最大速度时,运动的位移为x,则( )
如图所示,足够长的光滑U型导轨宽度为L,其所在平面与水平面的夹角为α,上端连接一个阻值为R的电阻,置于磁感应强度大小为B,方向垂直于导轨平面向上的匀强磁场中,今有一质量为m、有效电阻r的金属杆沿框架由静止下滑,设磁场区域无限大,当金属杆下滑达到最大速度时,运动的位移为x,则( )| A. | 在此过程中流过电阻R的电量为$\frac{Blx}{R+r}$ | |
| B. | 金属杆下滑的最大速度vm=$\frac{mgRsinα}{{B}^{2}{l}^{2}}$ | |
| C. | 在此过程中电阻R产生的焦耳热为mgxsinα-$\frac{1}{2}$mvm2 | |
| D. | 在此过程中导体棒克服安培力做功为$\frac{r}{R+r}$(mgxsinα-$\frac{1}{2}$mvm2) |
13.一颗子弹射穿透一块厚度为3.0cm的固定木板后速度减小到原来的$\frac{1}{2}$,假设子弹在穿过木板过程所受的阻力不变,则此后它还能射穿透同样材料木板的厚度最多为( )
| A. | 3.0cm | B. | 1.5cm | C. | 1.0cm | D. | 0.75cm |
8.若我国发射的某颗人造卫星,距离地球表面的高度恰等于地球的半径,设地球是均匀的球体,则下列描述正确的是( )
| A. | 该卫星的周期小于24 h | |
| B. | 该卫星可能绕着地轴上的任一点做圆周运动 | |
| C. | 该卫星的线速度可能大于7.9 km/s | |
| D. | 该卫星的角速度小于地球自转的角速度 |
 如图所示,在直角坐标系xOy平面内,第二象限中虚线MN平行于y轴,N点坐标为(-L,0),其左侧有水平向左的匀强电场E1,MN与y轴之间有沿y轴正方向的匀强电场E2,E1、E2均未知,在第一、三、四象限内有垂直纸面向里的匀强磁场,磁感应强度B未知.现有一质量为m、电荷量为q的负粒子从图中A点静止释放,不计粒子重力,粒子到达MN上的P点是速度为v0,速度方向水平,粒子从y轴上的C点(0,0.5L)与y轴负方向成30°角进入磁场,偏转后从x轴上的D点(图中未画出)垂直x轴穿出磁场并进入MN左侧电场且刚好又击中P点,求:
如图所示,在直角坐标系xOy平面内,第二象限中虚线MN平行于y轴,N点坐标为(-L,0),其左侧有水平向左的匀强电场E1,MN与y轴之间有沿y轴正方向的匀强电场E2,E1、E2均未知,在第一、三、四象限内有垂直纸面向里的匀强磁场,磁感应强度B未知.现有一质量为m、电荷量为q的负粒子从图中A点静止释放,不计粒子重力,粒子到达MN上的P点是速度为v0,速度方向水平,粒子从y轴上的C点(0,0.5L)与y轴负方向成30°角进入磁场,偏转后从x轴上的D点(图中未画出)垂直x轴穿出磁场并进入MN左侧电场且刚好又击中P点,求: 如图所示,平行光滑导轨OPQ、O′P′Q′相距L=0.5m,导轨平面与水平面成θ=53°角,OP段和O′P′段是导电的,PQ段和P′Q′段是绝缘的,在P和P′处固定一个“Π”形导体框abcd,导体框平面与导轨面垂直,面积S=0.3m2.空间存在变化的匀强磁场,方向与导轨平行,与线圈abcd垂直.质量为m=0.02kg、电阻R=0.2Ω的金属棒MN放在两导轨上QQ′处,与PP′的距离x=0.64m,棒与导轨垂直并保持良好接触.t=0时刻,从QQ′无初速度释放金属棒MN,此时匀强磁场方向沿导轨向上(规定为正方向),变化规律为B=0.2-0.8t(T).除金属棒MN外,不计其他电阻.问:(sin53°=0.8,cos53°=0.6,取g=10m/s2)
如图所示,平行光滑导轨OPQ、O′P′Q′相距L=0.5m,导轨平面与水平面成θ=53°角,OP段和O′P′段是导电的,PQ段和P′Q′段是绝缘的,在P和P′处固定一个“Π”形导体框abcd,导体框平面与导轨面垂直,面积S=0.3m2.空间存在变化的匀强磁场,方向与导轨平行,与线圈abcd垂直.质量为m=0.02kg、电阻R=0.2Ω的金属棒MN放在两导轨上QQ′处,与PP′的距离x=0.64m,棒与导轨垂直并保持良好接触.t=0时刻,从QQ′无初速度释放金属棒MN,此时匀强磁场方向沿导轨向上(规定为正方向),变化规律为B=0.2-0.8t(T).除金属棒MN外,不计其他电阻.问:(sin53°=0.8,cos53°=0.6,取g=10m/s2)  如图所示,小球A的质量为m=2kg,固定在L=0.4m的轻细直杆一端,并随杆一起绕杆的另一端O点在竖直在竖直平面内做圆周运动,过最低点时速度为4m/s(不计阻力),求:
如图所示,小球A的质量为m=2kg,固定在L=0.4m的轻细直杆一端,并随杆一起绕杆的另一端O点在竖直在竖直平面内做圆周运动,过最低点时速度为4m/s(不计阻力),求: 如图所示,某同学在跳绳比赛中,1min跳了120次,若每次起跳中有$\frac{4}{5}$时间腾空,该同学体重50kg,则他在跳绳中克服重力做功的平均功率是200W,若他在跳绳的1min内,心脏跳动了60次,每次心跳输送1×10-4m3的血液,其血压(可看做心脏血液压强的平均值)为2×104Pa,则心脏工作的平均功率是2W.
如图所示,某同学在跳绳比赛中,1min跳了120次,若每次起跳中有$\frac{4}{5}$时间腾空,该同学体重50kg,则他在跳绳中克服重力做功的平均功率是200W,若他在跳绳的1min内,心脏跳动了60次,每次心跳输送1×10-4m3的血液,其血压(可看做心脏血液压强的平均值)为2×104Pa,则心脏工作的平均功率是2W.