题目内容
6. 如图所示,小球A的质量为m=2kg,固定在L=0.4m的轻细直杆一端,并随杆一起绕杆的另一端O点在竖直在竖直平面内做圆周运动,过最低点时速度为4m/s(不计阻力),求:
如图所示,小球A的质量为m=2kg,固定在L=0.4m的轻细直杆一端,并随杆一起绕杆的另一端O点在竖直在竖直平面内做圆周运动,过最低点时速度为4m/s(不计阻力),求:(1)过最低点时杆对小球的拉力大小和方向;
(2)过最高点时杆对小球的作用力的大小和方向.
分析 (1)在最低点,小球靠拉力和重力的合力提供向心力,根据牛顿第二定律求出拉力的大小.
(2)根据动能定理求出最高点的速度,根据牛顿第二定律求出杆对小球作用力的大小和方向.
解答 解:(1)在最低点,根据牛顿第二定律得,${F}_{1}-mg=m\frac{{{v}_{1}}^{2}}{L}$,
解得${F}_{1}=mg+m\frac{{{v}_{1}}^{2}}{L}=20+2×\frac{16}{0.4}N$=100N.方向竖直向上.
(2)根据动能定理得,$-mg•2L=\frac{1}{2}m{{v}_{2}}^{2}-\frac{1}{2}m{{v}_{1}}^{2}$,
代入数据解得v2=0m/s,
在最高点,$mg-{F}_{2}=m\frac{{{v}_{2}}^{2}}{L}$,解得F2=20N.方向竖直向上.
答:(1)过最低点时杆对小球的拉力大小为100N,方向竖直向上.
(2)过最高点时杆对小球的作用力大小为20N,方向竖直向上.
点评 解决本题的关键知道小球做圆周运动向心力的来源,结合牛顿第二定律进行求解,基础题.

练习册系列答案
相关题目
17.下列说法中正确的是( )
| A. | 光的干涉说明光是横波 | |
| B. | 自然光在水面反射时,反射光和折射光都是一定程度的偏振光 | |
| C. | 在真空中电磁波的频率越高,传播速度越小 | |
| D. | 在不同惯性系中,光在真空中沿不同方向的传播速度不同 |
14.下列关于物理学史和物理学方法的叙述中,正确的是( )
| A. | 牛顿运用理想实验的方法得出“力不是维持物体运动的原因” | |
| B. | 安培发现了电流周围存在磁场,并总结出电流周围磁场方向的判定方法--右手螺旋定则,也称安培定则 | |
| C. | 在定义电场强度时应用了比值法,因而电场强度和电场力成正比,与试探电荷的电荷量成反比 | |
| D. | 在利用速度-时间图象推导匀变速直线运动位移公式时应用的是微元法 |
15. 如图所示,在场强大小为 E 的匀强电场中,有一个边长为L的正方形区域,正方形的一条边与电场方向平行.质量为m、电荷量绝对值为q的电子从某一条边的中点,以初速度v0射入该区域.初速度的方向垂直指向对边,但电子没有从对边飞出.下列说法正确的是( )
如图所示,在场强大小为 E 的匀强电场中,有一个边长为L的正方形区域,正方形的一条边与电场方向平行.质量为m、电荷量绝对值为q的电子从某一条边的中点,以初速度v0射入该区域.初速度的方向垂直指向对边,但电子没有从对边飞出.下列说法正确的是( )
 如图所示,在场强大小为 E 的匀强电场中,有一个边长为L的正方形区域,正方形的一条边与电场方向平行.质量为m、电荷量绝对值为q的电子从某一条边的中点,以初速度v0射入该区域.初速度的方向垂直指向对边,但电子没有从对边飞出.下列说法正确的是( )
如图所示,在场强大小为 E 的匀强电场中,有一个边长为L的正方形区域,正方形的一条边与电场方向平行.质量为m、电荷量绝对值为q的电子从某一条边的中点,以初速度v0射入该区域.初速度的方向垂直指向对边,但电子没有从对边飞出.下列说法正确的是( )| A. | 电场方向可能与初速度方向相反 | |
| B. | 电场方向可能与初速度方向垂直 | |
| C. | 电子离开该区域时,动能可能为$\frac{1}{2}$mv02 | |
| D. | 电子离开该区域时,动能可能为$\frac{1}{2}$mv02+$\frac{1}{2}$qEL |
13. 以不同的抛射角抛出三个小球A、B、C,三球在空中的运动轨迹如图所示,下列说法中正确的是( )
以不同的抛射角抛出三个小球A、B、C,三球在空中的运动轨迹如图所示,下列说法中正确的是( )
 以不同的抛射角抛出三个小球A、B、C,三球在空中的运动轨迹如图所示,下列说法中正确的是( )
以不同的抛射角抛出三个小球A、B、C,三球在空中的运动轨迹如图所示,下列说法中正确的是( )| A. | A、B、C三球在运动过程中,加速度都相同 | |
| B. | B球的射程最远,所以最迟落地 | |
| C. | A球的射高最大,所以最迟落地 | |
| D. | A、C两球的水平位移相等,所以两球的水平速度分量相等 |
 重庆洋人街有一项惊险刺激的游戏项目高空滑索,游戏者通过绳索悬挂在滑车下,滑车跨在两根钢缆上从高处向下滑去,如图所示.若下滑过程中的某一段可看作人与滑车一起沿钢缆匀速下滑,下滑的速度为15m/s,此段钢缆的倾角为30°,人和滑车的总质量为75kg,空气阻力的大小满足f=kv2,其中v为下滑速度,k为常数,忽略滑车和钢缆间的摩擦,重力加速度取10m/s2,求:
重庆洋人街有一项惊险刺激的游戏项目高空滑索,游戏者通过绳索悬挂在滑车下,滑车跨在两根钢缆上从高处向下滑去,如图所示.若下滑过程中的某一段可看作人与滑车一起沿钢缆匀速下滑,下滑的速度为15m/s,此段钢缆的倾角为30°,人和滑车的总质量为75kg,空气阻力的大小满足f=kv2,其中v为下滑速度,k为常数,忽略滑车和钢缆间的摩擦,重力加速度取10m/s2,求: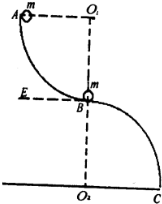 如图所示,有两个完全相同的半径为R的光滑$\frac{1}{4}$圆弧槽,在末端焊接成新的曲线槽ABC,并且固定在竖直面内,使得两个$\frac{1}{4}$圆弧槽所在的圆心O1、O2连线恰好过焊接点B,并垂直于水平地面O2C(且过B处的切线BE恰好为水平线),已知焊接处B也是光滑的,现有两个大小相等,质量均为m的非弹性小球,其中2静止在B点,让球1从曲线槽上端点A由静止开始自由下落,到B处与球2正碰后粘合一起沿槽下滑(已知重力加速度为g)
如图所示,有两个完全相同的半径为R的光滑$\frac{1}{4}$圆弧槽,在末端焊接成新的曲线槽ABC,并且固定在竖直面内,使得两个$\frac{1}{4}$圆弧槽所在的圆心O1、O2连线恰好过焊接点B,并垂直于水平地面O2C(且过B处的切线BE恰好为水平线),已知焊接处B也是光滑的,现有两个大小相等,质量均为m的非弹性小球,其中2静止在B点,让球1从曲线槽上端点A由静止开始自由下落,到B处与球2正碰后粘合一起沿槽下滑(已知重力加速度为g)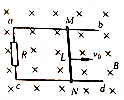 如图所示,两条平行金属导轨ab、cd置于匀强磁场中,磁场方向垂直金属导轨平面,两导轨间的距离L=0.6m,金属杆MN沿两条导轨向右匀速滑动,速度v0=10m/s,产生的感应电动势为3V,已知金属到杆MN的电阻r=1Ω,外接电阻R=8Ω.求:
如图所示,两条平行金属导轨ab、cd置于匀强磁场中,磁场方向垂直金属导轨平面,两导轨间的距离L=0.6m,金属杆MN沿两条导轨向右匀速滑动,速度v0=10m/s,产生的感应电动势为3V,已知金属到杆MN的电阻r=1Ω,外接电阻R=8Ω.求: