题目内容
10. 如图所示,某同学在跳绳比赛中,1min跳了120次,若每次起跳中有$\frac{4}{5}$时间腾空,该同学体重50kg,则他在跳绳中克服重力做功的平均功率是200W,若他在跳绳的1min内,心脏跳动了60次,每次心跳输送1×10-4m3的血液,其血压(可看做心脏血液压强的平均值)为2×104Pa,则心脏工作的平均功率是2W.
如图所示,某同学在跳绳比赛中,1min跳了120次,若每次起跳中有$\frac{4}{5}$时间腾空,该同学体重50kg,则他在跳绳中克服重力做功的平均功率是200W,若他在跳绳的1min内,心脏跳动了60次,每次心跳输送1×10-4m3的血液,其血压(可看做心脏血液压强的平均值)为2×104Pa,则心脏工作的平均功率是2W.
分析 根据每次跳动的时间求出在空中的时间,从而求出上升的最大高度,结合克服重力做功的大小和时间求出平均功率.
根据血压的大小和每次输送血液的体积求出每次心脏做功的大小,从而求出心脏工作的平均功率.
解答 解:跳一次的时间为:${t}_{1}=\frac{60}{120}s=0.5s$,每次在空中的运动时间为:${t}_{2}=\frac{4}{5}{t}_{1}=\frac{4}{5}×0.5s=0.4s$,
则上升的最大高度为:${h}_{m}=\frac{1}{2}g(\frac{{t}_{2}}{2})^{2}=\frac{1}{2}×10×0.04m=0.2m$,
跳绳中克服重力做功的平均功率为:$\overline{P}=\frac{mg{h}_{m}}{{t}_{1}}=\frac{500×0.2}{0.5}W=200W$.
心脏工作的平均功率为:P=$\frac{W}{t}=\frac{60×Psd}{t}=\frac{60×PV}{t}$=$\frac{60×2×1{0}^{4}×1×1{0}^{-4}}{60}W=2W$.
故答案为:200,2.
点评 本题考查了平均功率的基本运用,关键求出功的大小,再结合时间求解平均功率,注意求解克服重力做功的平均功率时,所用的时间包含在地面上的时间.

练习册系列答案
相关题目
20.向平静的水面上抛入一小块石头,在水面上激起一列水波.若将水波视为理想的横波(实际上水波的情况较复杂.不是横波),现观察到水面上漂浮的一片树叶A在开始振动后6s内全振动了3次,当这片树叶开始第6次振动时,沿这列水波传播的方向与该片树叶相距10m、浮在水面上的另一片树叶B刚好开始振动,则( )
| A. | 这列水波的周期是0.5s | B. | 这列水波的波长为$\frac{5}{3}$m | ||
| C. | 这列水波的速度为1.0m/s | D. | 树叶A在l.Os内沿水面运动1.Om |
5.一位同学抱紧一只钢制饭盒由下蹲静止状态起跳再落地过程中,听到盒内一小物块与合壁先后两次撞击的声音,已知盒与人没有相对运动,且盒内只有这个小物块,人跳起过程中尽量上半身竖直,关于这两次撞击,正确的理解是( )
| A. | 盒与人及物块都做相同的竖直上抛运动,小物块不可能撞击盒子的上下壁,一定是由于盒倾斜而引起的撞击 | |
| B. | 一定是小物块大于盒子的初速度而引起的撞击 | |
| C. | 一定是小物块比盒子对地的加速度大而引起的撞击 | |
| D. | 是由于盒子比小物块对地的加速度大而引起的撞击,由于盒子内部高度较小,应该是先撞上壁后撞下壁 |
15. 如图所示,在场强大小为 E 的匀强电场中,有一个边长为L的正方形区域,正方形的一条边与电场方向平行.质量为m、电荷量绝对值为q的电子从某一条边的中点,以初速度v0射入该区域.初速度的方向垂直指向对边,但电子没有从对边飞出.下列说法正确的是( )
如图所示,在场强大小为 E 的匀强电场中,有一个边长为L的正方形区域,正方形的一条边与电场方向平行.质量为m、电荷量绝对值为q的电子从某一条边的中点,以初速度v0射入该区域.初速度的方向垂直指向对边,但电子没有从对边飞出.下列说法正确的是( )
 如图所示,在场强大小为 E 的匀强电场中,有一个边长为L的正方形区域,正方形的一条边与电场方向平行.质量为m、电荷量绝对值为q的电子从某一条边的中点,以初速度v0射入该区域.初速度的方向垂直指向对边,但电子没有从对边飞出.下列说法正确的是( )
如图所示,在场强大小为 E 的匀强电场中,有一个边长为L的正方形区域,正方形的一条边与电场方向平行.质量为m、电荷量绝对值为q的电子从某一条边的中点,以初速度v0射入该区域.初速度的方向垂直指向对边,但电子没有从对边飞出.下列说法正确的是( )| A. | 电场方向可能与初速度方向相反 | |
| B. | 电场方向可能与初速度方向垂直 | |
| C. | 电子离开该区域时,动能可能为$\frac{1}{2}$mv02 | |
| D. | 电子离开该区域时,动能可能为$\frac{1}{2}$mv02+$\frac{1}{2}$qEL |
16. 如图所示,一定质量的理想气体,处在A状态时,温度为tA=27℃,则气体从状态A等容变化到状态M,再等压变化到状态B的过程中,对外所做的功W和在状态B的温度tB分别为(取1atm=1.0×105 Pa)( )
如图所示,一定质量的理想气体,处在A状态时,温度为tA=27℃,则气体从状态A等容变化到状态M,再等压变化到状态B的过程中,对外所做的功W和在状态B的温度tB分别为(取1atm=1.0×105 Pa)( )
 如图所示,一定质量的理想气体,处在A状态时,温度为tA=27℃,则气体从状态A等容变化到状态M,再等压变化到状态B的过程中,对外所做的功W和在状态B的温度tB分别为(取1atm=1.0×105 Pa)( )
如图所示,一定质量的理想气体,处在A状态时,温度为tA=27℃,则气体从状态A等容变化到状态M,再等压变化到状态B的过程中,对外所做的功W和在状态B的温度tB分别为(取1atm=1.0×105 Pa)( )| A. | W=300 J tB=27℃ | B. | W=300 J tB=-33℃ | ||
| C. | W=750 J tB=-33℃ | D. | W=750 J tB=27℃ |
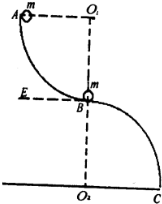 如图所示,有两个完全相同的半径为R的光滑$\frac{1}{4}$圆弧槽,在末端焊接成新的曲线槽ABC,并且固定在竖直面内,使得两个$\frac{1}{4}$圆弧槽所在的圆心O1、O2连线恰好过焊接点B,并垂直于水平地面O2C(且过B处的切线BE恰好为水平线),已知焊接处B也是光滑的,现有两个大小相等,质量均为m的非弹性小球,其中2静止在B点,让球1从曲线槽上端点A由静止开始自由下落,到B处与球2正碰后粘合一起沿槽下滑(已知重力加速度为g)
如图所示,有两个完全相同的半径为R的光滑$\frac{1}{4}$圆弧槽,在末端焊接成新的曲线槽ABC,并且固定在竖直面内,使得两个$\frac{1}{4}$圆弧槽所在的圆心O1、O2连线恰好过焊接点B,并垂直于水平地面O2C(且过B处的切线BE恰好为水平线),已知焊接处B也是光滑的,现有两个大小相等,质量均为m的非弹性小球,其中2静止在B点,让球1从曲线槽上端点A由静止开始自由下落,到B处与球2正碰后粘合一起沿槽下滑(已知重力加速度为g)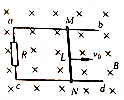 如图所示,两条平行金属导轨ab、cd置于匀强磁场中,磁场方向垂直金属导轨平面,两导轨间的距离L=0.6m,金属杆MN沿两条导轨向右匀速滑动,速度v0=10m/s,产生的感应电动势为3V,已知金属到杆MN的电阻r=1Ω,外接电阻R=8Ω.求:
如图所示,两条平行金属导轨ab、cd置于匀强磁场中,磁场方向垂直金属导轨平面,两导轨间的距离L=0.6m,金属杆MN沿两条导轨向右匀速滑动,速度v0=10m/s,产生的感应电动势为3V,已知金属到杆MN的电阻r=1Ω,外接电阻R=8Ω.求: 如图所示,圆形区域内分布着垂直纸面的匀强磁场,位于磁场边界上P点的粒子源在纸面内沿各个方向以相同的速率向磁场发射同种带电粒子,这些粒子射出边界的位置均分布在边界的某一段弧上,且这段圆弧的弧长是圆周长的$\frac{1}{3}$;若将磁感应强度的大小从B1变为B2,相应的弧长变为圆周长的$\frac{1}{6}$,则$\frac{{B}_{2}}{{B}_{1}}$等于( )
如图所示,圆形区域内分布着垂直纸面的匀强磁场,位于磁场边界上P点的粒子源在纸面内沿各个方向以相同的速率向磁场发射同种带电粒子,这些粒子射出边界的位置均分布在边界的某一段弧上,且这段圆弧的弧长是圆周长的$\frac{1}{3}$;若将磁感应强度的大小从B1变为B2,相应的弧长变为圆周长的$\frac{1}{6}$,则$\frac{{B}_{2}}{{B}_{1}}$等于( )