题目内容
15.两靠得较近的天体组成的系统称为双星,它们以两者连线上某点为圆心做匀速圆周运动,因而不至于由于引力作用而吸引在一起.设两天体的质量分别为m1和m2,则它们的轨道半径之比Rm1:Rm2=m2:m1,速度之比vm1:vm2=m2:m1.分析 双星靠相互间的万有引力提供向心力,抓住角速度相等,向心力相等求出轨道半径之比;根据万有引力提供向心力求出角速度的大小
解答 解:(1)设m1和m2的轨道半径分别为r1,r2 角速度为ω,由万有引力定律和向心力公式:G$\frac{{m}_{1}{m}_{2}}{{L}^{2}}$=m1ω2r1=m2ω2r2,
得:r1 :r2=m2:m1.
由v=rω得:vm1:vm2=m2:m1
故答案为:m2:m1,m2:m1
点评 解决本题的关键掌握双星模型系统,知道它们靠相互间的万有引力提供向心力,向心力的大小相等,角速度的大小相等

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
3. 如图,长为h的水银柱将上端封闭的玻璃管内气体分隔成两部分,A处管内外水银面相平.将玻璃管缓慢向上提升H高度(管下端未离开水银面),上下两部分气体的压强变化分别为△p1和△p2,体积变化分别为△V1和△V2.已知水银密度为ρ,玻璃管截面积为S,则( )
如图,长为h的水银柱将上端封闭的玻璃管内气体分隔成两部分,A处管内外水银面相平.将玻璃管缓慢向上提升H高度(管下端未离开水银面),上下两部分气体的压强变化分别为△p1和△p2,体积变化分别为△V1和△V2.已知水银密度为ρ,玻璃管截面积为S,则( )
 如图,长为h的水银柱将上端封闭的玻璃管内气体分隔成两部分,A处管内外水银面相平.将玻璃管缓慢向上提升H高度(管下端未离开水银面),上下两部分气体的压强变化分别为△p1和△p2,体积变化分别为△V1和△V2.已知水银密度为ρ,玻璃管截面积为S,则( )
如图,长为h的水银柱将上端封闭的玻璃管内气体分隔成两部分,A处管内外水银面相平.将玻璃管缓慢向上提升H高度(管下端未离开水银面),上下两部分气体的压强变化分别为△p1和△p2,体积变化分别为△V1和△V2.已知水银密度为ρ,玻璃管截面积为S,则( )| A. | △p2一定等于△p1 | B. | △V2一定等于△V1 | ||
| C. | △p2与△p1之差为ρgh | D. | △V2与△V2之和为HS |
2.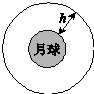 我国已相继完成“神十”与“天宫”对接、“嫦娥”携“玉兔”落月两大航天工程.某航天爱好者提出“玉兔”回家的设想:如图所示,将携带“玉兔”的返回系统由月球表面发射到h高度的轨道上,与在该轨道绕月球做圆周运动的飞船对接,然后由飞船送“玉兔”返回地球.设“玉兔”质量为m,月球半径为R,月面的重力加速度为g月.以月面为零势能面,“玉兔”在h高度的引力势能可表示为Ep=$\frac{GMmh}{R(R+h)}$,其中G为引力常量,M为月球质量.若忽略月球的自转,从开始发射到对接完成需要对“玉兔”做的功为( )
我国已相继完成“神十”与“天宫”对接、“嫦娥”携“玉兔”落月两大航天工程.某航天爱好者提出“玉兔”回家的设想:如图所示,将携带“玉兔”的返回系统由月球表面发射到h高度的轨道上,与在该轨道绕月球做圆周运动的飞船对接,然后由飞船送“玉兔”返回地球.设“玉兔”质量为m,月球半径为R,月面的重力加速度为g月.以月面为零势能面,“玉兔”在h高度的引力势能可表示为Ep=$\frac{GMmh}{R(R+h)}$,其中G为引力常量,M为月球质量.若忽略月球的自转,从开始发射到对接完成需要对“玉兔”做的功为( )
 我国已相继完成“神十”与“天宫”对接、“嫦娥”携“玉兔”落月两大航天工程.某航天爱好者提出“玉兔”回家的设想:如图所示,将携带“玉兔”的返回系统由月球表面发射到h高度的轨道上,与在该轨道绕月球做圆周运动的飞船对接,然后由飞船送“玉兔”返回地球.设“玉兔”质量为m,月球半径为R,月面的重力加速度为g月.以月面为零势能面,“玉兔”在h高度的引力势能可表示为Ep=$\frac{GMmh}{R(R+h)}$,其中G为引力常量,M为月球质量.若忽略月球的自转,从开始发射到对接完成需要对“玉兔”做的功为( )
我国已相继完成“神十”与“天宫”对接、“嫦娥”携“玉兔”落月两大航天工程.某航天爱好者提出“玉兔”回家的设想:如图所示,将携带“玉兔”的返回系统由月球表面发射到h高度的轨道上,与在该轨道绕月球做圆周运动的飞船对接,然后由飞船送“玉兔”返回地球.设“玉兔”质量为m,月球半径为R,月面的重力加速度为g月.以月面为零势能面,“玉兔”在h高度的引力势能可表示为Ep=$\frac{GMmh}{R(R+h)}$,其中G为引力常量,M为月球质量.若忽略月球的自转,从开始发射到对接完成需要对“玉兔”做的功为( )| A. | $\frac{m{g}_{月}R}{R+h}$(h+2R) | B. | $\frac{m{g}_{月}R}{R+h}$(h+$\sqrt{2}$R) | C. | $\frac{m{g}_{月}R}{R+h}$(h+$\frac{\sqrt{2}}{2}$R) | D. | $\frac{m{g}_{月}R}{R+h}$(h+$\frac{1}{2}$R) |
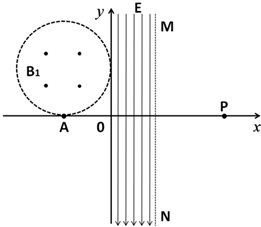 如图所示,第二象限,半径为r的圆形区域内存在方向垂直纸面向外的匀强磁场,磁场边界恰好与两坐标轴相切.x轴上切点A处有一粒子源,能个向x轴上方发射速率相等,均为v,质量为m,电量为+q的粒子,粒子重力不计.圆形区域磁场的磁感应强度B1=$\frac{mv}{qr}$,y轴右侧0<y<r的范围内存在沿y轴负方向的匀强电场,已知某粒子从A处沿+y方向射入磁场后,再进入匀强电场,发现粒子从电场右边界MN射出,速度方向与x轴正方向成45°角斜向下,求:
如图所示,第二象限,半径为r的圆形区域内存在方向垂直纸面向外的匀强磁场,磁场边界恰好与两坐标轴相切.x轴上切点A处有一粒子源,能个向x轴上方发射速率相等,均为v,质量为m,电量为+q的粒子,粒子重力不计.圆形区域磁场的磁感应强度B1=$\frac{mv}{qr}$,y轴右侧0<y<r的范围内存在沿y轴负方向的匀强电场,已知某粒子从A处沿+y方向射入磁场后,再进入匀强电场,发现粒子从电场右边界MN射出,速度方向与x轴正方向成45°角斜向下,求: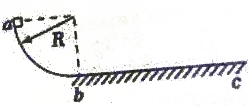 如图所示,质量为m的物块在光滑的$\frac{1}{4}$圆弧轨道的顶端a点由静止开始下滑,圆弧轨道半径为R,最低点b与粗糙水平轨道想接,物块最终滑至c点停止,bc间距为S,求:
如图所示,质量为m的物块在光滑的$\frac{1}{4}$圆弧轨道的顶端a点由静止开始下滑,圆弧轨道半径为R,最低点b与粗糙水平轨道想接,物块最终滑至c点停止,bc间距为S,求:
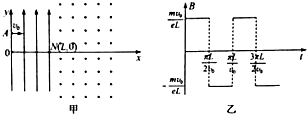
 一质量为m、电荷量为q的带正电粒子(重力不计),以初速度v0进入电势差为U的带窄缝的平行板电极S1和S2间的电场,经电场加速后,沿OX方向进入磁感应强度为B、方向垂直纸面向外的有界匀强磁场,OX垂直平板电极S2.当粒子从p点离开磁场时,其速度方向与OX方向的夹角θ=60°,整个装置处于真空中,如图所示.求:
一质量为m、电荷量为q的带正电粒子(重力不计),以初速度v0进入电势差为U的带窄缝的平行板电极S1和S2间的电场,经电场加速后,沿OX方向进入磁感应强度为B、方向垂直纸面向外的有界匀强磁场,OX垂直平板电极S2.当粒子从p点离开磁场时,其速度方向与OX方向的夹角θ=60°,整个装置处于真空中,如图所示.求: