题目内容
18.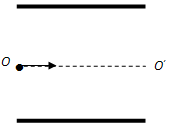 如图所示,长为L两极板水平放置,其间距也为L.一个质量为m,电荷量为q的带正电的粒子,以某一初速度沿中轴线OO′射入两板间.若两板间只存 在竖直向下的匀强电场(图中未画出),粒子射出时的速度为v方向与OO′的夹角450.若两板间只存在垂直纸面向里的匀强磁场,粒子仍以原来的初速度沿中轴线OO′射入,射出的方向与OO′的夹角为30°(图中未画出).不计粒子的重力,求:
如图所示,长为L两极板水平放置,其间距也为L.一个质量为m,电荷量为q的带正电的粒子,以某一初速度沿中轴线OO′射入两板间.若两板间只存 在竖直向下的匀强电场(图中未画出),粒子射出时的速度为v方向与OO′的夹角450.若两板间只存在垂直纸面向里的匀强磁场,粒子仍以原来的初速度沿中轴线OO′射入,射出的方向与OO′的夹角为30°(图中未画出).不计粒子的重力,求:(1)所加匀强电场的电场强度.
(2)所加匀强磁场的磁感应强度.
(3)若上述的电场、磁场同时存在,欲使粒子沿OO′直线通过,粒子入射的初速的大小.
分析 (1)两极板间只存在竖直向下的匀强电场时,粒子在电场中做类平抛运动,根据运动的合成与分解,分解为水平方向的匀速运动和竖直方向的匀加速运动,将射出速度分解为水平和竖直方向,水平分速度即为${v}_{0}^{\;}$,竖直分速度为${v}_{y}^{\;}$,根据牛顿第二定律求加速度,时间t=$\frac{L}{{v}_{0}^{\;}}$,${v}_{y}^{\;}=at$,联立即可求出E;
(2)板间只存在垂直纸面向里的匀强磁场时,粒子做匀速圆周运动,根据几何关系求出半径,洛伦兹力提供向心力得出半径公式,即可求出B;
(3)电场、磁场同时存在,欲使粒子沿OO′直线通过,则电场力和洛伦兹力平衡,即可求出粒子入射的初速的大小
解答 解:(1)粒子在电场中做类平抛运动,将射出速度v分解为水平和竖直分速度
初速度${v}_{0}^{\;}=vcos45°=\frac{\sqrt{2}}{2}v$
竖直分速度${v}_{y}^{\;}=vsin45°=\frac{\sqrt{2}}{2}v$
根据牛顿第二定律,加速度$a=\frac{Eq}{m}$
运动时间$t=\frac{L}{{v}_{0}^{\;}}=\frac{L}{\frac{\sqrt{2}}{2}v}=\frac{\sqrt{2}L}{v}$
竖直速度${v}_{y}^{\;}=at$
联立得$\frac{\sqrt{2}}{2}v=\frac{Eq}{m}•\frac{\sqrt{2}L}{v}$
解得:$E=\frac{m{v}_{\;}^{2}}{2qL}$
(2)板间只存在垂直纸面向里的匀强磁场时,粒子做匀速圆周运动
根据几何关系有$sin30°=\frac{L}{R}$
即R=2L
由洛伦兹力提供向心力,有
$q{v}_{0}^{\;}B=m\frac{{v}_{0}^{2}}{R}$
得$R=\frac{m{v}_{0}^{\;}}{qB}$
$B=\frac{m{v}_{0}^{\;}}{qR}=\frac{m\frac{\sqrt{2}}{2}v}{q•2L}=\frac{\sqrt{2}mv}{4qL}$
(3)若上述的电场、磁场同时存在,欲使粒子沿OO′直线通过,则有
$q{v}_{0}^{′}B=Eq$
解得:${v}_{0}^{′}=\frac{E}{B}=\sqrt{2}v$
答:(1)所加匀强电场的电场强度为$\frac{m{v}_{\;}^{2}}{2qL}$.
(2)所加匀强磁场的磁感应强度为$\frac{\sqrt{2}mv}{4qL}$.
(3)若上述的电场、磁场同时存在,欲使粒子沿OO′直线通过,粒子入射的初速的大小为$\sqrt{2}v$
点评 带电粒子在电场中运动分为加速和偏转两种类型,常运用动能定理和平抛运动规律求解,注意运算时要细心,而在匀强磁场中运动时,重要的是由运动径迹利用几何关系找到半径的大小,由洛伦兹力提供向心力,利用牛顿第二定律求解即可

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
| A. | 弹簧测力计的示数是30N | |
| B. | 弹簧测力计的示数是18N | |
| C. | 在突然撤去F的瞬间,弹簧测力计的示数为零 | |
| D. | 在突然撤去F的瞬间,m1的加速度9m/s2 |
 如图所示,斜面AD、BD动摩擦因数相同.可视为质点的物体,分别沿AD、BD从斜面顶端由静止下滑到底端,下列说法正确的是( )
如图所示,斜面AD、BD动摩擦因数相同.可视为质点的物体,分别沿AD、BD从斜面顶端由静止下滑到底端,下列说法正确的是( )| A. | 物体沿AD比沿BD斜面滑动到底端时合力做功多 | |
| B. | 物体沿AD比沿BD斜面滑动到底端时动能大 | |
| C. | 物体沿AD比沿BD斜面滑动到底端过程中克服摩擦力做的功多 | |
| D. | 物体沿AD比沿BD斜面滑动到底端过程中克服摩擦力做的功少 |

| A. | 振源振动的频率是4Hz | B. | 波沿x轴正向传播 | ||
| C. | 波的传播速度大小为1m/s | D. | t=2s时,质点P到达x=4m处 |
| A. | 运动员在第1s末的速度是8m/s | |
| B. | 运动员在第7s内的平均速度是9m/s | |
| C. | 运动员在第7s末的瞬时速度是9m/s | |
| D. | 运动员在百米比赛中的平均速度为8m/s |
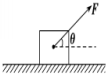 质量为m=2kg的物体,静止放在水平面上,它们之间的动摩擦因数μ=0.5,现对物体施加F=20N的作用力,方向与水平面成θ=37°角斜向上,如图所示,(sin 37°=0.6,cos37°=0.80,g取10m/s2)求:
质量为m=2kg的物体,静止放在水平面上,它们之间的动摩擦因数μ=0.5,现对物体施加F=20N的作用力,方向与水平面成θ=37°角斜向上,如图所示,(sin 37°=0.6,cos37°=0.80,g取10m/s2)求:
 如图,一长L为1.25m的细绳,一端固定于O点,另一端系一个质量m1为0.2kg的小球.当球在竖直方向静止时,球对水平桌面的作用力刚好为零.现将球提起使细绳处于水平位置时无初速释放.当球m1摆至最低点时,恰与放在桌面上的质量m2为0.8kg的小物块正碰,碰后m1小球以2m/s的速度弹回.m2将沿水平桌面运动,已知小物块与桌面间动摩擦因数为μ=0.1;g=l0m/s2,求:
如图,一长L为1.25m的细绳,一端固定于O点,另一端系一个质量m1为0.2kg的小球.当球在竖直方向静止时,球对水平桌面的作用力刚好为零.现将球提起使细绳处于水平位置时无初速释放.当球m1摆至最低点时,恰与放在桌面上的质量m2为0.8kg的小物块正碰,碰后m1小球以2m/s的速度弹回.m2将沿水平桌面运动,已知小物块与桌面间动摩擦因数为μ=0.1;g=l0m/s2,求: