题目内容
19. 如图所示,竖直平面内固定有一个半径为R的四分之一圆弧轨道PQ,其中半径OP水平、OQ竖直,现从圆心O处以某一初速度水平抛出一小球,小球经时间t=$\sqrt{\frac{R}{g}}$落到了圆轨道上,不计空气阻力,重力加速度为g.求小球平抛的初速度v0.
如图所示,竖直平面内固定有一个半径为R的四分之一圆弧轨道PQ,其中半径OP水平、OQ竖直,现从圆心O处以某一初速度水平抛出一小球,小球经时间t=$\sqrt{\frac{R}{g}}$落到了圆轨道上,不计空气阻力,重力加速度为g.求小球平抛的初速度v0.
分析 小球做平抛运动,已知运动的时间,根据竖直分运动公式求解竖直分位移,结合几何关系得到水平分位移,最后根据水平分位移公式求解初速度.
解答 解:小球做平抛运动,如图所示,根据分位移公式,有:
竖直方向:y=$\frac{1}{2}$gt2=$\frac{1}{2}$R
水平方向:x=$\sqrt{{R}^{2}-{y}^{2}}$=$\frac{\sqrt{3}}{2}$R
平抛的初速度v0=$\frac{x}{t}$=$\frac{\sqrt{3gR}}{2}$
答:小球平抛的初速度v0为$\frac{\sqrt{3gR}}{2}$.
点评 本题关键是根据平抛运动的分位移公式列式求解,基础题目.

练习册系列答案
相关题目
17. 如图所示电路中L1发光,L2、L3不亮,
如图所示电路中L1发光,L2、L3不亮, 有读数,
有读数, 没有读数,则产生的故障应是( )(只有一处有故障)
没有读数,则产生的故障应是( )(只有一处有故障)
 如图所示电路中L1发光,L2、L3不亮,
如图所示电路中L1发光,L2、L3不亮, 有读数,
有读数, 没有读数,则产生的故障应是( )(只有一处有故障)
没有读数,则产生的故障应是( )(只有一处有故障)| A. | 灯泡L1断路 | B. | 灯泡L2断路 | C. | 灯泡L3短路 | D. | 灯泡L2短路 |
10.图甲为一列简谐横波在t=0.7s时刻的波形图,图乙为质点P的振动图象,则下列说法正确的是( )
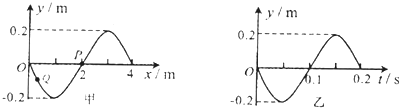

| A. | 波速v=20m/s,向右传播 | |
| B. | 波速v=20m/s,向左传播 | |
| C. | 从t=0.7s时刻开始,再经0.15s,波向左传播了3m | |
| D. | 从t=0.7s时刻开始,再经0.15s,质点P向左运动了3m |
14.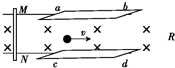 如图所示,ab、cd为水平平行金属板,两板左端与光滑平行金属轨道相连接,金属轨道在竖直平面内,匀强磁场垂直于轨道平面,磁感应强度为B.一质量为m、带电荷量为-q的液滴可在两板间以速率v向右做匀速直线运动,则导体棒MN的运动.
如图所示,ab、cd为水平平行金属板,两板左端与光滑平行金属轨道相连接,金属轨道在竖直平面内,匀强磁场垂直于轨道平面,磁感应强度为B.一质量为m、带电荷量为-q的液滴可在两板间以速率v向右做匀速直线运动,则导体棒MN的运动.
 如图所示,ab、cd为水平平行金属板,两板左端与光滑平行金属轨道相连接,金属轨道在竖直平面内,匀强磁场垂直于轨道平面,磁感应强度为B.一质量为m、带电荷量为-q的液滴可在两板间以速率v向右做匀速直线运动,则导体棒MN的运动.
如图所示,ab、cd为水平平行金属板,两板左端与光滑平行金属轨道相连接,金属轨道在竖直平面内,匀强磁场垂直于轨道平面,磁感应强度为B.一质量为m、带电荷量为-q的液滴可在两板间以速率v向右做匀速直线运动,则导体棒MN的运动.| A. | 速率为$\frac{mg}{qB}$,方向向左 | B. | 速率为$\frac{mg}{qB}$,方向向右 | ||
| C. | 速率为v-$\frac{mg}{qB}$,方向向右 | D. | 速率为v+$\frac{mg}{qB}$,方向向右 |
4.将一物块竖直向上抛出,物块在空中由A点运动到B点的过程中,受重力和空气阻力作用,若重力做功-3J,空气阻力做功-1J,则物块的( )
| A. | 重力势能增加3J | B. | 重力势能减少3J | C. | 动能减少1J | D. | 机械能减少1J |
11. 如图所示,质量为M、半径为R的半球形物体A放在水平地面上,通过最高点处的钉子用水平细线拉住一质量为m、半径为r的光滑球B.现整个系统处于静止状态,则( )
如图所示,质量为M、半径为R的半球形物体A放在水平地面上,通过最高点处的钉子用水平细线拉住一质量为m、半径为r的光滑球B.现整个系统处于静止状态,则( )
 如图所示,质量为M、半径为R的半球形物体A放在水平地面上,通过最高点处的钉子用水平细线拉住一质量为m、半径为r的光滑球B.现整个系统处于静止状态,则( )
如图所示,质量为M、半径为R的半球形物体A放在水平地面上,通过最高点处的钉子用水平细线拉住一质量为m、半径为r的光滑球B.现整个系统处于静止状态,则( )| A. | A对地面没有摩擦力 | B. | A对地面的摩擦力方向向左 | ||
| C. | B对A的压力大小为$\frac{R+r}{R}$mg | D. | 细线对小球的拉力大小为$\frac{r}{R}$mg |
8. 回旋加速器是加速带电粒子的装置.其主体部分是两个“D”形金属盒,两金属盒处于垂直于盒底的匀强磁场中,并分别与高频交流电源的两极相连接,从而使粒子每次经过两盒间的狭缝时都得到加速,如图所示.对于其原理的分析,下列说法正确的是( )
回旋加速器是加速带电粒子的装置.其主体部分是两个“D”形金属盒,两金属盒处于垂直于盒底的匀强磁场中,并分别与高频交流电源的两极相连接,从而使粒子每次经过两盒间的狭缝时都得到加速,如图所示.对于其原理的分析,下列说法正确的是( )
 回旋加速器是加速带电粒子的装置.其主体部分是两个“D”形金属盒,两金属盒处于垂直于盒底的匀强磁场中,并分别与高频交流电源的两极相连接,从而使粒子每次经过两盒间的狭缝时都得到加速,如图所示.对于其原理的分析,下列说法正确的是( )
回旋加速器是加速带电粒子的装置.其主体部分是两个“D”形金属盒,两金属盒处于垂直于盒底的匀强磁场中,并分别与高频交流电源的两极相连接,从而使粒子每次经过两盒间的狭缝时都得到加速,如图所示.对于其原理的分析,下列说法正确的是( )| A. | 电场和磁场都对粒子起到一定的加速作用 | |
| B. | 用同样的交变电源对不同比荷的粒子加速时,磁感应强度应不同 | |
| C. | 增大高频交流电压,可增大加速粒子的最后的动能 | |
| D. | 增大金属盒的半径,可增大加速粒子的最后的动能 |
 如图所示的装置叫做阿特伍德机,是阿特伍德创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.绳子两端的物体下落(上升)的加速度总是小于自由落体的加速度g,同自由落体相比,下落相同的高度,所花费的时间要长,这使得实验者有足够的时间从容的观测、研究.已知物体A、B的质量相等均为M,物体C的质量为m,轻绳与轻滑轮间的摩擦不计,轻绳不可伸长且足够长,如果M=4m,求:
如图所示的装置叫做阿特伍德机,是阿特伍德创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.绳子两端的物体下落(上升)的加速度总是小于自由落体的加速度g,同自由落体相比,下落相同的高度,所花费的时间要长,这使得实验者有足够的时间从容的观测、研究.已知物体A、B的质量相等均为M,物体C的质量为m,轻绳与轻滑轮间的摩擦不计,轻绳不可伸长且足够长,如果M=4m,求: 如图所示,光滑水平平台MN的左端M处有一弹射装置P,右端N与水平传送带相接,传送带沿逆时针方向以v=2m/s匀速转动,水平部分长L=9m.放在MN段有一质量为m的滑块A以初速度v0=4m/s冲上传送带,结果滑块滑上传送带运动一段时间后,又返回N端,经水平面与左端M处的固定弹射器P相碰撞(弹射器P的弹簧原来被压缩后锁定),滑块挨到弹射器时弹射器立即解锁,滑块被弹射器弹回且再次滑上传送带.已知滑块与传送带间的动摩擦因数μ=0.2,滑块的质量m=1kg,取g=10m/s2.求:
如图所示,光滑水平平台MN的左端M处有一弹射装置P,右端N与水平传送带相接,传送带沿逆时针方向以v=2m/s匀速转动,水平部分长L=9m.放在MN段有一质量为m的滑块A以初速度v0=4m/s冲上传送带,结果滑块滑上传送带运动一段时间后,又返回N端,经水平面与左端M处的固定弹射器P相碰撞(弹射器P的弹簧原来被压缩后锁定),滑块挨到弹射器时弹射器立即解锁,滑块被弹射器弹回且再次滑上传送带.已知滑块与传送带间的动摩擦因数μ=0.2,滑块的质量m=1kg,取g=10m/s2.求: