题目内容
7. 如图所示,长为L的细绳一端固定于O点,另一端系一个质量为m的小球,将细绳在水平方向拉直,从静止状态释放小球,小球运动到最低点时速度大小为v,细绳拉力为F,小球的向心加速度为a,则下列说法正确的是( )
如图所示,长为L的细绳一端固定于O点,另一端系一个质量为m的小球,将细绳在水平方向拉直,从静止状态释放小球,小球运动到最低点时速度大小为v,细绳拉力为F,小球的向心加速度为a,则下列说法正确的是( )| A. | 小球质量变为2m,其他条件不变,则小球到最低点的速度为v | |
| B. | 小球质量变为2m,其他条件不变,则小球到最低点时细绳拉力变为2F | |
| C. | 细绳长度变为2L,其他条件不变,小球到最低点时向心加速度变为2a | |
| D. | 细绳长度变为2L,其他条件不变,小球到最低点时向心加速度为a |
分析 根据动能定理得出最低点的速度,判断是否与小球的质量有关.根据牛顿第二定理得出拉力的表达式,结合质量的变化判断拉力的变化.根据向心加速度公式得出向心加速度的大小,判断是否与细线的长度有关.
解答 解:A、根据动能定理得,$mgL=\frac{1}{2}m{v}^{2}$,解得小球到达最低点的速度v=$\sqrt{2gL}$,与小球的质量无关,所以小球质量变为2m,其他条件不变,则小球到最低点的速度为v,故A正确.
B、小球质量变为2m,到达最低点的速度不变,仍然为v,根据牛顿第二定理得,$F-2mg=2m\frac{{v}^{2}}{r}$,解得F=2mg+$2m\frac{{v}^{2}}{r}$,可知拉力变为2F,故B正确.
C、到达最低点的向心加速度a=$\frac{{v}^{2}}{L}=2g$,与细线的长度无关,故C错误,D正确.
故选:ABD.
点评 该题是动能定理及圆周运动向心力公式的直接应用,要求某个量的变化是否会引起另一个量的变化,最后先求出该量的函数表达式,难度适中.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
1.以下情景描述不符合物理实际的是( )
| A. | 火车轨道在弯道处设计成外轨高内轨低,以便火车成功的转弯 | |
| B. | 汽车通过拱形桥最高点时对桥的压力小于汽车重力,但汽车通过凹面时超重 | |
| C. | 在轨道上飞行的航天器中的物体处于“完全失重状态”,悬浮的液滴是平衡状态 | |
| D. | 离心趋势也是可以利用的,洗衣机脱水时利用离心运动把附着在衣物上的水份甩掉 |
15.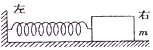 如图所示,物块的质量为m,它与水平桌面间的动摩擦因数为μ.起初,用手按住物块,物块的速度为零,弹簧的伸长量为x.然后放手,当弹簧第一次恢复原长时,物块的速度为v.则此过程中弹力所做的功为( )
如图所示,物块的质量为m,它与水平桌面间的动摩擦因数为μ.起初,用手按住物块,物块的速度为零,弹簧的伸长量为x.然后放手,当弹簧第一次恢复原长时,物块的速度为v.则此过程中弹力所做的功为( )
 如图所示,物块的质量为m,它与水平桌面间的动摩擦因数为μ.起初,用手按住物块,物块的速度为零,弹簧的伸长量为x.然后放手,当弹簧第一次恢复原长时,物块的速度为v.则此过程中弹力所做的功为( )
如图所示,物块的质量为m,它与水平桌面间的动摩擦因数为μ.起初,用手按住物块,物块的速度为零,弹簧的伸长量为x.然后放手,当弹簧第一次恢复原长时,物块的速度为v.则此过程中弹力所做的功为( )| A. | $\frac{1}{2}$mv2+μmgx | B. | $\frac{1}{2}$mv2-μmgx | C. | μmgx-$\frac{1}{2}$mv2 | D. | 以上选项均不对 |
2.为使列车行驶安全,在修建铁路时,转弯处的轨道平面并不是修成水平面,而是使内外轨道间形成一定的高度差,对它的作用有下列说法,正确的是( )
| A. | 这可使列车转弯时不需要向心力 | |
| B. | 这可使列车转弯时车轮不对内、外铁轨产生任何侧向的挤压 | |
| C. | 这可使列车转弯时车轮减小或者不对外轨产生侧向的挤压 | |
| D. | 这可使列车转弯时车轮减小或者不对内轨产生侧向的挤压 |
17.在α粒子散射实验中,少数α粒子发生了大角度偏转,这些α粒子( )
| A. | 一直受到重金属原子核的斥力作用 | |
| B. | 动能不断减小 | |
| C. | 电势能先增大后减小 | |
| D. | 出现大角度偏转是与电子碰撞的结果 |
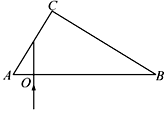 如图所示为一直角棱镜的截面图,∠ACB=90°,∠CAB=60°,AC边长为L.一平行细光束从AB面上的O点沿垂直于AB面的方向射入棱镜,经AC面的中点 P反射后,在BC面上的M点同时发生反射和折射,且反射光线和折射光线互相垂直(P点和M点图中未画出),反射光线从AB面的O'射出,已知光在真空中的传播速度为c,求:
如图所示为一直角棱镜的截面图,∠ACB=90°,∠CAB=60°,AC边长为L.一平行细光束从AB面上的O点沿垂直于AB面的方向射入棱镜,经AC面的中点 P反射后,在BC面上的M点同时发生反射和折射,且反射光线和折射光线互相垂直(P点和M点图中未画出),反射光线从AB面的O'射出,已知光在真空中的传播速度为c,求: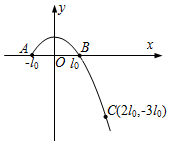 如图所示,在xOy平面内,将质量为m的小物体(可看成质点)以一定速度从A点斜向上抛出,B和C是粒子运动轨迹上的两点,如图所示,其中l0为常数,忽略空气阻力,求:
如图所示,在xOy平面内,将质量为m的小物体(可看成质点)以一定速度从A点斜向上抛出,B和C是粒子运动轨迹上的两点,如图所示,其中l0为常数,忽略空气阻力,求: 两个等高的水平圆盘通过皮带传动(皮带不打滑),各自绕中心轴O1、O2匀速转动,俯视图如图所示,圆盘半径分别为R=0.60m,r=0.40m.一小物体放置于大圆盘的盘面上,与圆心O1的距离为x=0.45m,与圆盘的动摩擦因数μa=0.25.设最大静摩擦力和滑动摩擦力相等,重力加速度g取9.8m/s2.要使物体相对圆盘O1静止,圆盘O2的角速度最大是多少?
两个等高的水平圆盘通过皮带传动(皮带不打滑),各自绕中心轴O1、O2匀速转动,俯视图如图所示,圆盘半径分别为R=0.60m,r=0.40m.一小物体放置于大圆盘的盘面上,与圆心O1的距离为x=0.45m,与圆盘的动摩擦因数μa=0.25.设最大静摩擦力和滑动摩擦力相等,重力加速度g取9.8m/s2.要使物体相对圆盘O1静止,圆盘O2的角速度最大是多少?