题目内容
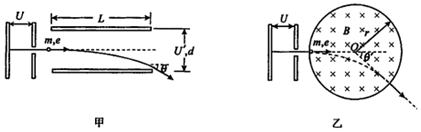
2. 如图所示为一直角棱镜的截面图,∠ACB=90°,∠CAB=60°,AC边长为L.一平行细光束从AB面上的O点沿垂直于AB面的方向射入棱镜,经AC面的中点 P反射后,在BC面上的M点同时发生反射和折射,且反射光线和折射光线互相垂直(P点和M点图中未画出),反射光线从AB面的O'射出,已知光在真空中的传播速度为c,求:
如图所示为一直角棱镜的截面图,∠ACB=90°,∠CAB=60°,AC边长为L.一平行细光束从AB面上的O点沿垂直于AB面的方向射入棱镜,经AC面的中点 P反射后,在BC面上的M点同时发生反射和折射,且反射光线和折射光线互相垂直(P点和M点图中未画出),反射光线从AB面的O'射出,已知光在真空中的传播速度为c,求:①该棱镜的折射率;
②光在棱镜中传播时从O点到O'点所用的时间.
分析 ①画出光路图,确定出光线在BC边上的入射角和折射角,再求该棱镜的折射率;
②由v=$\frac{c}{n}$求得光线在棱镜中的传播速度,由几何知识求出光线在棱镜中传播的距离,即可求得光在棱镜中传播时从O点到O'点所用的时间.
解答  解:①从O点射入棱镜后,光路图如图所示:
解:①从O点射入棱镜后,光路图如图所示:
由反射定律可知 α1=α1′=60°
由于两法线互相垂直,故α2=α2′=30°
可知在M点反射光线与入射光线平行,由题可知 β=60°
在BC面,由折射定律可知,$\frac{sin{α}_{2}′}{sinβ}$=$\frac{1}{n}$,解得 n=$\sqrt{3}$
②由几何关系可知从O点到O'点光通过的路程为
x=OP+PM+MO′=$\frac{Lsin{α}_{1}}{2}$+$\frac{L}{2sin{α}_{1}′}$+$\frac{1}{2}(\sqrt{3}L-\frac{L}{2sin{α}_{1}′})$sin30°
代入数据得 x=$\frac{3\sqrt{3}}{4}$L
又光在介质中的传播速度为 v=$\frac{c}{n}$
代入解得 t=$\frac{9L}{4c}$
答:①该棱镜的折射率是$\sqrt{3}$;
②光在棱镜中传播时从O点到O'点所用的时间是$\frac{9L}{4c}$.
点评 本题是几何光学问题,要能熟练运用光的折射定律、反射定律,还要利用光的几何特性,来寻找角与角的关系,从而算出结果.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
13. 如图所示:直导线MN放置在闭合线圈上且相互绝缘,导线到圆心的距离为d.在导线中通入一个电流I,若要使线圈中产生一个顺时针的电流,导线中的电流方向和大小可能是( )
如图所示:直导线MN放置在闭合线圈上且相互绝缘,导线到圆心的距离为d.在导线中通入一个电流I,若要使线圈中产生一个顺时针的电流,导线中的电流方向和大小可能是( )
 如图所示:直导线MN放置在闭合线圈上且相互绝缘,导线到圆心的距离为d.在导线中通入一个电流I,若要使线圈中产生一个顺时针的电流,导线中的电流方向和大小可能是( )
如图所示:直导线MN放置在闭合线圈上且相互绝缘,导线到圆心的距离为d.在导线中通入一个电流I,若要使线圈中产生一个顺时针的电流,导线中的电流方向和大小可能是( )| A. | 电流方向由M-N,大小逐渐减小 | B. | 电流方向由M-N,大小逐渐增加 | ||
| C. | 电流方向由N-M,大小逐渐减小 | D. | 电流方向由N-M,大小逐渐增加 |
10.如图所示,小球用轻弹簧连接,由水平位置释放(不计空气阻力),在小球摆至最低点的过程中( ) 

| A. | 小球的机械能守恒 | B. | 小球的重力势能减小 | ||
| C. | 小球的机械能减小 | D. | 小球、弹簧组成的系统机械能守恒 |
10. 如图所示,虚线所围矩形区域abcd内充满磁感应强度为B、方向垂直纸面向里的匀强磁场(矩形边线上无磁场).现从ad边的中点O处,某一粒子以大小为v的速度垂直于磁场射入、方向与ad边夹角为45°时,其轨迹恰好与ab边相切.若撤去磁场,在此矩形区域内加竖直向上的匀强电场,使该粒子仍以大小为v的速度在O处垂直于电场方向射入,恰好从b点穿出.粒子重力不计,ad边长为l,ab边长为2l,则下列说法中正确的是( )
如图所示,虚线所围矩形区域abcd内充满磁感应强度为B、方向垂直纸面向里的匀强磁场(矩形边线上无磁场).现从ad边的中点O处,某一粒子以大小为v的速度垂直于磁场射入、方向与ad边夹角为45°时,其轨迹恰好与ab边相切.若撤去磁场,在此矩形区域内加竖直向上的匀强电场,使该粒子仍以大小为v的速度在O处垂直于电场方向射入,恰好从b点穿出.粒子重力不计,ad边长为l,ab边长为2l,则下列说法中正确的是( )
 如图所示,虚线所围矩形区域abcd内充满磁感应强度为B、方向垂直纸面向里的匀强磁场(矩形边线上无磁场).现从ad边的中点O处,某一粒子以大小为v的速度垂直于磁场射入、方向与ad边夹角为45°时,其轨迹恰好与ab边相切.若撤去磁场,在此矩形区域内加竖直向上的匀强电场,使该粒子仍以大小为v的速度在O处垂直于电场方向射入,恰好从b点穿出.粒子重力不计,ad边长为l,ab边长为2l,则下列说法中正确的是( )
如图所示,虚线所围矩形区域abcd内充满磁感应强度为B、方向垂直纸面向里的匀强磁场(矩形边线上无磁场).现从ad边的中点O处,某一粒子以大小为v的速度垂直于磁场射入、方向与ad边夹角为45°时,其轨迹恰好与ab边相切.若撤去磁场,在此矩形区域内加竖直向上的匀强电场,使该粒子仍以大小为v的速度在O处垂直于电场方向射入,恰好从b点穿出.粒子重力不计,ad边长为l,ab边长为2l,则下列说法中正确的是( )| A. | 匀强磁场的磁感应强度大小与匀强电场的电场强度大小之比为$\frac{4(2+\sqrt{2})}{v}$ | |
| B. | 匀强磁场的磁感应强度大小与匀强电场的电场强度大小之比为$\frac{4(2-\sqrt{2})}{v}$ | |
| C. | 粒子穿过磁场和电场的时间之比为$\frac{5(2+\sqrt{2})π}{16}$ | |
| D. | 粒子穿过磁场和电场的时间之比为$\frac{5(2-\sqrt{2})π}{16}$ |
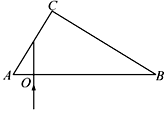
7. 如图所示,长为L的细绳一端固定于O点,另一端系一个质量为m的小球,将细绳在水平方向拉直,从静止状态释放小球,小球运动到最低点时速度大小为v,细绳拉力为F,小球的向心加速度为a,则下列说法正确的是( )
如图所示,长为L的细绳一端固定于O点,另一端系一个质量为m的小球,将细绳在水平方向拉直,从静止状态释放小球,小球运动到最低点时速度大小为v,细绳拉力为F,小球的向心加速度为a,则下列说法正确的是( )
 如图所示,长为L的细绳一端固定于O点,另一端系一个质量为m的小球,将细绳在水平方向拉直,从静止状态释放小球,小球运动到最低点时速度大小为v,细绳拉力为F,小球的向心加速度为a,则下列说法正确的是( )
如图所示,长为L的细绳一端固定于O点,另一端系一个质量为m的小球,将细绳在水平方向拉直,从静止状态释放小球,小球运动到最低点时速度大小为v,细绳拉力为F,小球的向心加速度为a,则下列说法正确的是( )| A. | 小球质量变为2m,其他条件不变,则小球到最低点的速度为v | |
| B. | 小球质量变为2m,其他条件不变,则小球到最低点时细绳拉力变为2F | |
| C. | 细绳长度变为2L,其他条件不变,小球到最低点时向心加速度变为2a | |
| D. | 细绳长度变为2L,其他条件不变,小球到最低点时向心加速度为a |
8. 如图所示,一细杆与水桶相连,水桶中装有水,水桶与细杆一起在竖直平面内做圆周运动,已知,水的质量m=0.5kg,水的重心到转轴的距离L=90cm.(取g=10m/s2,不计空气阻力)则( )
如图所示,一细杆与水桶相连,水桶中装有水,水桶与细杆一起在竖直平面内做圆周运动,已知,水的质量m=0.5kg,水的重心到转轴的距离L=90cm.(取g=10m/s2,不计空气阻力)则( )
 如图所示,一细杆与水桶相连,水桶中装有水,水桶与细杆一起在竖直平面内做圆周运动,已知,水的质量m=0.5kg,水的重心到转轴的距离L=90cm.(取g=10m/s2,不计空气阻力)则( )
如图所示,一细杆与水桶相连,水桶中装有水,水桶与细杆一起在竖直平面内做圆周运动,已知,水的质量m=0.5kg,水的重心到转轴的距离L=90cm.(取g=10m/s2,不计空气阻力)则( )| A. | 水桶不管以多大的速度通过最高点,都会有水流出 | |
| B. | 若在最高点水不流出来,桶的最小速率为3m/s | |
| C. | 若在最低点水桶的速率v=3m/s,水对桶底的压力0 | |
| D. | 若在最低点水桶的速率v=5m/s,水对桶底的压力$\frac{80}{9}$N |