题目内容
15.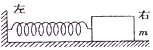 如图所示,物块的质量为m,它与水平桌面间的动摩擦因数为μ.起初,用手按住物块,物块的速度为零,弹簧的伸长量为x.然后放手,当弹簧第一次恢复原长时,物块的速度为v.则此过程中弹力所做的功为( )
如图所示,物块的质量为m,它与水平桌面间的动摩擦因数为μ.起初,用手按住物块,物块的速度为零,弹簧的伸长量为x.然后放手,当弹簧第一次恢复原长时,物块的速度为v.则此过程中弹力所做的功为( )| A. | $\frac{1}{2}$mv2+μmgx | B. | $\frac{1}{2}$mv2-μmgx | C. | μmgx-$\frac{1}{2}$mv2 | D. | 以上选项均不对 |
分析 对物体而言,除弹簧弹力外,还要克服滑动摩擦力做功,根据动能定理列式即可求解出弹簧弹力做的功.
解答 解:对物块,由动能定理得:W-μmgx=$\frac{1}{2}$mv2-0,
解得,弹簧弹力做功:W=μmgx+$\frac{1}{2}$mv2;故A正确,BCD错误.
故选:A.
点评 本题考查了动能定理的应用,要注意分析清楚物体的运动过程,明确初末状态,再应用动能定理即可正确解题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
10.如图所示,小球用轻弹簧连接,由水平位置释放(不计空气阻力),在小球摆至最低点的过程中( ) 

| A. | 小球的机械能守恒 | B. | 小球的重力势能减小 | ||
| C. | 小球的机械能减小 | D. | 小球、弹簧组成的系统机械能守恒 |
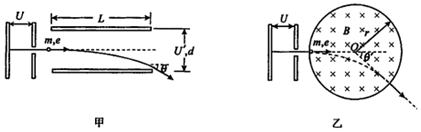
10. 如图所示,虚线所围矩形区域abcd内充满磁感应强度为B、方向垂直纸面向里的匀强磁场(矩形边线上无磁场).现从ad边的中点O处,某一粒子以大小为v的速度垂直于磁场射入、方向与ad边夹角为45°时,其轨迹恰好与ab边相切.若撤去磁场,在此矩形区域内加竖直向上的匀强电场,使该粒子仍以大小为v的速度在O处垂直于电场方向射入,恰好从b点穿出.粒子重力不计,ad边长为l,ab边长为2l,则下列说法中正确的是( )
如图所示,虚线所围矩形区域abcd内充满磁感应强度为B、方向垂直纸面向里的匀强磁场(矩形边线上无磁场).现从ad边的中点O处,某一粒子以大小为v的速度垂直于磁场射入、方向与ad边夹角为45°时,其轨迹恰好与ab边相切.若撤去磁场,在此矩形区域内加竖直向上的匀强电场,使该粒子仍以大小为v的速度在O处垂直于电场方向射入,恰好从b点穿出.粒子重力不计,ad边长为l,ab边长为2l,则下列说法中正确的是( )
 如图所示,虚线所围矩形区域abcd内充满磁感应强度为B、方向垂直纸面向里的匀强磁场(矩形边线上无磁场).现从ad边的中点O处,某一粒子以大小为v的速度垂直于磁场射入、方向与ad边夹角为45°时,其轨迹恰好与ab边相切.若撤去磁场,在此矩形区域内加竖直向上的匀强电场,使该粒子仍以大小为v的速度在O处垂直于电场方向射入,恰好从b点穿出.粒子重力不计,ad边长为l,ab边长为2l,则下列说法中正确的是( )
如图所示,虚线所围矩形区域abcd内充满磁感应强度为B、方向垂直纸面向里的匀强磁场(矩形边线上无磁场).现从ad边的中点O处,某一粒子以大小为v的速度垂直于磁场射入、方向与ad边夹角为45°时,其轨迹恰好与ab边相切.若撤去磁场,在此矩形区域内加竖直向上的匀强电场,使该粒子仍以大小为v的速度在O处垂直于电场方向射入,恰好从b点穿出.粒子重力不计,ad边长为l,ab边长为2l,则下列说法中正确的是( )| A. | 匀强磁场的磁感应强度大小与匀强电场的电场强度大小之比为$\frac{4(2+\sqrt{2})}{v}$ | |
| B. | 匀强磁场的磁感应强度大小与匀强电场的电场强度大小之比为$\frac{4(2-\sqrt{2})}{v}$ | |
| C. | 粒子穿过磁场和电场的时间之比为$\frac{5(2+\sqrt{2})π}{16}$ | |
| D. | 粒子穿过磁场和电场的时间之比为$\frac{5(2-\sqrt{2})π}{16}$ |
20. 如图所示,倒置的光滑圆锥面内侧有两个完全相同的玻璃小球 A、B 沿锥面在水平面 做匀速圆周运动,则下列关系式正确的是( )
如图所示,倒置的光滑圆锥面内侧有两个完全相同的玻璃小球 A、B 沿锥面在水平面 做匀速圆周运动,则下列关系式正确的是( )
 如图所示,倒置的光滑圆锥面内侧有两个完全相同的玻璃小球 A、B 沿锥面在水平面 做匀速圆周运动,则下列关系式正确的是( )
如图所示,倒置的光滑圆锥面内侧有两个完全相同的玻璃小球 A、B 沿锥面在水平面 做匀速圆周运动,则下列关系式正确的是( )| A. | 它们的线速度 vA>vB | B. | 它们的角速度ωA>ωB | ||
| C. | 它们的向心加速度 aA=aB | D. | 它们的向心力 FA=FB |
7. 如图所示,长为L的细绳一端固定于O点,另一端系一个质量为m的小球,将细绳在水平方向拉直,从静止状态释放小球,小球运动到最低点时速度大小为v,细绳拉力为F,小球的向心加速度为a,则下列说法正确的是( )
如图所示,长为L的细绳一端固定于O点,另一端系一个质量为m的小球,将细绳在水平方向拉直,从静止状态释放小球,小球运动到最低点时速度大小为v,细绳拉力为F,小球的向心加速度为a,则下列说法正确的是( )
 如图所示,长为L的细绳一端固定于O点,另一端系一个质量为m的小球,将细绳在水平方向拉直,从静止状态释放小球,小球运动到最低点时速度大小为v,细绳拉力为F,小球的向心加速度为a,则下列说法正确的是( )
如图所示,长为L的细绳一端固定于O点,另一端系一个质量为m的小球,将细绳在水平方向拉直,从静止状态释放小球,小球运动到最低点时速度大小为v,细绳拉力为F,小球的向心加速度为a,则下列说法正确的是( )| A. | 小球质量变为2m,其他条件不变,则小球到最低点的速度为v | |
| B. | 小球质量变为2m,其他条件不变,则小球到最低点时细绳拉力变为2F | |
| C. | 细绳长度变为2L,其他条件不变,小球到最低点时向心加速度变为2a | |
| D. | 细绳长度变为2L,其他条件不变,小球到最低点时向心加速度为a |
4. 如图所示,两个质量不同的小球用长度不等的细线拴在同一点,并在同一水平面内做匀速圆周运动,则它们的( )
如图所示,两个质量不同的小球用长度不等的细线拴在同一点,并在同一水平面内做匀速圆周运动,则它们的( )
 如图所示,两个质量不同的小球用长度不等的细线拴在同一点,并在同一水平面内做匀速圆周运动,则它们的( )
如图所示,两个质量不同的小球用长度不等的细线拴在同一点,并在同一水平面内做匀速圆周运动,则它们的( )| A. | 角速度大小相等 | B. | 线速度的大小相等 | ||
| C. | 外圈运动的小球周期大 | D. | 向心加速度的大小相等 |
5.下列说法中正确的是( )
| A. | 将一滴红墨水滴入一盆清水中,不久整盆水都变红了,这是因为分子间距离较大 | |
| B. | 做功和热传递是改变物体内能的两种方式,但本质是不同的 | |
| C. | 导热性能各向同性的固体,一定不是单晶体 | |
| D. | 自行车打气越打越困难主要是因为胎内气体压强增大而非分子间相互排斥的原因 |
 如图甲所示,一轻质弹簧上端固定在O点,下端与一质量为m=1kg的物块A连接,物块A放在水平托盘B上.开始时,A、B均处于静止且弹簧处于原长状态,现通过控制托盘B的运动使物块A以一定的加速度向下匀加速运动,运动过程中B对A的作用力F大小与弹簧伸长量x之间的关系如图乙所示,A、B恰要分离时弹簧的弹性势能为0.16J,g取10m/s2.求:
如图甲所示,一轻质弹簧上端固定在O点,下端与一质量为m=1kg的物块A连接,物块A放在水平托盘B上.开始时,A、B均处于静止且弹簧处于原长状态,现通过控制托盘B的运动使物块A以一定的加速度向下匀加速运动,运动过程中B对A的作用力F大小与弹簧伸长量x之间的关系如图乙所示,A、B恰要分离时弹簧的弹性势能为0.16J,g取10m/s2.求: