题目内容
6. 如图所示,一不可伸长的轻绳跨过两个等高的光滑定滑轮将物体a,b连在一起,质量为ma的物体a静止在倾角θ=37°的斜面体上,现将质量为mb的物体b从与滑轮等高的位置由静止释放,并摆至最低点,已知物体a在此过程中的初、末时刻均恰好处于静止状态.滑动摩擦力视为与最大静摩擦力相等,下列说法正确的是( )
如图所示,一不可伸长的轻绳跨过两个等高的光滑定滑轮将物体a,b连在一起,质量为ma的物体a静止在倾角θ=37°的斜面体上,现将质量为mb的物体b从与滑轮等高的位置由静止释放,并摆至最低点,已知物体a在此过程中的初、末时刻均恰好处于静止状态.滑动摩擦力视为与最大静摩擦力相等,下列说法正确的是( )| A. | 物体a与斜面间的动摩擦因数为0.5 | |
| B. | ma:mb=5:2 | |
| C. | 若将天花板上的滑轮水平向右移动少许,则当物体b摆过的角度为小于90°的某值时,物体a将产生滑动 | |
| D. | 若将天花板上的滑轮水平向右移动少许,则物体b摆到最低点的过程中,物体a仍静止在斜面上 |
分析 对a进行受力分析,结合共点力平衡的条件即可得出动摩擦因数;由动能定理求出b到最低点的速度,由牛顿第二定律求绳子对b的拉力,然后对a由平衡条件求出物块a所受的摩擦力.联立分析即可.
解答 解:A、开始时a恰好静止,则:μmagcos37°=magsin37°,即:$μ=tan37°=\frac{3}{4}$.故A错误;
B、b到达最低点时:$\frac{1}{2}{m}_{b}{v}^{2}={m}_{b}gR$
又:$\frac{m{v}_{b}^{2}}{R}=T-mg$
联立得:T=3mbg
a恰好平衡,则:T=μmagcos37°+magsin37°
联立得:${m}_{b}=\frac{2}{5}{m}_{a}$.故B正确;
C、D、b在向下摆动的过程中,重力与绳子的拉力的合力提供向心力,由机械能守恒可知,b的位置越靠下速度越大,需要的向心力越大,同时重力沿绳子方向的分力也越大,所以b的位置越靠下绳子的拉力越大,最大值始终等于3mbg,与滑轮的位置无关,所以,将天花板上的滑轮水平向右移动少许,则物体b摆到最低点的过程中,物体a仍静止在斜面上.故C错误,D正确.
故选:BD
点评 本题关键是先根据机械能守恒求出小球b在最低点速度,再根据向心力公式得出球对细线的拉力,最后对滑块a受力分析后根据共点力平衡条件判断静摩擦力变化情况,同时要注意研究对象的灵活选择.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
17.下列说法正确的是( )
| A. | 液体分子的无规则运动称为布朗运动 | |
| B. | 当人们感到干燥时,空气的相对湿度一定较小 | |
| C. | 温度是描述热运动的物理量,一个系统与另一个系统达到热平衡时两系统温度相同 | |
| D. | 根据热力学定律,热机的效率可以达到100% | |
| E. | 液体表面层的分子比液体内部的分子有更大的势能 |
1. 如图所示,倾斜的传送带保持静止,一木块从顶端以一定的初速度匀加速下滑到底端.如果让传送带沿图中虚线箭头所示的方向匀速运动,同样的木块从顶端以同样的初速度下滑到底端的过程中,与传送带保持静止时相比( )
如图所示,倾斜的传送带保持静止,一木块从顶端以一定的初速度匀加速下滑到底端.如果让传送带沿图中虚线箭头所示的方向匀速运动,同样的木块从顶端以同样的初速度下滑到底端的过程中,与传送带保持静止时相比( )
 如图所示,倾斜的传送带保持静止,一木块从顶端以一定的初速度匀加速下滑到底端.如果让传送带沿图中虚线箭头所示的方向匀速运动,同样的木块从顶端以同样的初速度下滑到底端的过程中,与传送带保持静止时相比( )
如图所示,倾斜的传送带保持静止,一木块从顶端以一定的初速度匀加速下滑到底端.如果让传送带沿图中虚线箭头所示的方向匀速运动,同样的木块从顶端以同样的初速度下滑到底端的过程中,与传送带保持静止时相比( )| A. | 木块从顶端滑到底端的过程中,所用的时间变长 | |
| B. | 木块从顶端滑到底端的过程中,所用的时间不变 | |
| C. | 木块在滑到底端的过程中,克服摩擦力所做的功变小 | |
| D. | 木块在滑到底端的过程中,系统产生的内能数值将变大 |
15.国际单位制中,不是电场强度的单位是( )
| A. | N/C | B. | V/m | C. | J/C | D. | T•m/s |
18.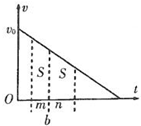 一个物体以初速度v0沿光滑斜面向上运动,其速度v随时间t变化的规律如图所示,在连续两段时间m和n内对应面积均为S,则b时刻速度vb的大小为( )
一个物体以初速度v0沿光滑斜面向上运动,其速度v随时间t变化的规律如图所示,在连续两段时间m和n内对应面积均为S,则b时刻速度vb的大小为( )
 一个物体以初速度v0沿光滑斜面向上运动,其速度v随时间t变化的规律如图所示,在连续两段时间m和n内对应面积均为S,则b时刻速度vb的大小为( )
一个物体以初速度v0沿光滑斜面向上运动,其速度v随时间t变化的规律如图所示,在连续两段时间m和n内对应面积均为S,则b时刻速度vb的大小为( )| A. | $\frac{({m}^{2}+{n}^{2})S}{(m+n)mn}$ | B. | $\frac{mn({m}^{2}+{n}^{2})S}{(m+n)}$ | C. | $\frac{(m-n)S}{mn}$ | D. | $\frac{({m}^{2}+{n}^{2})S}{mn}$ |
 如图所示,卡车通过定滑轮以恒定的功率P0拉绳,牵引河中的小船沿水面运动,已知小船的质量为m,沿水面运动时所受的阻力为f且保持不变,当绳AO段与水平面夹角为θ时,小船的速度为v,不计绳子与滑轮的摩擦,则此时绳子的拉力大小为$\frac{{P}_{0}}{vcosθ}$,小船的加速度大小为$\frac{{P}_{0}-fv}{mv}$.
如图所示,卡车通过定滑轮以恒定的功率P0拉绳,牵引河中的小船沿水面运动,已知小船的质量为m,沿水面运动时所受的阻力为f且保持不变,当绳AO段与水平面夹角为θ时,小船的速度为v,不计绳子与滑轮的摩擦,则此时绳子的拉力大小为$\frac{{P}_{0}}{vcosθ}$,小船的加速度大小为$\frac{{P}_{0}-fv}{mv}$.