题目内容
11. 某探险队员在探险时遇到一山沟,山沟两侧的高度差h=2.45m,该队员以v0=6m/s的速度沿水平方向从A点跳出,恰好落到B点(g取10m/s2),求:
某探险队员在探险时遇到一山沟,山沟两侧的高度差h=2.45m,该队员以v0=6m/s的速度沿水平方向从A点跳出,恰好落到B点(g取10m/s2),求:(1)该队员在空中运动的时间t;
(2)B点与A点间的水平距离x;
(3)该队员落到B点时的速率v(结果可保留根式).
分析 根据高度求出平抛运动的时间,根据初速度和时间求出B和A点间的水平距离.根据速度时间公式求出B点的竖直分速度,结合平行四边形定则求出B点的速率.
解答 解:(1)根据h=$\frac{1}{2}g{t}^{2}$得,t=$\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×2.45}{10}}s=0.7s$.
(2)B和A点间的水平距离x=v0t=6×0.7m=4.2m.
(3)B点的竖直分速度vy=gt=10×0.7m/s=7m/s,
则B点的速率v=$\sqrt{{{v}_{0}}^{2}+{{v}_{y}}^{2}}=\sqrt{36+49}m/s=\sqrt{85}$m/s.
答:(1)该队员在空中运动的时间为0.7s;
(2)B点与A点间的水平距离为4.2m;
(3)该队员落到B点时的速率为$\sqrt{85}$m/s.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解,基础题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
19.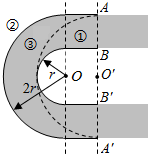 如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r,一辆质量为m的赛车通过AB线经弯道到达A′B′线,有如图所示的①、②、③三条路线,其中路线③是以O′为圆心的半圆,OO′=r,赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax,选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则( )
如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r,一辆质量为m的赛车通过AB线经弯道到达A′B′线,有如图所示的①、②、③三条路线,其中路线③是以O′为圆心的半圆,OO′=r,赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax,选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则( )
 如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r,一辆质量为m的赛车通过AB线经弯道到达A′B′线,有如图所示的①、②、③三条路线,其中路线③是以O′为圆心的半圆,OO′=r,赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax,选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则( )
如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r,一辆质量为m的赛车通过AB线经弯道到达A′B′线,有如图所示的①、②、③三条路线,其中路线③是以O′为圆心的半圆,OO′=r,赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax,选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则( )| A. | 选择路线①,赛车经过的路程最短 | |
| B. | 选择路线②,赛车的速率最小 | |
| C. | 选择路线③,赛车所用时间最短 | |
| D. | ①、②、③三条路线的圆弧上,赛车的向心加速度大小相等 |
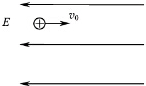
16.一带正电的小球向右水平抛入范围足够大的匀强电场,电场方向水平向左,不计空气阻力,则小球( )

| A. | 做直线运动 | B. | 做曲线运动 | ||
| C. | 速率先减小后增大 | D. | 速率先增大后减小 |
1.关于向心加速度的物理意义,下列说法中正确的是( )
| A. | 它只改变线速度的方向 | |
| B. | 它描述的是线速度大小变化的快慢 | |
| C. | 它描述的是角速度变化的快慢 | |
| D. | 匀速圆周运动的向心加速度是恒定不变的 |


