题目内容
11. 在宽度为L的条形区域内有坚直方向的匀强电场,电场的方向平行于区域边界.有一个带电粒子(不计重力)从左侧边界上的A点,以初速度v0沿垂直于电场的方向射入电场,粒子从右侧边界射出时的速度大小为$\frac{\sqrt{17}}{4}$v0.
在宽度为L的条形区域内有坚直方向的匀强电场,电场的方向平行于区域边界.有一个带电粒子(不计重力)从左侧边界上的A点,以初速度v0沿垂直于电场的方向射入电场,粒子从右侧边界射出时的速度大小为$\frac{\sqrt{17}}{4}$v0.(1)求粒子从右侧边界射出时,坚直方向的速度大小;
(2)求粒子在电场中的加速度大小及从右侧边界射出时,沿电场方向位移的大小;
(2)若带电粒子的入射速度改为$\frac{1}{4}$v0,求粒子从右侧边界射出时速度的大小.
分析 (1)粒子在电场中做类平抛运动,将运动沿水平方向与竖直方向分解即可求出;
(2)将粒子的运动分解,求出末速度的表达式,然后依据二项式定理即可求出;
(3)根据运动的合成与分解,结合运动学公式,及矢量的合成法则,即可求解.
解答 解:(1)射出电场的速度分解为水平方向和竖直方向,
则有:$\frac{\sqrt{17}}{4}{v}_{0}$=$\sqrt{{v}_{0}^{2}+{v}_{y1}^{2}}$
解得:${v_{y1}}=\frac{1}{4}{v_0}$
(2),设经过时间t1粒子射出电场,沿电场方向位移y,
由类平抛运动知
L=v0t1,vy1=at1;
得:a=$\frac{{v}_{0}^{2}}{4L}$
由y=$\frac{1}{2}a{t}_{1}^{2}$,解得:y=$\frac{L}{8}$
(3)粒子在水平方向做匀速运动,设经过时间t2;
粒子射出电场:$L=\frac{{v}_{0}{t}_{2}}{4}$
设粒子沿场强方向加速度为a,沿场强方向匀加速直线运动:vy2=at2;
粒子射出电场速度v0
v=$\sqrt{(\frac{{v}_{0}}{4})^{2}+({v}_{y2})^{2}}$
联立上式,解得:v=$\frac{\sqrt{17}}{4}{v}_{0}$
答:(1)粒子从右侧边界射出时,坚直方向的速度大小$\frac{{v}_{0}}{4}$;
(2)粒子在电场中的加速度大小及从右侧边界射出时,沿电场方向位移的大小$\frac{L}{8}$;
(2)若带电粒子的入射速度改为$\frac{1}{4}$v0,粒子从右侧边界射出时速度的大小$\frac{\sqrt{17}}{4}{v}_{0}$.
点评 该题考查带电粒子在电场中的偏转,解答的难点是第二位,要正确写出粒子的末速度的表达式,才能正确得出结论.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案 水平平行放置的金属板a、b间加上恒定电压,两板间距离为d.一带电粒子紧贴a板水平射入电场,刚好紧贴b板射出,如图所示.在其他条件不变的情况下,若将b板向下平移一段距离x,带电粒子刚好从两板中央射出.不考虑重力的影响,则( )
水平平行放置的金属板a、b间加上恒定电压,两板间距离为d.一带电粒子紧贴a板水平射入电场,刚好紧贴b板射出,如图所示.在其他条件不变的情况下,若将b板向下平移一段距离x,带电粒子刚好从两板中央射出.不考虑重力的影响,则( )| A. | x=d | B. | x=$\frac{1}{2}$d | C. | x=$\sqrt{2}$d | D. | x=($\sqrt{2}-1$)d |
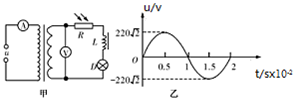 如图甲所示的电路中,理想变压器原、副线圈匝数比为10:1,A、V均为理想电表,R、L和D分别是光敏电阻(其阻值随光强增大而减小)、理想线圈和灯泡.原线圈接入如图乙所示的正弦交流电压u,下列说法正确的是( )
如图甲所示的电路中,理想变压器原、副线圈匝数比为10:1,A、V均为理想电表,R、L和D分别是光敏电阻(其阻值随光强增大而减小)、理想线圈和灯泡.原线圈接入如图乙所示的正弦交流电压u,下列说法正确的是( )| A. | 电压u的频率为100 Hz | B. | V的示数为22$\sqrt{2}$V | ||
| C. | 有光照射R时,A的示数变大 | D. | 抽出L中的铁芯,D变暗 |
 如图所示,静止在斜面上的气缸内用质量为m的活塞封闭一段气体,给气缸一个沿斜面向上的初速度,则在向上滑行的过程中缸内气体与气缸静止在斜面上时相比( )
如图所示,静止在斜面上的气缸内用质量为m的活塞封闭一段气体,给气缸一个沿斜面向上的初速度,则在向上滑行的过程中缸内气体与气缸静止在斜面上时相比( )| A. | 压强增大,体积增大 | B. | 压强增大,体积減小 | ||
| C. | 压强減小,体积增大 | D. | 压强减小,体积減小 |
 如图所示,匀强磁场的磁感应强度大小为B.匝数为N、面积为S的矩形线圈绕垂直于磁场的轴OO′以角速度ω匀速转动,不计线圈电阻.线圈通过电刷与一理想变压器原线圈相接,变压器的原、副线圈的匝数分别为n1、n2.A为理想交流电流表.L1、L2为两个完全相同的电灯泡,标称值为“U0,P0”,且当S闭合时两灯泡均正常发光.除灯泡电阻外,不计其它电阻.则以下说法正确的是( )
如图所示,匀强磁场的磁感应强度大小为B.匝数为N、面积为S的矩形线圈绕垂直于磁场的轴OO′以角速度ω匀速转动,不计线圈电阻.线圈通过电刷与一理想变压器原线圈相接,变压器的原、副线圈的匝数分别为n1、n2.A为理想交流电流表.L1、L2为两个完全相同的电灯泡,标称值为“U0,P0”,且当S闭合时两灯泡均正常发光.除灯泡电阻外,不计其它电阻.则以下说法正确的是( )| A. | 从图示位置开始计时,线框内产生的交变电流的电动势随时间的瞬时值表达式为e=NBSωcosωt | |
| B. | 理想变压器原副线圈的匝数比为$\frac{{n}_{1}}{{n}_{2}}$=$\frac{NBSω}{\sqrt{2}{U}_{0}}$ | |
| C. | 当S断开后,L1比断开前暗 | |
| D. | 当S断开后,电流表的示数比断开前大 |
 如图所示,理想变压器的原、副线圈匝数之比为n1:n2=4:1,原线圈回路中与副线圈回路中各接有电阻A、B.a、b端加一交流电压U后,两电阻消耗的电功率相同,则( )
如图所示,理想变压器的原、副线圈匝数之比为n1:n2=4:1,原线圈回路中与副线圈回路中各接有电阻A、B.a、b端加一交流电压U后,两电阻消耗的电功率相同,则( )| A. | A、B电阻之比为8:1 | B. | A、B电阻之比为16:1 | ||
| C. | 变压器的输入电压为$\frac{U}{2}$ | D. | 变压器的输出电压为$\frac{U}{2}$ |

