题目内容
3.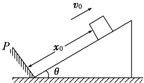 如图所示,斜面的倾角为θ,质量为m的滑块距挡板P的距离为x0,滑块以初速度v0沿斜面上滑,滑块与斜面间的动摩擦因数为μ,滑块所受摩擦力小于重力沿斜面向下的分力.若滑块每次与挡板相碰均无机械能损失,滑块经过的总路程是( )
如图所示,斜面的倾角为θ,质量为m的滑块距挡板P的距离为x0,滑块以初速度v0沿斜面上滑,滑块与斜面间的动摩擦因数为μ,滑块所受摩擦力小于重力沿斜面向下的分力.若滑块每次与挡板相碰均无机械能损失,滑块经过的总路程是( )| A. | $\frac{1}{μ}$($\frac{{{v}_{0}}^{2}}{2gcosθ}$+x0tanθ) | B. | $\frac{1}{μ}$($\frac{{{v}_{0}}^{2}}{2gsinθ}$+x0tanθ) | ||
| C. | $\frac{2}{μ}$($\frac{{{v}_{0}}^{2}}{2gcosθ}$+x0tanθ) | D. | $\frac{1}{μ}$($\frac{{{v}_{0}}^{2}}{2gcosθ}$+x0cotθ) |
分析 题中滑块所受摩擦力小于重力沿斜面向下的分力,滑块与挡板碰撞后向上运动的过程中,不能停在最高点,又向下滑动,滑块的机械能不断减小,最终滑块停在斜面底部.滑块摩擦生热与总路程成正比Q=fs,s是总路程.在整个运动过程中滑块和挡板的碰撞没有能量损失,重力势能和动能减小转化为摩擦产生的内能,根据能量守恒求解.
解答 解:由题分析可知,滑块最终停在斜面底部,设滑块经过的总路程为s.
根据能量守恒定律,滑块的机械能全部转化为内能,则有
μmgscosθ=$\frac{1}{2}$m${v}_{0}^{2}$+mgx0sinθ
解得:s=$\frac{1}{μ}$($\frac{{{v}_{0}}^{2}}{2gcosθ}$+x0tanθ)
故选:A.
点评 本题首先要通过分析判断出滑块最终停在斜面的底部;二要抓住滑动摩擦力做功与总路程有关,也可以应用动能定理求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列说法中正确的是( )
| A. | 曲线运动一定是变速运动 | |
| B. | 变速运动一定是曲线运动 | |
| C. | 匀速圆周运动就是速度不变的运动 | |
| D. | 匀速圆周运动就是角速度不变的运动 |
11. 质量为m的小球,从离桌面H高处由静止开始落下,桌面离地面高度为h,如图所示.若以桌面作为重力势能等于零的参考平面,那么当小球落地时的动能为(不计空气阻力)( )
质量为m的小球,从离桌面H高处由静止开始落下,桌面离地面高度为h,如图所示.若以桌面作为重力势能等于零的参考平面,那么当小球落地时的动能为(不计空气阻力)( )
 质量为m的小球,从离桌面H高处由静止开始落下,桌面离地面高度为h,如图所示.若以桌面作为重力势能等于零的参考平面,那么当小球落地时的动能为(不计空气阻力)( )
质量为m的小球,从离桌面H高处由静止开始落下,桌面离地面高度为h,如图所示.若以桌面作为重力势能等于零的参考平面,那么当小球落地时的动能为(不计空气阻力)( )| A. | mhH | B. | mgh | C. | mg(H+h) | D. | mg(H-h) |
15.在如图所示的电路中,A1和A2是完全相同的灯泡,线圈L的电阻可忽略,下列说法中正确的是( ) 

| A. | 合上开关K接通电路时,A2先亮,A1后亮,最后一样亮 | |
| B. | 合上开关K接通电路时,A1和A2始终一样亮 | |
| C. | 断开开关K切断电路时,A1和A2都立即熄灭 | |
| D. | 断开开关K切断电路时,A2立即熄灭,A1过一会儿才熄灭 |
 长为2m的细线,其最大承受拉力为20N,在线的中点位置O点系一质量为2kg的小球(可视为质点),线的一端固定在一水平滑杆的A点(滑杆足够长),线的另一端系一小环B,B恰能套在滑杆上,初始时,两线处在竖直位置,如图所示,现缓慢地用力沿滑杆向右拉B环,使小球缓慢上升,设线的长度不变,g取10m/s2,求:
长为2m的细线,其最大承受拉力为20N,在线的中点位置O点系一质量为2kg的小球(可视为质点),线的一端固定在一水平滑杆的A点(滑杆足够长),线的另一端系一小环B,B恰能套在滑杆上,初始时,两线处在竖直位置,如图所示,现缓慢地用力沿滑杆向右拉B环,使小球缓慢上升,设线的长度不变,g取10m/s2,求: 如图所示,在粗糙水平台阶上静止放置一质量m=0.5kg的小物块,它与水平台阶表面的动摩擦因数μ=0.5,且与台阶边缘O点的距离s=5m.在台阶右侧固定了一个$\frac{1}{4}$圆弧挡板,圆弧半径R=1m,圆弧的圆心也在O点.今以O点为原点建立平面直角坐标系.现用F=5N的水平恒力拉动小物块,一段时间后撤去拉力,小物块最终水平抛出并击中挡板.(g取10m/s2)
如图所示,在粗糙水平台阶上静止放置一质量m=0.5kg的小物块,它与水平台阶表面的动摩擦因数μ=0.5,且与台阶边缘O点的距离s=5m.在台阶右侧固定了一个$\frac{1}{4}$圆弧挡板,圆弧半径R=1m,圆弧的圆心也在O点.今以O点为原点建立平面直角坐标系.现用F=5N的水平恒力拉动小物块,一段时间后撤去拉力,小物块最终水平抛出并击中挡板.(g取10m/s2) 如图所示,用某种透光物制成的直角三棱镜ABC;在垂直于AC面的直线MN上插两枚大头针P1、P2,在AB面的左侧透过棱镜观察大头针P1、P2的像,调整视线方向,直到P2的像被P1的像挡住,再在观察的这一侧先后插上两枚大头针P3、P4,使P3挡住P1、P2的像,P4挡住P1、P2的像,P4挡住P3及P1、P2的像.记下P3、P4的位置,移去大头针和三棱镜,过P3、P4的位置作直线与AB面相交于D,量出该直线与AB面的夹角为45°.则该透光物质的折射率n=1.41,并在图中画出正确完整的光路图.
如图所示,用某种透光物制成的直角三棱镜ABC;在垂直于AC面的直线MN上插两枚大头针P1、P2,在AB面的左侧透过棱镜观察大头针P1、P2的像,调整视线方向,直到P2的像被P1的像挡住,再在观察的这一侧先后插上两枚大头针P3、P4,使P3挡住P1、P2的像,P4挡住P1、P2的像,P4挡住P3及P1、P2的像.记下P3、P4的位置,移去大头针和三棱镜,过P3、P4的位置作直线与AB面相交于D,量出该直线与AB面的夹角为45°.则该透光物质的折射率n=1.41,并在图中画出正确完整的光路图. 如图所示,L1和L2是输电线,1是电压互感器,2是电流互感器.在图中空圈内填入所用的电表的符号,若已知变压比为100﹕1,变流比为1000﹕1,并且知道伏特表示数为220V,安培表示数为100A,则输电线路中的功率为2.2×109W.
如图所示,L1和L2是输电线,1是电压互感器,2是电流互感器.在图中空圈内填入所用的电表的符号,若已知变压比为100﹕1,变流比为1000﹕1,并且知道伏特表示数为220V,安培表示数为100A,则输电线路中的功率为2.2×109W.