题目内容
18. 长为2m的细线,其最大承受拉力为20N,在线的中点位置O点系一质量为2kg的小球(可视为质点),线的一端固定在一水平滑杆的A点(滑杆足够长),线的另一端系一小环B,B恰能套在滑杆上,初始时,两线处在竖直位置,如图所示,现缓慢地用力沿滑杆向右拉B环,使小球缓慢上升,设线的长度不变,g取10m/s2,求:
长为2m的细线,其最大承受拉力为20N,在线的中点位置O点系一质量为2kg的小球(可视为质点),线的一端固定在一水平滑杆的A点(滑杆足够长),线的另一端系一小环B,B恰能套在滑杆上,初始时,两线处在竖直位置,如图所示,现缓慢地用力沿滑杆向右拉B环,使小球缓慢上升,设线的长度不变,g取10m/s2,求:(1)当拉至OA于滑杆成60°角时,两线的拉力分别为多大.
(2)当拉至线刚好被拉断前位置,B环离A点的距离.
分析 (1)当拉至OA与滑杆成60°角时,以球为研究对象,根据平衡条件求解两线的拉力.
(2)当线刚好被拉断时拉力达到最大值,以球为研究对象,由平衡条件求出此时线与竖直方向的夹角,再由数学知识求解B环离A点的距离.
解答 解:(1)当拉至OA与滑杆成60°角时,OA与OB的夹角为60°,设两线的拉力均为T.
以球为研究对象,由平衡条件得:2Tcos30°=mg
可得:T=$\frac{\sqrt{3}}{3}$mg=$\frac{\sqrt{3}}{3}$×20N=$\frac{20\sqrt{3}}{3}$N
(2)设线刚好被拉断时两线OA、OB与竖直方向的夹角为α,则:
2Tmcosα=mg
得:cosα=$\frac{mg}{2{T}_{m}}$=$\frac{20}{2×20}$=$\frac{1}{2}$,α=60°
根据几何知识知,B环离A点的距离为:S=2×$\frac{1}{2}$lsinα=2×sin60° m=$\sqrt{3}$m
答:(1)当拉至OA与滑杆成60°角时,两线的拉力分别为$\frac{20\sqrt{3}}{3}$N.
(2)当拉至线刚好被拉断前位置,B环离A点的距离为$\sqrt{3}$m.
点评 本题是共点力平衡问题,关键要抓住两线关于竖直方向对称,充分运用几何知识求解相关距离.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
6.下列关于匀速圆周运动的说法中,正确的是( )
| A. | 速度不变 | B. | 速率不变 | ||
| C. | 加速度为零 | D. | 实质就是匀速运动 |
13. 蜡块能在玻璃管的水中匀速上升,若红蜡块在A点匀速上升的同时,使玻璃管水平向右做匀速直线运动,则红蜡块实际运动的轨迹是图中的( )
蜡块能在玻璃管的水中匀速上升,若红蜡块在A点匀速上升的同时,使玻璃管水平向右做匀速直线运动,则红蜡块实际运动的轨迹是图中的( )
 蜡块能在玻璃管的水中匀速上升,若红蜡块在A点匀速上升的同时,使玻璃管水平向右做匀速直线运动,则红蜡块实际运动的轨迹是图中的( )
蜡块能在玻璃管的水中匀速上升,若红蜡块在A点匀速上升的同时,使玻璃管水平向右做匀速直线运动,则红蜡块实际运动的轨迹是图中的( )| A. | 曲线Q | B. | 曲线R | C. | 直线P | D. | 无法确定 |
3.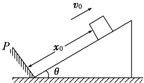 如图所示,斜面的倾角为θ,质量为m的滑块距挡板P的距离为x0,滑块以初速度v0沿斜面上滑,滑块与斜面间的动摩擦因数为μ,滑块所受摩擦力小于重力沿斜面向下的分力.若滑块每次与挡板相碰均无机械能损失,滑块经过的总路程是( )
如图所示,斜面的倾角为θ,质量为m的滑块距挡板P的距离为x0,滑块以初速度v0沿斜面上滑,滑块与斜面间的动摩擦因数为μ,滑块所受摩擦力小于重力沿斜面向下的分力.若滑块每次与挡板相碰均无机械能损失,滑块经过的总路程是( )
 如图所示,斜面的倾角为θ,质量为m的滑块距挡板P的距离为x0,滑块以初速度v0沿斜面上滑,滑块与斜面间的动摩擦因数为μ,滑块所受摩擦力小于重力沿斜面向下的分力.若滑块每次与挡板相碰均无机械能损失,滑块经过的总路程是( )
如图所示,斜面的倾角为θ,质量为m的滑块距挡板P的距离为x0,滑块以初速度v0沿斜面上滑,滑块与斜面间的动摩擦因数为μ,滑块所受摩擦力小于重力沿斜面向下的分力.若滑块每次与挡板相碰均无机械能损失,滑块经过的总路程是( )| A. | $\frac{1}{μ}$($\frac{{{v}_{0}}^{2}}{2gcosθ}$+x0tanθ) | B. | $\frac{1}{μ}$($\frac{{{v}_{0}}^{2}}{2gsinθ}$+x0tanθ) | ||
| C. | $\frac{2}{μ}$($\frac{{{v}_{0}}^{2}}{2gcosθ}$+x0tanθ) | D. | $\frac{1}{μ}$($\frac{{{v}_{0}}^{2}}{2gcosθ}$+x0cotθ) |
10.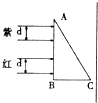 如图所示,截面为ABC的玻璃直角三棱镜放置在空气中,宽度均为d的紫、红两束光垂直照射三棱镜的一个直角边AB,在三棱镜的另一侧放置一平行于AB边的光屏,屏的距离远近可调,在屏上出现紫、红两条光带,可能是( )
如图所示,截面为ABC的玻璃直角三棱镜放置在空气中,宽度均为d的紫、红两束光垂直照射三棱镜的一个直角边AB,在三棱镜的另一侧放置一平行于AB边的光屏,屏的距离远近可调,在屏上出现紫、红两条光带,可能是( )
 如图所示,截面为ABC的玻璃直角三棱镜放置在空气中,宽度均为d的紫、红两束光垂直照射三棱镜的一个直角边AB,在三棱镜的另一侧放置一平行于AB边的光屏,屏的距离远近可调,在屏上出现紫、红两条光带,可能是( )
如图所示,截面为ABC的玻璃直角三棱镜放置在空气中,宽度均为d的紫、红两束光垂直照射三棱镜的一个直角边AB,在三棱镜的另一侧放置一平行于AB边的光屏,屏的距离远近可调,在屏上出现紫、红两条光带,可能是( )| A. | 紫色光带在上,红色光带在下,紫色光带较宽 | |
| B. | 紫色光带在下,红色光带在上,紫色光带较宽 | |
| C. | 红色光带在上,紫色光带在下,红色光带较宽 | |
| D. | 红色光带在下,紫色光带在上,紫色光带较宽 |

 如图所示,物体在与水平方向成53°的10N的力F作用下从静止开始运动,水平地面光滑,在2s内力F对物体的冲量为20N.s,2s末物体的动量为12kg.m/s.
如图所示,物体在与水平方向成53°的10N的力F作用下从静止开始运动,水平地面光滑,在2s内力F对物体的冲量为20N.s,2s末物体的动量为12kg.m/s.