题目内容
9.从离地500m的空中由静止开始自由落下一个小球,求:(1)经过多长时间小球落到地面;
(2)小球落地前最后1s内的位移.
分析 (1)根据h=$\frac{1}{2}$gt2即可求得时间;
(2)小球在落地前1s内的位移等于总位移减去(t-1)s内的位移.
解答 解:(1)由自由落体运动位移公式h=$\frac{1}{2}$gt2,
得落地时间t=$\sqrt{\frac{2×500}{10}}$s=10 s.
(2)从开始下落,前9 s内的位移为:
h9=$\frac{1}{2}$gt92=$\frac{1}{2}$×10×92 m=405 m.
小球落地前最后1 s内的位移500m-405m=95m.
答:(1)经过10s时间小球落到地面;
(2)小球落地前最后1s内的位移为95s.
点评 本题主要考查了自由落体运动基本公式的直接应用,将已知的数据代入公式即可,难度不大,属于基础题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
19. 如图所示,在半径为R的圆形区域内存在方向垂直纸面向里的匀强磁场,O为圆心,ab为直径,c为圆上一点,∠aOc=60°.甲、乙两带电粒子以相同的速率分别从a、b两端点沿半径方向射向O点,两粒子都能从c点离开磁场,不计粒子重力,则( )
如图所示,在半径为R的圆形区域内存在方向垂直纸面向里的匀强磁场,O为圆心,ab为直径,c为圆上一点,∠aOc=60°.甲、乙两带电粒子以相同的速率分别从a、b两端点沿半径方向射向O点,两粒子都能从c点离开磁场,不计粒子重力,则( )
 如图所示,在半径为R的圆形区域内存在方向垂直纸面向里的匀强磁场,O为圆心,ab为直径,c为圆上一点,∠aOc=60°.甲、乙两带电粒子以相同的速率分别从a、b两端点沿半径方向射向O点,两粒子都能从c点离开磁场,不计粒子重力,则( )
如图所示,在半径为R的圆形区域内存在方向垂直纸面向里的匀强磁场,O为圆心,ab为直径,c为圆上一点,∠aOc=60°.甲、乙两带电粒子以相同的速率分别从a、b两端点沿半径方向射向O点,两粒子都能从c点离开磁场,不计粒子重力,则( )| A. | 甲粒子带正电、乙粒子带负电 | |
| B. | 甲、乙两粒子的比荷之比为3:1 | |
| C. | 甲、乙两粒子的比荷之比为2:1 | |
| D. | 甲、乙两粒子离开磁场时的速度方向不同 |
20. 如图所示,长为L,倾角为θ的光滑绝缘斜面处于电场中,一带电量为+q,质量为m的小球,以初速度v0由斜面底端的A点开始沿斜面上滑,到达斜面顶端的速度仍为v0,则( )
如图所示,长为L,倾角为θ的光滑绝缘斜面处于电场中,一带电量为+q,质量为m的小球,以初速度v0由斜面底端的A点开始沿斜面上滑,到达斜面顶端的速度仍为v0,则( )
 如图所示,长为L,倾角为θ的光滑绝缘斜面处于电场中,一带电量为+q,质量为m的小球,以初速度v0由斜面底端的A点开始沿斜面上滑,到达斜面顶端的速度仍为v0,则( )
如图所示,长为L,倾角为θ的光滑绝缘斜面处于电场中,一带电量为+q,质量为m的小球,以初速度v0由斜面底端的A点开始沿斜面上滑,到达斜面顶端的速度仍为v0,则( )| A. | A、B两点的电势差一定为$\frac{mgLsinθ}{q}$ | |
| B. | 小球在B点的电势能一定小于小球在A点的电势能 | |
| C. | 若电场是匀强电场,则该电场的场强的最大值一定是$\frac{mg}{q}$ | |
| D. | 若该电场是斜面中点正上方某点的点电荷Q产生的,则Q一定是正电荷 |
14. 电动势为 E、内阻为 r 的电源与定值电阻 R1、R2及滑动变阻器 R 连接成电路,如图所示.当滑动变阻器的触头由中点滑向 b 端时,下列说法正确的是( )
电动势为 E、内阻为 r 的电源与定值电阻 R1、R2及滑动变阻器 R 连接成电路,如图所示.当滑动变阻器的触头由中点滑向 b 端时,下列说法正确的是( )
 电动势为 E、内阻为 r 的电源与定值电阻 R1、R2及滑动变阻器 R 连接成电路,如图所示.当滑动变阻器的触头由中点滑向 b 端时,下列说法正确的是( )
电动势为 E、内阻为 r 的电源与定值电阻 R1、R2及滑动变阻器 R 连接成电路,如图所示.当滑动变阻器的触头由中点滑向 b 端时,下列说法正确的是( )| A. | 电压表读数增大,电流表读数减小 | B. | 电压表读数减小,电流表读数减小 | ||
| C. | 滑动变阻器两端电压增大 | D. | 滑动变阻器两端电压减小 |
19.某质点的位移随时间的变化规律的关系是:x=2t+2t2,x与t的单位分别为m和s,则质点的初速度与加速度分别为( )
| A. | 2 m/s与4m/s2 | B. | 4 m/s与2 m/s2 | C. | 0与4 m/s2 | D. | 4 m/s与0 |
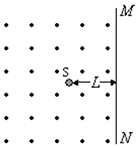 如图所示,粒子源S能在图示纸面内的360°范围内发射速率相同、质量为m、电量为+q的同种粒子(重力不计),MN是足够大的竖直挡板,S到板的距离为L,挡板左侧充满垂直纸面向外的匀强磁场,磁感应强度为B,求:
如图所示,粒子源S能在图示纸面内的360°范围内发射速率相同、质量为m、电量为+q的同种粒子(重力不计),MN是足够大的竖直挡板,S到板的距离为L,挡板左侧充满垂直纸面向外的匀强磁场,磁感应强度为B,求:
 如图所示,在长为2L、宽为L的矩形区域ABCD 内有电场强度大小为 E、方向竖直向下的匀强电场.一质量为m,电量为q的带负电的质点,以平行于 AD 的初速度从 A 点射入该区域,结果该质点恰能从 C 点射出.(已知重力加速度为 g)
如图所示,在长为2L、宽为L的矩形区域ABCD 内有电场强度大小为 E、方向竖直向下的匀强电场.一质量为m,电量为q的带负电的质点,以平行于 AD 的初速度从 A 点射入该区域,结果该质点恰能从 C 点射出.(已知重力加速度为 g)