题目内容
4. 如图所示,光滑斜面AE被分成四个相等的部分,一物体由A点从静止释放,做匀加速直线运动.下列结论正确的是( )
如图所示,光滑斜面AE被分成四个相等的部分,一物体由A点从静止释放,做匀加速直线运动.下列结论正确的是( )| A. | 物体到达各点的速率vB:vC:vD:vE=1:$\sqrt{2}$:$\sqrt{3}$:2 | |
| B. | 物体到达各点所经历的时间:tE=2tB=$\sqrt{2}$tC=$\frac{2}{\sqrt{3}}$tD | |
| C. | 物体通过每一部分时,其速度增量vB-vA=vC-vB=vD-vC=vE-vD | |
| D. | 物体从A到E的平均速度$\overline{v}$=vB |
分析 本题是同一个匀加速直线运动中不同位置的速度、时间等物理量的比较,根据选项中需要比较的物理量选择正确的公式把物理量表示出来,再进行比较.
解答 解:A、根据运动学公式${v}_{\;}^{2}-{v}_{0}^{2}=2ax$,物体由A点从静止释放${v}_{0}^{\;}=0$,所以有${v}_{\;}^{2}=2ax$
所以物体到达各点的速率之比${v}_{B}^{\;}:{v}_{C}^{\;}:{v}_{D}^{\;}:{v}_{E}^{\;}=1:\sqrt{2}:\sqrt{3}:2$,故A正确;
B、根据运动学公式$x={v}_{0}^{\;}t+\frac{1}{2}a{t}_{\;}^{2}$得:$t=\sqrt{\frac{2x}{a}}$
物体到达各点经历的时间${t}_{B}^{\;}:{t}_{C}^{\;}:{t}_{D}^{\;}:{t}_{E}^{\;}=1:\sqrt{2}:\sqrt{3}:2$
则物体到达各点所经历的时间:tE=2tB=$\sqrt{2}$tC=$\frac{2}{\sqrt{3}}$${t}_{D}^{\;}$,故B正确;
C、vB:vC:vD:vE=$1:\sqrt{2}:\sqrt{3}:2$,物体通过每一部分时其速度增量不等,故C错误
D、由于${v}_{E}^{\;}=2{v}_{B}^{\;}$,物体从A到E的平均速度$\overline{v}=\frac{0+{v}_{E}^{\;}}{2}={v}_{B}^{\;}$,故D正确;
故选:ABD
点评 本题对运动学公式要求较高,要求学生对所有的运动学公式不仅要熟悉而且要熟练,要灵活,基本方法就是平时多练并且尽可能尝试一题多解.

练习册系列答案
相关题目
15.一物体做匀加速直线运动,从某时刻开始计时,第1s内位移为1m,第2s内位移为2m…第ns内位移为n m,则( )
| A. | 物体在计时开始时刻的速度为零 | B. | 物体在2s末的速度为2.5m/s | ||
| C. | 物体的加速度大小为2m/s2 | D. | 物体在前4s内的平均速度为2m/s |
12.一辆农用“小四轮”漏油,一位同学根据漏在路面上的油滴分布,分析“小四轮”的运动情况(已知车的运动方向),假如每隔l s漏下一滴,车在平直公路上行驶,下列说法正确的是( )
| A. | 当沿运动方向油滴始终均匀分布时,车一定做匀速直线运动 | |
| B. | 当沿运动方向油滴间距逐渐增大时,车一定在做匀加速直线运动 | |
| C. | 当沿运动方向油滴间距逐渐增大时,车的加速度可能在减小 | |
| D. | 当沿运动方向油滴间距逐渐增大时,车的加速度一定在增大 |
16.关于速度和加速度的关系,下列说法正确的是( )
| A. | 加速度变大,说明速度一定变大 | |
| B. | 速度越来越大,加速度不可能越来越小 | |
| C. | 只要加速度不为零,速度一定变化 | |
| D. | 某一段时间内的加速度与速度变化毫无关系 |
13. 2016年9月15日22时04分,我国在酒泉卫星发射中心用长征二号FT2运载火箭将天宫二号空间实验室发射升空.已知天宫二号在驶向既定轨道Ⅰ过程中,在A点从椭圆形轨道Ⅱ进入圆形轨道Ⅰ,B为轨道Ⅱ上的一点,且离地球表面距离相对很小,如图所示,关于天宫二号的运动,下列说法中正确的是( )
2016年9月15日22时04分,我国在酒泉卫星发射中心用长征二号FT2运载火箭将天宫二号空间实验室发射升空.已知天宫二号在驶向既定轨道Ⅰ过程中,在A点从椭圆形轨道Ⅱ进入圆形轨道Ⅰ,B为轨道Ⅱ上的一点,且离地球表面距离相对很小,如图所示,关于天宫二号的运动,下列说法中正确的是( )
 2016年9月15日22时04分,我国在酒泉卫星发射中心用长征二号FT2运载火箭将天宫二号空间实验室发射升空.已知天宫二号在驶向既定轨道Ⅰ过程中,在A点从椭圆形轨道Ⅱ进入圆形轨道Ⅰ,B为轨道Ⅱ上的一点,且离地球表面距离相对很小,如图所示,关于天宫二号的运动,下列说法中正确的是( )
2016年9月15日22时04分,我国在酒泉卫星发射中心用长征二号FT2运载火箭将天宫二号空间实验室发射升空.已知天宫二号在驶向既定轨道Ⅰ过程中,在A点从椭圆形轨道Ⅱ进入圆形轨道Ⅰ,B为轨道Ⅱ上的一点,且离地球表面距离相对很小,如图所示,关于天宫二号的运动,下列说法中正确的是( )| A. | 在轨道Ⅱ上经过A时,天宫二号需要减速才可进入轨道Ⅰ | |
| B. | 在轨道Ⅱ上运行周期小于轨道Ⅰ上运行周期 | |
| C. | 在轨道Ⅱ上,经过A的加速度小于经过B的加速度 | |
| D. | 在B点时,航天飞机的速度大于7.9km/s |
14.关于位移和路程的说法,正确的是( )
| A. | 位移是标量,路程是矢量 | |
| B. | 在直线运动中,位移的大小和路程一定相同 | |
| C. | 在曲线运动中,位移的大小和路程可能相同 | |
| D. | 位移方向总是与质点平均速度方向一致 |
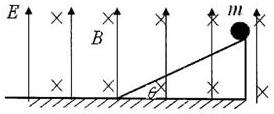 如图所示,空间内存在垂直纸面向里的匀强磁场和竖直向上的匀强电场,一带电小球(可视为质点)质量m=0.4kg,电荷量q=-0.8C,从倾角θ=37°的光滑斜面最高点由静止开始下滑,当沿斜面下滑距离s=$\frac{8}{3}$m时与斜面脱离.此时立即将电场反向,小球做匀速圆周运动,最终恰好不与地面发生碰撞,重力加速度g=10m/s2.求:
如图所示,空间内存在垂直纸面向里的匀强磁场和竖直向上的匀强电场,一带电小球(可视为质点)质量m=0.4kg,电荷量q=-0.8C,从倾角θ=37°的光滑斜面最高点由静止开始下滑,当沿斜面下滑距离s=$\frac{8}{3}$m时与斜面脱离.此时立即将电场反向,小球做匀速圆周运动,最终恰好不与地面发生碰撞,重力加速度g=10m/s2.求: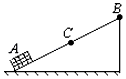 如图所示,物体(可看成质点)以4m/s的初速度自斜面底端A点滑上光滑斜面作匀减速直线运动,途经斜面中点C,到达最高点B.已知在A、C点速度vA:vC=4:3,从C点到B点历时(3-$\sqrt{2}$)s,试求:
如图所示,物体(可看成质点)以4m/s的初速度自斜面底端A点滑上光滑斜面作匀减速直线运动,途经斜面中点C,到达最高点B.已知在A、C点速度vA:vC=4:3,从C点到B点历时(3-$\sqrt{2}$)s,试求: