题目内容
2.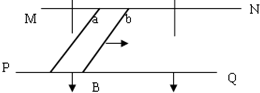 如图所示,足够长的相距为L的平行金属导轨MN、PQ放置在水平面内,匀强磁场竖直向下覆盖轨道平面,磁感应强度为B,在轨道上平行横放两根相距S0的金属导体棒a、b,使之与导轨构成矩形回路,每根金属棒的质量均为m,电阻均为R,导轨电阻可忽略,棒与导轨无摩擦,且不计重力和电磁辐射.开始时,导体棒a静止,导体棒b具有向右的初速度v0,最终两根金属棒会保持相对静止,求此时a、b棒之间的距离.
如图所示,足够长的相距为L的平行金属导轨MN、PQ放置在水平面内,匀强磁场竖直向下覆盖轨道平面,磁感应强度为B,在轨道上平行横放两根相距S0的金属导体棒a、b,使之与导轨构成矩形回路,每根金属棒的质量均为m,电阻均为R,导轨电阻可忽略,棒与导轨无摩擦,且不计重力和电磁辐射.开始时,导体棒a静止,导体棒b具有向右的初速度v0,最终两根金属棒会保持相对静止,求此时a、b棒之间的距离.
分析 两金属棒相对静止时,它们的速度相等,应用动量守恒定律求出它们的速度,由动量定理求出通过金属棒的电荷量,然后由法拉第电磁感应定律、欧姆定律、电流定义式求出a、b间的距离.
解答 解:开始b向右做减速运动,a向右做加速运动,a、b相对静止时,它们的速度相等,
a、b两金属棒组成的系统动量守恒,以b的初速度方向为正方向,
由动量守恒定律得:mv0=(m+m)v,解得:v=$\frac{1}{2}$v0,
对a,由动量定理得:BIL•t=mv-0,则:BL•It=mv-0,
BLq=mv,解得,通过金属棒的电荷量:q=$\frac{m{v}_{0}}{2BL}$,
由法拉第电磁感应定律得:$\overline{E}$=$\frac{△Φ}{△t}$=$\frac{B△S}{△t}$=$\frac{BL({S}_{0}-d)}{△t}$,
感应电流:$\overline{I}$=$\frac{\overline{E}}{2R}$,
通过金属棒的电荷量:q=$\overline{I}$△t,
则:$\frac{m{v}_{0}}{2BL}$=$\frac{BL({S}_{0}-d)}{2R}$,
解得,a、b棒之间的距离:d=S0-$\frac{m{v}_{0}R}{{B}^{2}{L}^{2}}$;
答:此时a、b棒之间的距离为:S0-$\frac{m{v}_{0}R}{{B}^{2}{L}^{2}}$.
点评 本题考查了求两金属棒间的距离,分析清楚金属棒的运动过程,应用动量守恒定律、动量定理、法拉第电磁感应定律、欧姆定律与电流定义式即可正确解题.

练习册系列答案
相关题目
13.飞船进入正常轨道后,因特殊情况而降低了轨道高度,那么飞船的线速度和周期分别将( )
| A. | 增大、减小 | B. | 减小、增大 | C. | 增大、增大 | D. | 减小、减小 |
17.对于一定质量的理想气体,下列情况中不可能发生的是( )
| A. | 分子热运动的平均动能不变,分子间的平均距离减小,压强不变 | |
| B. | 分子热运动的平均动能不变,分子间的平均距离减小,压强增大 | |
| C. | 分子热运动的平均动能增大,分子间的平均距离增大,压强增大 | |
| D. | 分子热运动的平均动能减小,分子间的平均距离减小,压强不变 |
7. 图中实线是沿x轴传播的一列简谐横波在t=0时刻的波形图,虚线是这列波在t=0.05s时刻的波形图.已知该波的波速是80cm/s,则下列说法中正确的是 ( )
图中实线是沿x轴传播的一列简谐横波在t=0时刻的波形图,虚线是这列波在t=0.05s时刻的波形图.已知该波的波速是80cm/s,则下列说法中正确的是 ( )
 图中实线是沿x轴传播的一列简谐横波在t=0时刻的波形图,虚线是这列波在t=0.05s时刻的波形图.已知该波的波速是80cm/s,则下列说法中正确的是 ( )
图中实线是沿x轴传播的一列简谐横波在t=0时刻的波形图,虚线是这列波在t=0.05s时刻的波形图.已知该波的波速是80cm/s,则下列说法中正确的是 ( )| A. | 这列波有可能沿x轴正向传播 | |
| B. | 这列波的周期是0.15s | |
| C. | 这列波的波长是10cm | |
| D. | t=0.05s时刻x=6cm处的质点正在向下运动 |

 如图所示电路,M、N是一对间距为d的平行金属板,且将N板接地.已知电源电动势E=36伏,内阻不计,R0=200Ω为定值电阻,R1、R2均为0-999.9Ω的可调电阻箱,用两根绝缘细线将质量为m、带少量负电的小球悬于平行金属板内部.已知细线s水平,线长s=$\frac{d}{3}$.闭合电键k,若分别将R1和R2从200Ω调到400Ω,则两状态小球电势能之比为(小球始终处于静止状态)( )
如图所示电路,M、N是一对间距为d的平行金属板,且将N板接地.已知电源电动势E=36伏,内阻不计,R0=200Ω为定值电阻,R1、R2均为0-999.9Ω的可调电阻箱,用两根绝缘细线将质量为m、带少量负电的小球悬于平行金属板内部.已知细线s水平,线长s=$\frac{d}{3}$.闭合电键k,若分别将R1和R2从200Ω调到400Ω,则两状态小球电势能之比为(小球始终处于静止状态)( )