题目内容
3.组成星球的物质是靠引力吸引在一起的,这样的星球有一个最大的自转角速度,如果超过了该角速度,星球的万有引力将不足以维持其赤道上的物体的圆周运动,则半径为R、密度为ρ、质量均匀分布的星球的最小自转周期T=$\sqrt{\frac{3π}{Gρ}}$(万有引力常量为G).当该星球自转的周期等于最小自转周期的两倍时,该星球表面赤道处物体的重力加速度为πρGR.分析 由题意可知当周期达到某一最小值时,物体对星球表面应刚好没有压力,即万有引力恰好充当星球表面的物体在星球表面做圆周运动的向心力;故由万有引力公式可求得最小周期.
解答 解:根据$F=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}R$可得周期越小,物体需要的向心力越大,物体对星球表面的压力最小,当周期小到一定值时,压力为零,此时万有引力充当向心力,即:
$G\frac{Mm}{{R}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}R$且$M=ρ\frac{4π{R}_{\;}^{3}}{3}$
得$T=\sqrt{\frac{4{π}_{\;}^{2}{R}_{\;}^{3}}{GM}}=\sqrt{\frac{4{π}_{\;}^{2}{R}_{\;}^{3}}{Gρ\frac{4}{3}π{R}_{\;}^{3}}}=\sqrt{\frac{3π}{Gρ}}$
当该星球自转的周期等于最小自转周期的两倍时,
$G\frac{Mm}{{R}_{\;}^{2}}-mg=m\frac{4{π}_{\;}^{2}}{T{′}_{\;}^{2}}R$且T′=2T
所以$mg=\frac{3}{4}G\frac{Mm}{{R}_{\;}^{2}}$
$g=\frac{3}{4}G\frac{M}{{R}_{\;}^{2}}$=$\frac{3}{4}G\frac{ρ\frac{4π{R}_{\;}^{3}}{3}}{{R}_{\;}^{2}}=πρGR$
故答案为:$\sqrt{\frac{3π}{Gρ}}$ πρGR
点评 星球表面的物体受到星球万有引力的作用充当物体的向心力及支持力,星球的转动角速度越大、周期越小时,则需要的向心力越大,则物体所受支持力越小;而当向心力大到一定值时,物体会离开星球表面.

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案| A. | “悟空”的线速度小于同步卫星的速度 | |
| B. | “悟空”的向心加速度小于地球同步卫星的向心加速度 | |
| C. | “悟空”的环绕周期为$\frac{2πt}{β}$ | |
| D. | “悟空”的质量为$\frac{{s}^{3}}{G{t}^{2}β}$T |
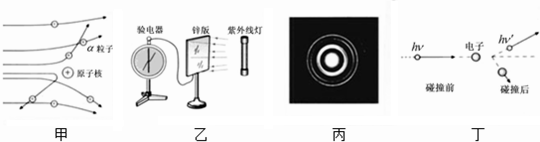
| A. | 甲图和丙图对应的实验,说明了原子内部是非常空旷的,并可以据此估算出原子核的大小 | |
| B. | 通过乙图和丁图对应的实验,用碰撞模型对实验现象做出了解释,使认识到光子具有能量和动量,说明光具有粒子性 | |
| C. | 通过乙图对应的实验,提出光子说,但在认为光有粒子性的同时,并没有否定光的波动性,因为光子的能量E=hν,其中ν为光的频率--这是描述波的物理量之一 | |
| D. | 通过丙图对应的实验,发现电子具有波动性,其波长和动量的关系为λ=hp |
| A. | 4m/s | B. | 5m/s | C. | 10m/s | D. | 50m/s |
| A. | 彗星在近日点的速率大于在远日点的速率 | |
| B. | 彗星在近日点的向心加速度大于在远日点的向心加速度 | |
| C. | 若彗星的周期为75年,则它的半长轴是地球公转半径的75倍 | |
| D. | 彗星在近日点的角速度大于在远日点的角速度 |
| A. | 四颗星围绕正方形对角线的交点做匀速圆周运动 | |
| B. | 四颗星的线速度均为$\sqrt{\frac{Gm}{a}(2+\frac{\sqrt{2}}{4})}$ | |
| C. | 四颗星表面的重力加速度均为$\frac{Gm}{{R}^{2}}$ | |
| D. | 四颗星的周期均为2πa$\sqrt{\frac{2a}{(4+\sqrt{2})Gm}}$ |