题目内容
20.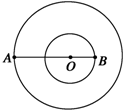 如图所示,双星系统中的星球A、B都可视为质点,A、B绕两者连线上的O点做匀速圆周运动,A、B之间距离不变,观测到A的速率为v、运行周期为T,二者质量分别为m1、m2.则B的周期为T;B的速率为$\frac{{m}_{1}^{\;}v}{{m}_{2}^{\;}}$(用题中物理量字母表示)
如图所示,双星系统中的星球A、B都可视为质点,A、B绕两者连线上的O点做匀速圆周运动,A、B之间距离不变,观测到A的速率为v、运行周期为T,二者质量分别为m1、m2.则B的周期为T;B的速率为$\frac{{m}_{1}^{\;}v}{{m}_{2}^{\;}}$(用题中物理量字母表示)
分析 双星系统构成的条件是双星的角速度相同,依靠它们之间的万有引力提供各自的向心力.由于两星球的加速度不同,必须采用隔离法运用牛顿定律分别对两星球研究,并通过数学变形求解
解答 解:双星是稳定的结构,故公转周期相同,故B的周期也为T.
双星是靠它们之间的万有引力提供向心力有$G\frac{{m}_{1}^{\;}{m}_{2}^{\;}}{{L}_{\;}^{2}}={m}_{1}^{\;}ωv={m}_{2}^{\;}ω{v}_{B}^{\;}$
得${m}_{1}^{\;}v={m}_{2}^{\;}{v}_{B}^{\;}$
解得:${v}_{B}^{\;}=\frac{{m}_{1}^{\;}v}{{m}_{2}^{\;}}$
故答案为:T $\frac{{m}_{1}^{\;}v}{{m}_{2}^{\;}}$
点评 对于天体运动问题关键要建立物理模型.双星问题与人造地球卫星的运动模型不同,两星都绕着它们之间连线上的一点为圆心做匀速圆周运动,双星、圆心始终“三点”一线.

练习册系列答案
相关题目
8.哈雷彗星绕太阳运动的轨道是比较扁的椭圆.下面说法中正确的是( )
| A. | 彗星在近日点的速率大于在远日点的速率 | |
| B. | 彗星在近日点的向心加速度大于在远日点的向心加速度 | |
| C. | 若彗星的周期为75年,则它的半长轴是地球公转半径的75倍 | |
| D. | 彗星在近日点的角速度大于在远日点的角速度 |
15.宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统,通常可忽略其他星体对它们的引力作用.设四星系统中每个星体的质量均为m,半径均为R,四颗星稳定分布在边长为a的正方形的四个顶点上.已知引力常量为G.关于四星系统,下列说法正确的是( )
| A. | 四颗星围绕正方形对角线的交点做匀速圆周运动 | |
| B. | 四颗星的线速度均为$\sqrt{\frac{Gm}{a}(2+\frac{\sqrt{2}}{4})}$ | |
| C. | 四颗星表面的重力加速度均为$\frac{Gm}{{R}^{2}}$ | |
| D. | 四颗星的周期均为2πa$\sqrt{\frac{2a}{(4+\sqrt{2})Gm}}$ |
5.下面是地球、火星的有关情况比较的表格
已知万有引力常量G=6.67×10-11Nm2/kg2,根据以上信息,计算:
①地球与火星(行星的运动可看做圆周运动)万有引力的最大值?(结果保留两位有效数字)
②从某次万有引力最大值至下次万有引力最大之间的时间间隔?(结果保留两位有效数字)
| 星球 | 地球 | 火星 |
| 公转半径 | 1.5×108 km | 2.25×108 km |
| 自转周期 | 23h56min | 24h37min |
| 表面温度 | 15℃ | -100℃~0℃ |
| 公转周期 | 365d | 687d |
| 质量 | 6.0×1024kg | 6.4×1023kg |
①地球与火星(行星的运动可看做圆周运动)万有引力的最大值?(结果保留两位有效数字)
②从某次万有引力最大值至下次万有引力最大之间的时间间隔?(结果保留两位有效数字)
 如图所示,AB为倾角θ=37°的粗糙斜面轨道,通过一小段光滑圆弧与光滑水平轨道BC相连接,质量为m乙的小球乙静止在水平轨道上,质量为m甲的小球甲以速度v0与乙球发生弹性正碰.若m甲:m乙=2:3,且轨道足够长.sin37°=0.6,cos37°=0.8.求:
如图所示,AB为倾角θ=37°的粗糙斜面轨道,通过一小段光滑圆弧与光滑水平轨道BC相连接,质量为m乙的小球乙静止在水平轨道上,质量为m甲的小球甲以速度v0与乙球发生弹性正碰.若m甲:m乙=2:3,且轨道足够长.sin37°=0.6,cos37°=0.8.求: