题目内容
15.在粗糙水平面上静止着一个木块,第一次水平恒力F相作用一段时间t后撤去,木块能继续滑行的距离为s,第二次水平恒力F先作用一段距离s后撤去,木块能继续滑行的时间恰为t.两次运动中木块受到的摩擦力为f,f与F的比值为( )| A. | $\frac{f}{F}$=$\frac{1}{2}$ | B. | $\frac{f}{F}=\frac{1}{3}$ | C. | $\frac{f}{F}=\frac{1}{4}$ | D. | $\frac{f}{F}=\frac{2}{3}$ |
分析 根据牛顿第二定律求出撤去拉力前后的加速度,结合速度时间公式和速度位移公式进行求解.
解答 解:根据牛顿第二定律得,在F作用下的加速度a=$\frac{F-f}{m}$,撤去F后的加速度大小$a′=\frac{f}{m}$,
对于第一次过程,有v=at,$s=\frac{{v}^{2}}{2a′}$,
联立解得$s=\frac{(\frac{F-f}{m})^{2}{t}^{2}}{2\frac{f}{m}}$,①
对于第二次过程,有:$v′=\sqrt{2as}$,t=$\frac{v′}{\frac{f}{m}}$,
联立解得${t}^{2}=\frac{2(F-f)sm}{{f}^{2}}$ ②
解得①②两式解得F=2f,则$\frac{f}{F}=\frac{1}{2}$.
故选:A.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,知道加速度是联系力学和运动学的桥梁,难度中等.

练习册系列答案
相关题目
5. A、B两个点电荷在真空中产生电场的电场线(方向未标出)如图所示.图中C点为两点电荷连线的中点,MN为两点电荷连线的中垂线,D为中垂线上的一点,电场线的分布关于MN左右对称.下列说法中正确的是( )
A、B两个点电荷在真空中产生电场的电场线(方向未标出)如图所示.图中C点为两点电荷连线的中点,MN为两点电荷连线的中垂线,D为中垂线上的一点,电场线的分布关于MN左右对称.下列说法中正确的是( )
 A、B两个点电荷在真空中产生电场的电场线(方向未标出)如图所示.图中C点为两点电荷连线的中点,MN为两点电荷连线的中垂线,D为中垂线上的一点,电场线的分布关于MN左右对称.下列说法中正确的是( )
A、B两个点电荷在真空中产生电场的电场线(方向未标出)如图所示.图中C点为两点电荷连线的中点,MN为两点电荷连线的中垂线,D为中垂线上的一点,电场线的分布关于MN左右对称.下列说法中正确的是( )| A. | 这两个点电荷一定是等量同种电荷 | |
| B. | 这两个点电荷一定是等量异种电荷 | |
| C. | 把某正点电荷q从C点移到D点,电场力做正功 | |
| D. | D点的电场强度可能比C点的电场强度大 |
6.某实验小组利用打点计时器做“研究匀变速直线运动”的实验.

①根据打点计时器打出的纸带,我们可以直接得到的物理量是A
A.时间间隔 B.加速度 C.瞬时速度 D.平均速度
②某同学得到一条用打点计时器打下的纸带如图1所示,并在其上取了A、B、C、D、E、F、G,共7个计数点,每相邻两个计数点间还有4个点图中没有画出,打点计时器接220V、50Hz交流电源.他经过测量并计算得到计时器在打B、C、D、E、F各点时物体的瞬时速度如表:
a.设打点计时器的周期为T,计算vF的公式为vF=$\frac{{d}_{6}-{d}_{4}}{10T}$.
b.根据表中得到的数据,以A点对应的时刻为t=0,试在图2所示的坐标系中合理选择好标度,作出v-t图象(已知打点计时器的周期T=0.02s),并利用该图象求得物体的加速度a=0.40m/s2.

①根据打点计时器打出的纸带,我们可以直接得到的物理量是A
A.时间间隔 B.加速度 C.瞬时速度 D.平均速度
②某同学得到一条用打点计时器打下的纸带如图1所示,并在其上取了A、B、C、D、E、F、G,共7个计数点,每相邻两个计数点间还有4个点图中没有画出,打点计时器接220V、50Hz交流电源.他经过测量并计算得到计时器在打B、C、D、E、F各点时物体的瞬时速度如表:
| 对应点 | B | C | D | E | F |
| 速度(m/s) | 0.141 | 0.180 | 0.218 | 0.262 | 0.301 |
b.根据表中得到的数据,以A点对应的时刻为t=0,试在图2所示的坐标系中合理选择好标度,作出v-t图象(已知打点计时器的周期T=0.02s),并利用该图象求得物体的加速度a=0.40m/s2.
10.2010年6月21日正午时刻,在北半球的A城阳光与竖直方向成7.5°角下射,而在A城正南方,与A城的地面距离为L的B城,阳光恰好沿竖直方向下射,射到地球的太阳光可视为平行光,将地球视为均匀球体,忽略地球自转,用g表示地球表面的重力加速度,G表示引力常量,由此可估算出( )
| A. | 地球半径R=$\frac{48L}{π}$ | |
| B. | 地球的平均密度ρ=$\frac{g}{32GL}$ | |
| C. | 地球第一宇宙速度的表达式v=$\sqrt{\frac{24gL}{π}}$ | |
| D. | 近地卫星的周期T=$\sqrt{\frac{96L}{g}}$ |
20. 在竖直平面内,一根光滑金属杆弯成如图所示形状,相应的曲线方程为y=2.5cos(kx+$\frac{2}{3}π$)(单位:m),式中k=1m-1.将一光滑小环套在该金属杆上,并从x=0处以v0的初速度沿杆向下运动,取重力加速度g=10m/s2.则当小环x轴方向运动的距离大于2π(m),则v0必须满足的条件是( )
在竖直平面内,一根光滑金属杆弯成如图所示形状,相应的曲线方程为y=2.5cos(kx+$\frac{2}{3}π$)(单位:m),式中k=1m-1.将一光滑小环套在该金属杆上,并从x=0处以v0的初速度沿杆向下运动,取重力加速度g=10m/s2.则当小环x轴方向运动的距离大于2π(m),则v0必须满足的条件是( )
 在竖直平面内,一根光滑金属杆弯成如图所示形状,相应的曲线方程为y=2.5cos(kx+$\frac{2}{3}π$)(单位:m),式中k=1m-1.将一光滑小环套在该金属杆上,并从x=0处以v0的初速度沿杆向下运动,取重力加速度g=10m/s2.则当小环x轴方向运动的距离大于2π(m),则v0必须满足的条件是( )
在竖直平面内,一根光滑金属杆弯成如图所示形状,相应的曲线方程为y=2.5cos(kx+$\frac{2}{3}π$)(单位:m),式中k=1m-1.将一光滑小环套在该金属杆上,并从x=0处以v0的初速度沿杆向下运动,取重力加速度g=10m/s2.则当小环x轴方向运动的距离大于2π(m),则v0必须满足的条件是( )| A. | v0≥5$\sqrt{3}$m/s | B. | v0≥0 | C. | v0>5m/s | D. | v0>5$\sqrt{2}$m/s |
7.在同一高度处将三个质量相同的小球,以大小相等的初速度v0分别上抛、平抛和斜抛.下列相关的说法中正确的是( )
| A. | 从抛出到落地过程中,重力对它们做功的平均功率相同 | |
| B. | 从抛出到落地的过程中,重力对它们所做的功相同 | |
| C. | 三个小球落地前瞬间的动能相同 | |
| D. | 三个小球落地前瞬间,重力做功的瞬时功率相同 |
4.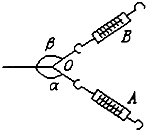 在“探究求合力的方法”的实验中,用两只弹簧测力计A,B把小圆环拉到某一位置O,这时AO,BO间夹角∠AOB<90°,如图所示.现改变弹簧测力计A的拉力方向,使α角减小,但不改变拉力的大小,那么要使小圆环仍被拉到O点,就应调节弹簧测力计B的拉力大小及β角.在下列调整方法中,哪些是可行的 ( )
在“探究求合力的方法”的实验中,用两只弹簧测力计A,B把小圆环拉到某一位置O,这时AO,BO间夹角∠AOB<90°,如图所示.现改变弹簧测力计A的拉力方向,使α角减小,但不改变拉力的大小,那么要使小圆环仍被拉到O点,就应调节弹簧测力计B的拉力大小及β角.在下列调整方法中,哪些是可行的 ( )
 在“探究求合力的方法”的实验中,用两只弹簧测力计A,B把小圆环拉到某一位置O,这时AO,BO间夹角∠AOB<90°,如图所示.现改变弹簧测力计A的拉力方向,使α角减小,但不改变拉力的大小,那么要使小圆环仍被拉到O点,就应调节弹簧测力计B的拉力大小及β角.在下列调整方法中,哪些是可行的 ( )
在“探究求合力的方法”的实验中,用两只弹簧测力计A,B把小圆环拉到某一位置O,这时AO,BO间夹角∠AOB<90°,如图所示.现改变弹簧测力计A的拉力方向,使α角减小,但不改变拉力的大小,那么要使小圆环仍被拉到O点,就应调节弹簧测力计B的拉力大小及β角.在下列调整方法中,哪些是可行的 ( )| A. | 增大B的拉力,同时增大β角 | B. | 增大B的拉力,保持β角不变 | ||
| C. | 保持B的拉力大小不变,增大β角 | D. | 增大B的拉力,同时减小β角 |
5.下列说法正确的是( )
| A. | 楞次通过实验发现了电磁感应现象 | |
| B. | 奥斯特通过实验发现了电流的热效应 | |
| C. | 卡文迪许通过扭秤实验测出了静电力常量 | |
| D. | 法拉第最先提出了“场”的概念,并创造性地用“力线”形像地描述“场”的物理情景 |
