题目内容
13. 相距L=12.5m、质量均为m的两小球A、B,静放在足够长的绝缘水平面上,与水平面间的动摩擦因数均为μ=0.2,其中A电荷量为+q,B不带电.现在水平面附近空间施加一场强大小E=3m/q、水平向右的匀强电场,A开始向右运动,并与B发生多次对心碰撞,且碰撞时间极短,假设每次碰后两球交换速度,A带电量保持不变,B始终不带电,g取10m/s2,求
相距L=12.5m、质量均为m的两小球A、B,静放在足够长的绝缘水平面上,与水平面间的动摩擦因数均为μ=0.2,其中A电荷量为+q,B不带电.现在水平面附近空间施加一场强大小E=3m/q、水平向右的匀强电场,A开始向右运动,并与B发生多次对心碰撞,且碰撞时间极短,假设每次碰后两球交换速度,A带电量保持不变,B始终不带电,g取10m/s2,求(1)第一次碰后B的速度vB1;
(2)从第五次碰撞结束到第六次碰撞开始,B运动的时间tB5;
(3)B运动的总路程x.
分析 (1)第一次碰撞前,推力和滑动摩擦力做功,根据动能定理求解第一次碰撞前A的速度大小,由于发生弹性碰撞,A、B的动量和机械能均守恒,即可求得碰后B的速度大小;
(2)由于质量相等,两个物体交换速度,根据牛顿第二定律和运动学公式分别研究第一次、第二次…第n次碰撞后B的速度大小,即可求得第五次碰撞后至第六次碰撞前B的运动时间;
(3)总结出第n次碰后到第n+1次碰前B的运动位移,运用数学知识求解总路程.
解答 解:(1)A匀加速L,第一次碰前A的速度设为vA1,由动能定理得:
$(F-μmg)L=\frac{1}{2}{mv}_{A1}^{2}$…①
解得:${v}_{A1}=\sqrt{\frac{gL}{5}}$
A与B发生第一次弹性碰撞,遵守动量守恒和机械能守恒,设碰后速度分别为:
v'A1,v'B1mvA1=mv'A1+mv'B1…②
$\frac{1}{2}{mv}_{A1}^{2}=\frac{1}{2}{mv′}_{A1}^{2}+\frac{1}{2}{mv′}_{B1}^{2}$…③
解得:v'A1=0 $v{′}_{B1}=\sqrt{\frac{gL}{5}}$
(2)第一次碰后,设经过t1B停下,B和A位移分别为SB1和SA1
${t}_{1}=\frac{v{′}_{B1}}{μg}$…④
${S}_{B1}=\frac{{v}_{B1}^{2}}{2μg}$…⑤
${S}_{A1}═\frac{1}{2}(\frac{F-μmg}{m}{)t}_{1}^{2}$…⑥
解得:${t}_{1}=\sqrt{\frac{5L}{g}}$${S}_{B1}=\frac{L}{2}$
${S}_{A1}=\frac{L}{4}$
由于SB1>SA1,因此第2次碰前,B已经停下.设第2次碰前A的速度为vA2
$(F-μmg)\frac{L}{2}=\frac{1}{2}{mv}_{A2}^{2}-0$…⑦
A与B发生第2次弹性碰撞,遵守动量守恒和机械能守恒,碰后速度交换,设碰后速度分别为v'A2,v'B2
解得:v'A2=0 $v{′}_{B2}=\sqrt{\frac{gL}{10}}$
同理依此类推,归纳得第n次碰后B的速度为:$v{′}_{Bn}=\sqrt{\frac{gL}{5×{2}^{n-1}}}$
第n次碰后到第n+1次碰前B的运动时间为:${t}_{n}=\frac{v{′}_{Bn}}{μg}$
由此得:${t}_{5}=\sqrt{\frac{5L}{16g}}$
(3)第n次碰后到第n+1次碰前B的运动位移为:${S}_{Bn}=\frac{{v}_{Bn}^{2}}{2μg}$=SB=SB1+SB2+…+SBn=L
答:(1)第一次碰撞后B的速度大小为$\sqrt{\frac{gL}{5}}$;
(2)第五次碰撞后至第六次碰撞前B的运动时间为$\sqrt{\frac{5L}{16g}}$;
(3)B运动的总路程为L.
点评 本题是周期性碰撞类型,运用数学归纳法总结规律是关键.对于第3问也这样求解:最终AB靠在一起停下,由能量守恒得:F(L+SB)=μmg(L+SB)+μmgSB解得SB=L.

 名校课堂系列答案
名校课堂系列答案| A. | 布朗运动就是液体分子的热运动 | |
| B. | 布朗运动图示中不规则折线表示的是液体分子的运动轨迹 | |
| C. | 当分子间的距离变大时,分子间作用力可能减小,也可能增大 | |
| D. | 物体温度改变时物体分子的平均动能可能不改变 |
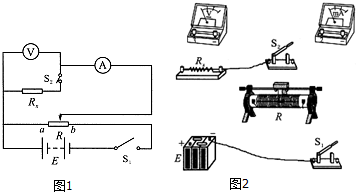
 某同学利用图的实验装置测量重力加速度.测量滑块在运动过程中所受的合外力是“探究动能定理”实验要解决的一个重要问题.
某同学利用图的实验装置测量重力加速度.测量滑块在运动过程中所受的合外力是“探究动能定理”实验要解决的一个重要问题.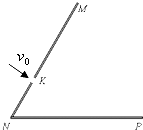 如图所示,倾斜挡板NM上的一个小孔K,NM与水平挡板NP成60°角,K与N间的距离$\overline{KN}$=a.现有质量为m,电荷量为q的正电粒子组成的粒子束,垂直于倾斜挡板NM,以速度v0不断射入,不计粒子所受的重力.
如图所示,倾斜挡板NM上的一个小孔K,NM与水平挡板NP成60°角,K与N间的距离$\overline{KN}$=a.现有质量为m,电荷量为q的正电粒子组成的粒子束,垂直于倾斜挡板NM,以速度v0不断射入,不计粒子所受的重力. 如图所示,在一底边长为2L,底角θ=45°的等腰三角形区域内(O为底边中点)有垂直纸面向外的匀强电场.现有一质量为m,电量为q的带正电粒子从静止开始经过电势差为U的电场加速后,从O点垂直于AB进入磁场,不计重力与空气阻力的影响.
如图所示,在一底边长为2L,底角θ=45°的等腰三角形区域内(O为底边中点)有垂直纸面向外的匀强电场.现有一质量为m,电量为q的带正电粒子从静止开始经过电势差为U的电场加速后,从O点垂直于AB进入磁场,不计重力与空气阻力的影响. 在倾角为30°的光滑固定斜面上,用两根轻绳跨过固定滑轮接在小车上,两端分别悬挂质量为2m和m的物体A、B,当小车静止时两绳分别平行、垂直于斜面,如图所示.不计滑轮摩擦,现使A、B位置互换,当小车再次静止平衡时,
在倾角为30°的光滑固定斜面上,用两根轻绳跨过固定滑轮接在小车上,两端分别悬挂质量为2m和m的物体A、B,当小车静止时两绳分别平行、垂直于斜面,如图所示.不计滑轮摩擦,现使A、B位置互换,当小车再次静止平衡时,