题目内容
9.如图所示,两足够长的平行光滑的金属导轨MN、PQ相距为L=1m,导轨平面与水平面夹角α=30°.磁感应强度为B1=2T的匀强磁场垂直导轨平面向上,长为L=1m的金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m1=2kg、电阻为R1=1Ω.两金属导轨的上端连接右侧电路,电路中通过导线接一对水平放置的平行金属板,两板间的距离和板长均为d=0.5m,定值电阻为R2=3Ω.现闭合开关S并将金属棒由静止释放,重力加速度为g=10m/s2,导轨电阻忽略不计.则:
(1)金属棒下滑的最大速度为多大?
(2)当金属棒下滑达到稳定状态时,水平放置的平行金属板间电场强度是多大?
(3)当金属棒下滑达到稳定状态时,在水平放置的平行金属板间加一垂直于纸面向里的匀强磁场B2=3T,在下板的右端且非常靠近下板的位置有一质量为m2,带电荷量为q=-1×10-4C的微粒以某一初速度水平向左射入两板间,要使该带电微粒在电磁场中恰好做匀速圆周运动并能从金属板间射出,该微粒的初速度应满足什么条件?
分析 (1)ab向下加速运动,切割磁感线产生感应电流,产生阻力,加速度减小,当ab受力平衡时速度达最大,由共点力的平衡条件可得出最大速度;
(2)导体棒中产生电动势,ab与电阻组成闭合回路,由闭合电路的欧姆定律可得金属板间的电压,则可求得内部电场强度;
(3)要使粒子做匀速圆周运动,重力与电场力平衡;由平衡关系可求得粒子的质量;要使粒子飞出,由临界条件可知粒子的半径范围,则可由洛仑兹力充当向心力能求得初速度.
解答 解:(1)当金属棒ab匀速下滑时有m1gsinα=B1IL…①
I=$\frac{E}{{R}_{总}}$ …②
E=B1Lv …③
R总=R1+R2…④
联立①~④式的vm=$\frac{{m}_{1}gsinα({R}_{1}+{R}_{2})}{{B}_{1}^{2}{L}^{2}}$ ⑤
得vm=10m/s
(2)由分压原理得$\frac{{B}_{1}L{v}_{m}}{{R}_{1}+{R}_{2}}$=$\frac{{U}_{c}}{{R}_{2}}$ …⑥
将已知条件代入得UC=15V
故 E=$\frac{{U}_{c}}{d}$=30V/m 方向由上极板指向下极板
(3)要满足题意使带电粒子做匀速圆周运动 则$\frac{q{U}_{c}}{d}$=m2g
由上式可求得 m2=3×10-4㎏…⑦
根据B2qv=$\frac{{m}_{2}{v}^{2}}{r}$
故r=$\frac{{m}_{2}v}{{B}_{2}q}$ …⑧
由题意分析可知,粒子的圆心在磁场的边界上,若能转回到边界处一定从右边飞出,而若半径增大,打在极板上则不会飞出;
但若半径增大到粒子从上板的左侧飞出时,也可飞出,
故要使带电粒子能从金属极板右边射出,必满足r≤$\frac{d}{2}$…⑨
若从左边飞出,则r≥d…⑩
联立⑦⑧⑨式得v≤0.25m/s(从右边射出)
联立⑦⑧⑩式得v≥0.5m/s(从左边射出)
答:(1)最大速度为10m/s;
(2)板间的场强为30V/m;
(3)若从右端射出,速度≤0.25m/s,若从左端射出,速度≥0.5m/s.
点评 本题将电磁感应用带电粒子在混合场中的运动结合在一起,综合性较强,应注意将其分解;
在磁场中时要注意分析临界条件,由几何图形可找出适合条件的物理规律.

 名校课堂系列答案
名校课堂系列答案 如图所示,a,b,c,d是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行.已知a点电势为20V,b点电势为24V.d点电势为12V.一个质子从b点以v0的速度射入电场,入射方向与bc成45°,一段时间后经过C点.不计质子的重力,下列判断正确的是( )
如图所示,a,b,c,d是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行.已知a点电势为20V,b点电势为24V.d点电势为12V.一个质子从b点以v0的速度射入电场,入射方向与bc成45°,一段时间后经过C点.不计质子的重力,下列判断正确的是( )| A. | c点的电势低于a点的电势 | |
| B. | 电场强度方向由b指向d | |
| C. | 质子从b运动到c所用的时间为0 | |
| D. | 质子从b运动到c,电场力做功为4 eV |
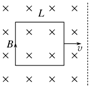 如图所示.边长为L的正方形闭合导线框置于光滑水平面上,有界匀强磁场与水平面垂直.用水平向右的拉力将线框分别以速度v1,v2拉出磁场.下列说法中正确的是( )
如图所示.边长为L的正方形闭合导线框置于光滑水平面上,有界匀强磁场与水平面垂直.用水平向右的拉力将线框分别以速度v1,v2拉出磁场.下列说法中正确的是( )| A. | 若v1>v2,则拉力F1>F2 | |
| B. | 若v1>v2,则通过导线框截面的电荷量q1>q2 | |
| C. | 若v1>v2,则拉力的功率P1=2P2 | |
| D. | 若v1>v2,则线框中产生的热量Q1=2Q2 |
 如图所示,在平面直角坐标系中,有方向平行于坐标平面的匀强电场,其中坐标原点O处的电势为0V,点A处的电势为6V,点B处的电势为3V,则电场强度的大小为( )
如图所示,在平面直角坐标系中,有方向平行于坐标平面的匀强电场,其中坐标原点O处的电势为0V,点A处的电势为6V,点B处的电势为3V,则电场强度的大小为( )| A. | 200 V/m | B. | 200 $\sqrt{3}$ V/m | C. | 100 V/m | D. | 100 $\sqrt{3}$ V/m |

 水平放置的光滑平行金属导轨处于竖直向下的匀强磁场中,导轨的一端接电阻R=1.2Ω,金属棒ab的质量m=0.50kg,电阻r=0.24Ω,在水平恒力F作用下由静止开始向右运动,达到的最大速度v=0.20m/s,电阻R上消耗的最大电功率是P=0.30W.导轨的电阻不计,导轨足够长且与金属棒接触良好.求:
水平放置的光滑平行金属导轨处于竖直向下的匀强磁场中,导轨的一端接电阻R=1.2Ω,金属棒ab的质量m=0.50kg,电阻r=0.24Ω,在水平恒力F作用下由静止开始向右运动,达到的最大速度v=0.20m/s,电阻R上消耗的最大电功率是P=0.30W.导轨的电阻不计,导轨足够长且与金属棒接触良好.求: 如图,水平面(纸面)内间距为l=0.5m的平行金属导轨间接一电阻,质量为m=0.1kg、长度为也为l,电阻为r=0.2Ω的金属杆置于导轨上,t=0时,金属杆在水平向右、大小为F=0.3N的恒定拉力作用下由静止开始运动,t=0.2s时刻,金属杆进入磁感应强度大小为B=0.8T、方向垂直于纸面向里的匀强磁场区域,且在磁场中恰好能保持匀速运动.导轨的电阻均忽略不计,杆与导轨始终保持垂直且接触良好,两者之间的动摩擦因数为μ=0.25.重力加速度大小为g=10m/s2.求:
如图,水平面(纸面)内间距为l=0.5m的平行金属导轨间接一电阻,质量为m=0.1kg、长度为也为l,电阻为r=0.2Ω的金属杆置于导轨上,t=0时,金属杆在水平向右、大小为F=0.3N的恒定拉力作用下由静止开始运动,t=0.2s时刻,金属杆进入磁感应强度大小为B=0.8T、方向垂直于纸面向里的匀强磁场区域,且在磁场中恰好能保持匀速运动.导轨的电阻均忽略不计,杆与导轨始终保持垂直且接触良好,两者之间的动摩擦因数为μ=0.25.重力加速度大小为g=10m/s2.求: 三块相同的金属平板A、B、D自上而下水平放置,间距分别为h和d,如图所示.A、B两板中心开孔,在A板的开孔上搁有一金属容器P,与A板接触良好,其内盛有导电液体.A板通过闭合的电键S与电动势为U0的电池的正极相连,B板与电池的负极相连并接地.容器P内的液体在底部小孔O处形成质量为m,带电量为q的液滴后自由下落,穿过B板的开孔O′落在D板上,其电荷被D板吸附,液体随即蒸发,接着容器底部又形成相同的液滴自由下落,如此继续.设整个装置放在真空中.(g=10m/s2)
三块相同的金属平板A、B、D自上而下水平放置,间距分别为h和d,如图所示.A、B两板中心开孔,在A板的开孔上搁有一金属容器P,与A板接触良好,其内盛有导电液体.A板通过闭合的电键S与电动势为U0的电池的正极相连,B板与电池的负极相连并接地.容器P内的液体在底部小孔O处形成质量为m,带电量为q的液滴后自由下落,穿过B板的开孔O′落在D板上,其电荷被D板吸附,液体随即蒸发,接着容器底部又形成相同的液滴自由下落,如此继续.设整个装置放在真空中.(g=10m/s2)