题目内容
13. 在光滑水平面上,有两个相互接触的物体,如图,已知M>m,第一次用水平力F由左向右推M,物体间的相互作用力为F1;第二次用同样大小的水平力F由右向左推m,物体间的相互作用力为F2,则:( )
在光滑水平面上,有两个相互接触的物体,如图,已知M>m,第一次用水平力F由左向右推M,物体间的相互作用力为F1;第二次用同样大小的水平力F由右向左推m,物体间的相互作用力为F2,则:( )| A. | F1=F2 | B. | F1>F2 | C. | F1<F2 | D. | 无法确定 |
分析 先对整体运用牛顿第二定律求出共同的加速度,对一次对m用牛顿第二定律求出F1,对一次对M用牛顿第二定律求出F2,这样就可以判断F1和F2的大小了.
解答 解:把两个物体看成一个整体,根据牛顿第二定律得:a=$\frac{F}{M+m}$,两次系统的加速度大小相等.
第一次用水平力F由左向右推M,对m运用牛顿第二定理得:F1=ma=$\frac{mF}{M+m}$
第二次用同样大小的水平力F由右向左推m,对M运用牛顿第二定理得:F2=Ma=$\frac{MF}{M+m}$
因为M>m,所以F1<F2
故选:C.
点评 该题是整体法和隔离法的应用,要求同学们能选择恰当的研究对象运用牛顿第二定律解题.

练习册系列答案
相关题目
3. 如图所示,电梯的顶部挂一个弹簧秤,秤下端挂了一个重物,电梯做匀速直线运动时,弹簧秤的示数为10N.某时刻电梯中的人观察到弹簧秤的示数为12N,关于电梯的运动,下列说法正确的是(g取10m/s2)( )
如图所示,电梯的顶部挂一个弹簧秤,秤下端挂了一个重物,电梯做匀速直线运动时,弹簧秤的示数为10N.某时刻电梯中的人观察到弹簧秤的示数为12N,关于电梯的运动,下列说法正确的是(g取10m/s2)( )
 如图所示,电梯的顶部挂一个弹簧秤,秤下端挂了一个重物,电梯做匀速直线运动时,弹簧秤的示数为10N.某时刻电梯中的人观察到弹簧秤的示数为12N,关于电梯的运动,下列说法正确的是(g取10m/s2)( )
如图所示,电梯的顶部挂一个弹簧秤,秤下端挂了一个重物,电梯做匀速直线运动时,弹簧秤的示数为10N.某时刻电梯中的人观察到弹簧秤的示数为12N,关于电梯的运动,下列说法正确的是(g取10m/s2)( )| A. | 电梯可能向上加速运动,加速度大小为2m/s2,物体处于超重状态 | |
| B. | 电梯可能向下加速运动,加速度大小为12m/s2,物体处于失重状态 | |
| C. | 电梯可能向上减速运动,加速度大小为2m/s2,物体处于超重状态 | |
| D. | 电梯可能向下减速运动,加速度大小为12m/s2,物体处于超重状态 |
1. 1922年英国物理学家阿斯顿因质谱仪的发明、同位素和质谱的研究荣获了诺贝尔化学奖.若速度相同的一束粒子由左端射入质谱仪后的运动轨迹如图,则下列正确的是( )
1922年英国物理学家阿斯顿因质谱仪的发明、同位素和质谱的研究荣获了诺贝尔化学奖.若速度相同的一束粒子由左端射入质谱仪后的运动轨迹如图,则下列正确的是( )
 1922年英国物理学家阿斯顿因质谱仪的发明、同位素和质谱的研究荣获了诺贝尔化学奖.若速度相同的一束粒子由左端射入质谱仪后的运动轨迹如图,则下列正确的是( )
1922年英国物理学家阿斯顿因质谱仪的发明、同位素和质谱的研究荣获了诺贝尔化学奖.若速度相同的一束粒子由左端射入质谱仪后的运动轨迹如图,则下列正确的是( )| A. | 该束带电粒子带正电 | |
| B. | 该束带电粒子带负电 | |
| C. | 速度选择器的P1极板带正电 | |
| D. | 在B2磁场中运动半径越大的粒子,比荷$\frac{q}{m}$越小 |
8. 如图所示,倾角为θ的斜面体C置于水平面上,B置于斜面C上,通过细绳跨过光滑的定滑轮与A相连接,连接B的一段细绳与斜面平行,A、B、C都处于静止状态.则( )
如图所示,倾角为θ的斜面体C置于水平面上,B置于斜面C上,通过细绳跨过光滑的定滑轮与A相连接,连接B的一段细绳与斜面平行,A、B、C都处于静止状态.则( )
 如图所示,倾角为θ的斜面体C置于水平面上,B置于斜面C上,通过细绳跨过光滑的定滑轮与A相连接,连接B的一段细绳与斜面平行,A、B、C都处于静止状态.则( )
如图所示,倾角为θ的斜面体C置于水平面上,B置于斜面C上,通过细绳跨过光滑的定滑轮与A相连接,连接B的一段细绳与斜面平行,A、B、C都处于静止状态.则( )| A. | 水平面对C的支持力等于B、C的总重力 | |
| B. | B一定受到C的摩擦力 | |
| C. | C一定受到水平面的摩擦力 | |
| D. | 若将细绳剪断,B物体开始沿斜面向下滑动,则水平面对C的摩擦力可能为零 |
18.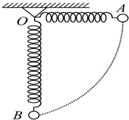 如图所示,一轻弹簧固定于O点,另一端系一重物,将重物从与悬点O在同一水平面且弹簧保持原长的A点无初速度释放,让它自由摆下.不计空气阻力,在重物由A点摆向最低点B的过程中( )
如图所示,一轻弹簧固定于O点,另一端系一重物,将重物从与悬点O在同一水平面且弹簧保持原长的A点无初速度释放,让它自由摆下.不计空气阻力,在重物由A点摆向最低点B的过程中( )
 如图所示,一轻弹簧固定于O点,另一端系一重物,将重物从与悬点O在同一水平面且弹簧保持原长的A点无初速度释放,让它自由摆下.不计空气阻力,在重物由A点摆向最低点B的过程中( )
如图所示,一轻弹簧固定于O点,另一端系一重物,将重物从与悬点O在同一水平面且弹簧保持原长的A点无初速度释放,让它自由摆下.不计空气阻力,在重物由A点摆向最低点B的过程中( )| A. | 重物的重力势能增加 | B. | 弹簧的弹性势能不变 | ||
| C. | 重物的机械能减少 | D. | 重物和弹簧组成的系统机械能减少 |
5. 如图所示,重物B被绕过小滑轮P的细线所悬挂,重物A放在粗糙的水平桌面上;小滑轮P被一根斜短线系于天花板上的Q点;O是三根线的结点,AO水平拉着A物体,C沿竖直方向拉着弹簧,CO与PO夹角为120°;弹簧、细线、滑轮的重力和细线与滑轮间的摩擦力均可忽略,整个装置处于静止状态.其中A重100N,B重40N,A与桌面间的动摩擦因数为0.5,则下列说法正确的是( )
如图所示,重物B被绕过小滑轮P的细线所悬挂,重物A放在粗糙的水平桌面上;小滑轮P被一根斜短线系于天花板上的Q点;O是三根线的结点,AO水平拉着A物体,C沿竖直方向拉着弹簧,CO与PO夹角为120°;弹簧、细线、滑轮的重力和细线与滑轮间的摩擦力均可忽略,整个装置处于静止状态.其中A重100N,B重40N,A与桌面间的动摩擦因数为0.5,则下列说法正确的是( )
 如图所示,重物B被绕过小滑轮P的细线所悬挂,重物A放在粗糙的水平桌面上;小滑轮P被一根斜短线系于天花板上的Q点;O是三根线的结点,AO水平拉着A物体,C沿竖直方向拉着弹簧,CO与PO夹角为120°;弹簧、细线、滑轮的重力和细线与滑轮间的摩擦力均可忽略,整个装置处于静止状态.其中A重100N,B重40N,A与桌面间的动摩擦因数为0.5,则下列说法正确的是( )
如图所示,重物B被绕过小滑轮P的细线所悬挂,重物A放在粗糙的水平桌面上;小滑轮P被一根斜短线系于天花板上的Q点;O是三根线的结点,AO水平拉着A物体,C沿竖直方向拉着弹簧,CO与PO夹角为120°;弹簧、细线、滑轮的重力和细线与滑轮间的摩擦力均可忽略,整个装置处于静止状态.其中A重100N,B重40N,A与桌面间的动摩擦因数为0.5,则下列说法正确的是( )| A. | 弹簧的弹力大小为20N | B. | 桌面对A的摩擦力大小为50N | ||
| C. | 线CO与PO拉力的合力大小为20$\sqrt{3}$N | D. | 线QP与竖直方向的夹角为60° |
3. 如图所示,质量为m的木箱放在水平面上,木箱与水平面间的动摩擦因数为μ,现用斜向下与水平方向成30°角的推力F使木箱匀速运动,以下说法正确的是( )
如图所示,质量为m的木箱放在水平面上,木箱与水平面间的动摩擦因数为μ,现用斜向下与水平方向成30°角的推力F使木箱匀速运动,以下说法正确的是( )
 如图所示,质量为m的木箱放在水平面上,木箱与水平面间的动摩擦因数为μ,现用斜向下与水平方向成30°角的推力F使木箱匀速运动,以下说法正确的是( )
如图所示,质量为m的木箱放在水平面上,木箱与水平面间的动摩擦因数为μ,现用斜向下与水平方向成30°角的推力F使木箱匀速运动,以下说法正确的是( )| A. | 木箱对地面的压力为Fsin30° | |
| B. | 木箱对地面的压力为mg+Fsin30° | |
| C. | 木箱受地面的摩擦力大小为Fcos30° | |
| D. | 木箱受地面的摩擦力大小为μFsin30° |
 如图所示,空间某平面内有一条折线是磁场的分界线,在折线的两侧分布着方向相反、与平面垂直的匀强磁场,磁感应强度大小都为B.折线的顶角∠A=90°,P、Q是折线上的两点,AP=AQ=L.现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出,不计微粒的重力.
如图所示,空间某平面内有一条折线是磁场的分界线,在折线的两侧分布着方向相反、与平面垂直的匀强磁场,磁感应强度大小都为B.折线的顶角∠A=90°,P、Q是折线上的两点,AP=AQ=L.现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出,不计微粒的重力. 某同学利用电压表和电阻箱测定一种特殊电池的电动势,该同学利用如图所示的电路进行实验,图中R0为已知阻值的定值电阻.
某同学利用电压表和电阻箱测定一种特殊电池的电动势,该同学利用如图所示的电路进行实验,图中R0为已知阻值的定值电阻.