题目内容
17. 如图所示,半径为R的半球形陶罐,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合.转台以一定角速度ω匀速转动,一质量为m的小物块落入陶罐内,经过一段时间后,小物块随陶罐一起转动且相对罐壁静止,它和O点的连线与OO′之间的夹角θ为60°.重力加速度大小为g.
如图所示,半径为R的半球形陶罐,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合.转台以一定角速度ω匀速转动,一质量为m的小物块落入陶罐内,经过一段时间后,小物块随陶罐一起转动且相对罐壁静止,它和O点的连线与OO′之间的夹角θ为60°.重力加速度大小为g.(1)若转台处于静止,求物体所受到的支持力和摩擦力;
(2)若ω=ω0,小物块受到的摩擦力恰好为零,求ω0.
分析 (1)若转台处于静止,则物体处于平衡状态,根据力的平衡条件求解;
(2)若ω=ω0,小物块受到的摩擦力恰好为零,靠重力和支持力的合力提供向心力,根据牛顿第二定律求出角速度的大小.
解答 解:(1)若转台处于静止,物体处于平衡状态,受力分析如图所示,根据力的平衡条件
x轴上合力为0:FNsin60°=Ffcos60°
y轴上合力为0:FNcos60°+Ffsin60°=mg
联立解得:FN=$\frac{1}{2}$mg,Ff=$\frac{\sqrt{3}mg}{2}$.
(2)当摩擦力为零,支持力和重力的合力提供向心力,受力分析如图所示,有
由牛顿第二定律得:mgtan60°=m${ω}_{0}^{2}$Rsin60°,
解得:ω0=$\sqrt{\frac{2g}{R}}$.
答:(1)若转台处于静止,物体所受到的支持力为$\frac{1}{2}$mg,摩擦力为$\frac{\sqrt{3}mg}{2}$;
(2)小物块受到的摩擦力恰好为零时的角速度为$\sqrt{\frac{2g}{R}}$.
点评 解决本题的关键搞清物块做圆周运动向心力的来源,结合牛顿第二定律,抓住竖直方向上合力为零,水平方向上的合力提供向心力进行求解.

练习册系列答案
相关题目
20.一人乘坐电梯上楼时,其速度一时间图象如图所示,由图象可知( )


| A. | 该人在0~2s内处于失重状态 | B. | 该人在0~2s内处于超重状态 | ||
| C. | 该人在8~12s内处于失重状态 | D. | 该人在8~12s内处于超重状态 |
2.下列说法正确的是( )
| A. | 光电效应的实验结论是:对于某种金属,用大于其极限频率的入射光照它,则入射光的频率越高,所产生的光电子的最大初动能就越大 | |
| B. | 放射性元素${\;}_{11}^{24}$Na的样品经过6小时后还有$\frac{1}{8}$没有衰变,它的半衰期是4小时 | |
| C. | ${\;}_{90}^{232}$Th衰变成${\;}_{82}^{208}$Pb要经过6次α衰变和4次β衰变 | |
| D. | β衰变中产生的β射线实际上是原子的核外电子挣脱原子核的束缚而形成的 | |
| E. | 氢原子的核外电子由较高能级跃迁到较低能级时,要释放一定频率的光子,同时电子的动能增加,电势能减小 |
9. 两点电荷q1、q2固定在x轴上,在+x轴上每一点的电势φ随x变化的关系如图2所示,其中x=x0处的电势为零,x=x1处的电势最低.下列说法正确的是( )
两点电荷q1、q2固定在x轴上,在+x轴上每一点的电势φ随x变化的关系如图2所示,其中x=x0处的电势为零,x=x1处的电势最低.下列说法正确的是( )
 两点电荷q1、q2固定在x轴上,在+x轴上每一点的电势φ随x变化的关系如图2所示,其中x=x0处的电势为零,x=x1处的电势最低.下列说法正确的是( )
两点电荷q1、q2固定在x轴上,在+x轴上每一点的电势φ随x变化的关系如图2所示,其中x=x0处的电势为零,x=x1处的电势最低.下列说法正确的是( )| A. | x0处的电场强度Ex0=0 | B. | x0、x1处的电场强度Ex0<Ex1 | ||
| C. | q1带正电,q2带负电 | D. | q1的电荷量比q2的大 |
6.美国航空航天局(NASA)于2009年 2月11日晚宣布,美国一颗通信卫星10日与一颗已报废的俄罗斯卫星在太空中相撞,相撞产生的大量碎片对国际空间站等在轨太空设备都造成了潜在威胁.NASA表示,这是人类历史上首次两颗完整在轨卫星相撞事故.新闻发言人凯利•汉弗莱斯表示,撞击地点位于西伯利亚上空约500英里处(约805公里).发生相撞的分别是美国1997年发射的“铱33”卫星,以及俄罗斯1993年发射的“宇宙2251”卫星,据今已经废弃了10年.前者重约560千克,后者重约900千克.假设两颗卫星相撞前都在离地805公里的轨道上做匀速圆周运动,结合中学物理的知识,下面对于二颗卫星说法正确的是( )
| A. | 二者线速度均大于7.9km/s | |
| B. | 二者同方向运行,由于速度大小不同而相撞 | |
| C. | 二者向心力大小相等 | |
| D. | 二者向心加速度大小相等 |
7.火车转弯处的外轨略高于内轨,若火车以规定的车速行驶时,则提供向心力的外力是下列各力中的( )
| A. | 外轨对轮的侧向压力 | B. | 内外轨对轮的侧向压力 | ||
| C. | 火车的重力 | D. | 内外轨对轮的支持力与重力的合力 |
 如图所示,固定在竖着平面内的光滑绝缘管道ABCDQ的A、Q两端与倾角θ=37°的传送带相切.不计管道内外径的差值,AB部分为半径R1=0.4m的圆弧,CDQ部分也是圆弧,D为最高点,BC部分水平,且仅有BC段处于场强大小E=4×I03 N/C、方向水平向右的匀强电场中,传送带长L=1.8m,传送轮半径忽略不计.现将一可视为质点的带正电滑块从传送带上的Q处由静止释放,滑块能从A处平滑进入管道.已知滑块的质量m=lkg、电荷量q=5×10-4C,滑块与传送带之间的动摩擦因数?=0.5,滑块通过管道与传送带的交接处时无速度损失,滑块电荷量始终保持不变,最大静摩擦力等于滑动摩擦力,g=10m/s2.
如图所示,固定在竖着平面内的光滑绝缘管道ABCDQ的A、Q两端与倾角θ=37°的传送带相切.不计管道内外径的差值,AB部分为半径R1=0.4m的圆弧,CDQ部分也是圆弧,D为最高点,BC部分水平,且仅有BC段处于场强大小E=4×I03 N/C、方向水平向右的匀强电场中,传送带长L=1.8m,传送轮半径忽略不计.现将一可视为质点的带正电滑块从传送带上的Q处由静止释放,滑块能从A处平滑进入管道.已知滑块的质量m=lkg、电荷量q=5×10-4C,滑块与传送带之间的动摩擦因数?=0.5,滑块通过管道与传送带的交接处时无速度损失,滑块电荷量始终保持不变,最大静摩擦力等于滑动摩擦力,g=10m/s2.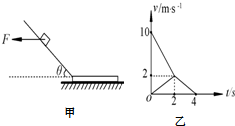 如图甲所示,有一倾角为θ=30°的光滑固定斜面,斜面底端的水平面上放一质量为M的木板,斜面与木板平滑连接,滑块经过斜面与木板交界处的动能损失可忽略不计.开始时,质量为m=1kg的滑块在水平向左的力F作用下静止在斜面上,现将水平力F变为水平向右且大小不变,当滑块滑到木板上时撤去力F,此后滑块和木板在水平面上运动的v-t图象如图乙所示,g取10m/s2.求:
如图甲所示,有一倾角为θ=30°的光滑固定斜面,斜面底端的水平面上放一质量为M的木板,斜面与木板平滑连接,滑块经过斜面与木板交界处的动能损失可忽略不计.开始时,质量为m=1kg的滑块在水平向左的力F作用下静止在斜面上,现将水平力F变为水平向右且大小不变,当滑块滑到木板上时撤去力F,此后滑块和木板在水平面上运动的v-t图象如图乙所示,g取10m/s2.求: