题目内容
12.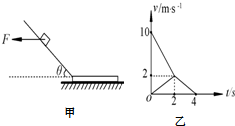 如图甲所示,有一倾角为θ=30°的光滑固定斜面,斜面底端的水平面上放一质量为M的木板,斜面与木板平滑连接,滑块经过斜面与木板交界处的动能损失可忽略不计.开始时,质量为m=1kg的滑块在水平向左的力F作用下静止在斜面上,现将水平力F变为水平向右且大小不变,当滑块滑到木板上时撤去力F,此后滑块和木板在水平面上运动的v-t图象如图乙所示,g取10m/s2.求:
如图甲所示,有一倾角为θ=30°的光滑固定斜面,斜面底端的水平面上放一质量为M的木板,斜面与木板平滑连接,滑块经过斜面与木板交界处的动能损失可忽略不计.开始时,质量为m=1kg的滑块在水平向左的力F作用下静止在斜面上,现将水平力F变为水平向右且大小不变,当滑块滑到木板上时撤去力F,此后滑块和木板在水平面上运动的v-t图象如图乙所示,g取10m/s2.求:(1)水平作用力F的大小;
(2)滑块开始下滑时距木块上表面的高度;
(3)木板的质量M.
分析 (1)对滑块受力分析,由共点力的平衡条件可得出水平作用力的大小;
(2)根据图乙判断滑块滑到斜面底部的速度,由牛顿第二定律求出加速度,从而根据在斜面上的位移和三角关系求出下滑时的高度.
(3)根据图象和牛顿第二定律求出地面和木板间的摩擦力,以及滑块和木板间的摩擦力,进而根据牛顿第二定律求出木板的质量.
解答 解:(1)滑块受到水平推力F、重力mg和支持力N处于平衡,如图所示,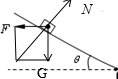
水平推力:F=mgtanθ=1×10×$\frac{\sqrt{3}}{3}$=$\frac{10\sqrt{3}}{3}N$
(2)由图乙知,滑块滑到木板上时速度为:v1=10m/s
设下滑的加速度为a,由牛顿第二定律得:mgsinθ+Fcosθ=ma
代入数据得:a=10m/s2
则下滑时的高度:h=$\frac{{{v}_{1}}^{2}}{2a}•sinθ=\frac{100}{20}•\frac{1}{2}=2.5m$
(3)设在整个过程中,地面对木板的摩擦力为f,滑块与木板间的摩擦力为f1
由图乙知,滑块刚滑上木板时加速度为:${a}_{1}=\frac{△v}{△t}=\frac{2-10}{2-0}=-4m/{s}^{2}$
对滑块:f1=ma1 ①
此时木板的加速度:${a}_{2}=\frac{△v}{△t}=\frac{2-0}{2-0}=1m/{s}^{2}$
对木板:-f1-f=Ma2 ②
当滑块和木板速度相等,均为:v=2m/s之后,连在一起做匀减速直线运动,加速度为:a3=$\frac{△v}{△t}=\frac{0-2}{4-2}=-1m/{s}^{2}$
对整体:-f=(m+M)a3 ③
联立①②③带入数据解得:M=1.5kg
答:(1)水平作用力F的大小为$\frac{10\sqrt{3}}{3}N$;
(2)滑块开始下滑时的高度为2.5m;
(3)木板的质量为1.5kg.
点评 本题考查了牛顿第二定律和运动学公式、共点力平衡的综合运用,关键理清滑块和木板的运动规律,结合牛顿第二定律和运动学公式综合求解.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 在平静的湖面上能看到岸边树的清晰倒影,是发生了光的全反射缘故 | |
| B. | 在光的双缝干涉实验中,把入射光由红光改为蓝光,条纹间距将变宽 | |
| C. | 无色肥皂液吹出的肥皂泡呈彩色是由于光照射时发生了薄膜干涉 | |
| D. | 障碍物的尺寸比光的波长大得多时,不会发生衍射现象 |
 如图所示,在放上小物体A之前,长木板B恰好沿C的足够长斜面匀速下滑,B与斜面间的动摩擦因数为μ,B的上表面光滑,在B匀速下滑过程中轻轻放上小物体A(C物体始终保持静止),下列说法正确的是:( )
如图所示,在放上小物体A之前,长木板B恰好沿C的足够长斜面匀速下滑,B与斜面间的动摩擦因数为μ,B的上表面光滑,在B匀速下滑过程中轻轻放上小物体A(C物体始终保持静止),下列说法正确的是:( )| A. | B仍然匀速下滑 | |
| B. | B减速下滑 | |
| C. | A加速下滑 | |
| D. | 地面对C的摩擦力可能向左、也可能向右 |
| A. | 方程式${\;}_{92}^{238}$U→${\;}_{90}^{234}$Th+${\;}_{2}^{4}$He是重核裂变反应方程 | |
| B. | 光电效应和康普顿效应都说明光具有粒子性 | |
| C. | 衰变所释放的电子是原子核内的中子转化成质子时所产生的 | |
| D. | 比结合能越大,原子核中核子结合的越牢固,原子核越稳定 | |
| E. | 在光电效应实验中,某金属的截止频率对应的波长为λ0,若用波长为λ(λ>λ0)的单色光做该实验,会产生光电效应 |
| A. | 只要能减弱气体分子热运动的剧烈程度,气体的温度就可以降低 | |
| B. | 雪花是晶体,可以有不同的形状 | |
| C. | 当分子间的引力和斥力平衡时,分子势能最大 | |
| D. | 液晶电视的显示器利用了液晶对光具有各向同性作用的特点 | |
| E. | 液体的饱和汽压随温度升高而增大 |


 如图所示,半径为R的半球形陶罐,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合.转台以一定角速度ω匀速转动,一质量为m的小物块落入陶罐内,经过一段时间后,小物块随陶罐一起转动且相对罐壁静止,它和O点的连线与OO′之间的夹角θ为60°.重力加速度大小为g.
如图所示,半径为R的半球形陶罐,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合.转台以一定角速度ω匀速转动,一质量为m的小物块落入陶罐内,经过一段时间后,小物块随陶罐一起转动且相对罐壁静止,它和O点的连线与OO′之间的夹角θ为60°.重力加速度大小为g. 如图,图中坐标原点O(0,0)处有一带电粒子源,沿xOy平面内向y≥0,x≥0的区域内的各个方向发射粒子.粒子的速率均为v,质量均为m,电量均为+q.有人设计了方向垂直于xOy平面向里、磁感应强度为B的匀强磁场区域,使上述所有带电粒子从该区域的边界射出时均能沿y轴负方向运动,不考虑粒子间相互作用,不计粒子重力.试求:
如图,图中坐标原点O(0,0)处有一带电粒子源,沿xOy平面内向y≥0,x≥0的区域内的各个方向发射粒子.粒子的速率均为v,质量均为m,电量均为+q.有人设计了方向垂直于xOy平面向里、磁感应强度为B的匀强磁场区域,使上述所有带电粒子从该区域的边界射出时均能沿y轴负方向运动,不考虑粒子间相互作用,不计粒子重力.试求: