题目内容
10.为了减少因火电站中煤的燃烧对大气的污染而大力发展水电站.三峡水利工程中某水电站发电机组设计为:水以v1=3m/s速度流入水轮机后以v2=1m/s的速度流出.流出水位比流入水位低10m,水流量为Q=10m3/s.水轮机效率为75%,发电效率为80%.发电站通过升压变压器、输电线和降压变压器把电能输送给生产和照明组成的用户.发电机的输出电压是240V,升压变压器原副线圈的匝数之比1:100,输电线上功率损失为5%,用户需要电压为220V,则:(1)发电机组的输出电功率是多少?(g=10m/s2)
(2)输电线的电阻和降压变压器的匝数比为多少?
(3)若有60kW分配给生产用电,其余电能用来照明,那么,可装25W的电灯多少盏?
分析 滑出远距离输电的原理图.根据能量守恒定律得出发电机组的输出功率.结合输电线上损失的功率求出输电线上的电阻.根据输电线上损失的电压求出降压变压器的输入电压,从而得出降压变压器的匝数比.通过能量守恒得出电灯消耗的功率,从而得出电灯的盏数.
解答 解:(1)根据能量守恒得,发电机组的输出功率为:
P=$\frac{mgh+\frac{1}{2}m{(v}_{1}^{2}{-v}_{2}^{2})}{t}×75%×80%$=6.24×105W.
(2)输出电压为:
U2=240×100V=24000V
输送电流为:
I=$\frac{P}{{U}_{2}}=\frac{6.24×1{0}^{5}}{24000}A=26A$
根据${P}_{损}={I}^{2}R=5%P$,得电阻为:R=$\frac{5%P}{{I}^{2}}=\frac{6.24×1{0}^{5}×0.05}{2{6}^{2}}Ω=46Ω$
(3)输电线上的电压损失为:
△U=IR=26×46V=1196V,
则降压变压器的输入电压为:
U3=U2-△U=24000-1196V=22804V
则降压变压器的匝数比为:
$\frac{{n}_{3}}{{n}_{4}}=\frac{{U}_{3}}{{U}_{4}}=\frac{22804}{220}=\frac{5701}{55}$
(4)输电线上损失的功率为:
${P}_{损}=5%P=0.05×6.24×1{0}^{5}$=31200W,
则有:n=$\frac{6.24×1{0}^{5}-31200-60000}{25}$=21312盏.
答:(1)该发电机组的输出功率是6.24×105W;
(2)输电线的电阻为46Ω;
(3)降压变压器的匝数比为5701:55;
(4)若有60kW分配给生产用电,其余电能用来照明,那么,可装25W的电灯的盏数为21312盏.
点评 解决本题的关键知道:1、原副线圈电压、电流和匝数比的关系;2、升压变压器的输出电压、电压损失和降压变压器的输入电压之间的关系.

 口算能手系列答案
口算能手系列答案
| A. | 该交流电流的频率是0.02Hz | |
| B. | 该交流电流的有效值是14.14A | |
| C. | 该交流电流的瞬时值表示式是i=20sin0.02t (A) | |
| D. | 该交流电流的周期是0.01s |
| A. | 狭义相对论认为在不同的惯性参考系中,一切物理规律都是相同的 | |
| B. | 狭义相对论认为在一切惯性系中,光在真空中的速度都等于c,与光源的运动无关 | |
| C. | 狭义相对论只涉及无加速运动的惯性系 | |
| D. | 狭义相对论任何情况下都适用 |
 如图所示是一个由电池、电阻R与平行板电容器组成的串联电路.在只增大电容器两极板间距离的过程中( )
如图所示是一个由电池、电阻R与平行板电容器组成的串联电路.在只增大电容器两极板间距离的过程中( )| A. | 电阻R中没有电流经过 | B. | 电阻R中有电流经过 | ||
| C. | 电阻R中有从a流向b的电流 | D. | 电阻R中有从b流向a的电流 |
 质量为2kg的物体以一定的初速度在水平地面上滑行,在滑行的过程中,其动能随位移的变化关系如图所示,若该物体以12m/s初速度在同一水平地面上滑行,则在水平地面上滑行最大位移为( )
质量为2kg的物体以一定的初速度在水平地面上滑行,在滑行的过程中,其动能随位移的变化关系如图所示,若该物体以12m/s初速度在同一水平地面上滑行,则在水平地面上滑行最大位移为( )| A. | 24m | B. | 18m | C. | 12m | D. | 6m |
 粗糙的水平面上有两个可以视为质点滑块甲、乙,开始时甲、乙均静止,两者相距L=7m,给甲一水平向右的速度v甲=6m/s,给乙一水平向左的速度v乙=2m/s使甲、乙两滑块同时开始在水平面上做匀减速运动,已知两滑块的加速度大小均为α=2m/s2,则下列说法正确的是( )
粗糙的水平面上有两个可以视为质点滑块甲、乙,开始时甲、乙均静止,两者相距L=7m,给甲一水平向右的速度v甲=6m/s,给乙一水平向左的速度v乙=2m/s使甲、乙两滑块同时开始在水平面上做匀减速运动,已知两滑块的加速度大小均为α=2m/s2,则下列说法正确的是( )| A. | 从开始运动计时经(3+$\sqrt{3}$)s的时间两滑块相碰 | |
| B. | 两滑块相碰的地点距离滑块甲的出发点为5.25m | |
| C. | 从开始运动计时经$\frac{4-\sqrt{2}}{2}$s的时间两滑块相碰 | |
| D. | 两滑块相碰的地点距离滑块甲的出发点为6m |
 某同学探究小球沿光滑斜面顶端下滑至底端的运动规律,现将两质量相同的小球同时从斜面的顶端释放,在甲、乙图的两种斜面中,通过一定的判断分析,你可以得到的正确结论是( )
某同学探究小球沿光滑斜面顶端下滑至底端的运动规律,现将两质量相同的小球同时从斜面的顶端释放,在甲、乙图的两种斜面中,通过一定的判断分析,你可以得到的正确结论是( )| A. | 甲图中小球在两个斜面上运动的时间相同 | |
| B. | 甲图中小球在两个斜面上运动的加速度相同 | |
| C. | 乙图中小球在两个斜面上运动的时间相同 | |
| D. | 乙图中小球到达底端时速度大小相同 |
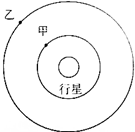 甲、乙两颗卫星绕同一行星做圆周运动,运动方向相同,如图所示,卫星甲的周期为T1,卫星行星乙的周期为T2.若T2>T1,在某一时刻t0两颗卫星相遇(两卫星距离最近),问:
甲、乙两颗卫星绕同一行星做圆周运动,运动方向相同,如图所示,卫星甲的周期为T1,卫星行星乙的周期为T2.若T2>T1,在某一时刻t0两颗卫星相遇(两卫星距离最近),问: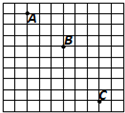 在“研究小球做平抛运动”的实验中:
在“研究小球做平抛运动”的实验中: