题目内容
15.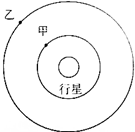 甲、乙两颗卫星绕同一行星做圆周运动,运动方向相同,如图所示,卫星甲的周期为T1,卫星行星乙的周期为T2.若T2>T1,在某一时刻t0两颗卫星相遇(两卫星距离最近),问:
甲、乙两颗卫星绕同一行星做圆周运动,运动方向相同,如图所示,卫星甲的周期为T1,卫星行星乙的周期为T2.若T2>T1,在某一时刻t0两颗卫星相遇(两卫星距离最近),问:(1)至少经过多长时间,两颗卫星又相遇?
(2)至少经过多长时间,两卫星距离最远?
分析 两行星相距最近时,两行星应该在同一半径方向上;两行星相距最远时,两行星应该在同一直径上;由于A的轨道半径小,所以A的角速度大,即A转得较快;当A比B多转一圈时两行星再次相距最近;当A比B多转半圈时两行星相距最远.
解答 解:(1)由题意知,两卫星周期满足T1<T2
某时刻两卫星相距最近,则可知经过时间t1两卫星再次相距最近时,A卫星比B卫星多转过2π弧度,即有:$(\frac{2π}{{T}_{1}}-\frac{2π}{{T}_{2}}){t}_{1}=2π$
所以可得:${t}_{1}=\frac{2π}{\frac{2π}{{T}_{1}}-\frac{2π}{{T}_{2}}}$=$\frac{{T}_{1}{T}_{2}}{{T}_{2}-{T}_{1}}$
(2)同理当两颗卫星经过时间t2两卫星相距最远时,A卫星比B卫星多转过π弧度,即有:
$(\frac{2π}{{T}_{1}}-\frac{2π}{{T}_{2}}){t}_{2}=π$
所以可得:${t}_{2}=\frac{π}{\frac{2π}{{T}_{1}}-\frac{2π}{{T}_{2}}}$=$\frac{{T}_{1}{T}_{2}}{2({T}_{2}-{T}_{1})}$
答:(1)经$\frac{{T}_{1}{T}_{2}}{{T}_{2}-{T}_{1}}$两行星再次相距最近
(2)经$\frac{{T}_{1}{T}_{2}}{2({T}_{2}-{T}_{1})}$两行星相距最远.
点评 根据几何关系得到两颗卫星相距最近和相距最远所满足的角度关系,最近时两卫星在同一半径上角度差为2π弧度,卫星相距最远时,两卫星在同一直径上,转过的角度差为π弧度,这是解决本题的关键.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 如图为某两个电阻的U-I图象,则电阻之比R1:R2,把两电阻串联后接入电路,则消耗功率之比P1:P2,并联后接入电路,消耗功率之比 P1′:P2′,分别为( )
如图为某两个电阻的U-I图象,则电阻之比R1:R2,把两电阻串联后接入电路,则消耗功率之比P1:P2,并联后接入电路,消耗功率之比 P1′:P2′,分别为( )| A. | 2:1 2:1 1:2 | B. | 2:1 1:2 2:1 | ||
| C. | 1:2 1:2 2:1 | D. | 1:2 2:1 1:2 |

| A. | 质点在0和0.8s时刻具有正向最大速度 | |
| B. | 质点在0.2s时刻具有负向最大加速度 | |
| C. | 0至0.4s质点加速度始终指向-x方向不变 | |
| D. | 在0.2s至0.4s时间内,加速度方向和速度方向相同 |
| A. | 发生多普勒效应时,波源的频率发生了变化 | |
| B. | 发生多普勒效应时,观察者接受到的波的频率发生了变化 | |
| C. | 多普勒效应是在波源与观察者之间有相对运动时产生的 | |
| D. | 多普勒效应是由奥地利物理学家多普勒首先发现的 |
 如图所示,一根长杆AB水平放置在地面上,用力拉杆的B端,使它缓慢地转动直立起来,第一次用力F1保持方向竖直向上,第二次用力F2保持方向与杆垂直,两次拉起过程中( )
如图所示,一根长杆AB水平放置在地面上,用力拉杆的B端,使它缓慢地转动直立起来,第一次用力F1保持方向竖直向上,第二次用力F2保持方向与杆垂直,两次拉起过程中( )| A. | F1做功比F2多 | |
| B. | F1做功比F2少 | |
| C. | F1和F2做功一样多 | |
| D. | F1和F2做功不相等,谁多谁少不能确定 |

