题目内容
13.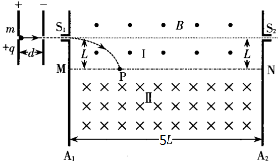 如图所示,足够大的平行挡板A1,A2竖直放置,间距为5L.两板间存在两个方向相反的匀强磁场区域Ⅰ和Ⅱ,磁感应强度大小分别为B和$\frac{2}{3}$B,水平面MN为理想分界线,A1、A2上各有位置正对的小孔S1、S2,两孔与分界面MN的距离均为L.一质量为m、电量为+q的粒子经宽度为d的匀强电场由静止加速后,沿水平方向从S1进入Ⅰ区,粒子重力忽略不计.
如图所示,足够大的平行挡板A1,A2竖直放置,间距为5L.两板间存在两个方向相反的匀强磁场区域Ⅰ和Ⅱ,磁感应强度大小分别为B和$\frac{2}{3}$B,水平面MN为理想分界线,A1、A2上各有位置正对的小孔S1、S2,两孔与分界面MN的距离均为L.一质量为m、电量为+q的粒子经宽度为d的匀强电场由静止加速后,沿水平方向从S1进入Ⅰ区,粒子重力忽略不计.(1)要使粒子不能打到挡板A1上,求匀强电场的电场强度E的最小值.
(2)若粒子能沿水平方向从S2射出,求粒子在磁场中速度大小的所有可能值.
分析 (1)粒子在电场中是直线加速,根据动能定理列式;粒子在磁场中是匀速圆周运动,根据牛顿第二定律列式;结合几何关系得到轨道半径;最后联立求解;
(2)结合几何关系列式求解出轨道半径;粒子在磁场中做匀速圆周运动时,洛伦兹力提供向心力,根据牛顿第二定律列式;最后联立求解即可.
解答 解:(1)粒子在Ⅰ区洛伦兹力提供向心力,故:
qvB=m$\frac{{v}^{2}}{{r}_{1}}$
粒子在Ⅱ区洛伦兹力提供向心力,故:
qv$\frac{2}{3}$B=m$\frac{{v}^{2}}{{r}_{2}}$
所以r2=1.5r1
若要使粒子不能打到挡板A1上,其运动的轨迹如图1,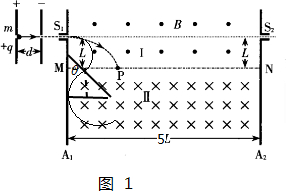
由图中几何关系可得:r1sinθ=r2(1-sinθ)
代入数据整理得:sinθ=0.6
所以θ=37°
在Ⅰ区中:r1+r1cos37°=L
所以${r}_{1}=\frac{1}{1.8}L$
$v=\frac{qBL}{1.8m}$
粒子在电场中,由动能定理,有:
qEmind=$\frac{1}{2}m{v}^{2}-0$
所以:${E}_{min}=\frac{q{B}^{2}{L}^{2}}{6.48md}$
(2)①若粒子能沿水平方向从S2射出,若粒子在Ⅱ区首先粒子不能打到挡板A1上,结合圆周运动的对称性,由几何关系可知:
6r2=$6×1.5{r}_{1}=9×\frac{1}{1.8}L=5L$
由于6r2恰好等于A1,A2之间的间距,所以该种情况下粒子的速度最小,为:${v}_{m}=v=\frac{qBL}{1.8m}$,其运动的轨迹如图2: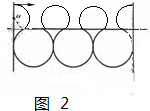
②若粒子在Ⅱ区只发生一次偏转,则运动的轨迹的可能的情况如图3,结合圆周运动的对称性,由几何关系可知: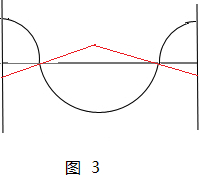
$({r}_{1}-L)^{2}+{L}^{2}={r}_{1}^{2}$
解得:r1=L
此时的速度:$v=\frac{qBL}{m}$
③若粒子在Ⅱ区只发生两次偏转,则运动的轨迹的可能的情况如图4,结合圆周运动的对称性,由几何关系可知: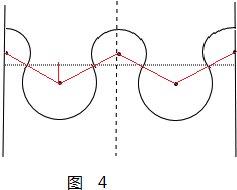
$(L-{r}_{1})^{2}+(\frac{L}{2})^{2}={r}_{1}^{2}$
解得:r1=$\frac{5}{8}$L
此时的速度:$v=\frac{5qBL}{8m}$
答:(1)要使粒子不能打到挡板A1上,匀强电场的电场强度E的最小值是$\frac{q{B}^{2}{L}^{2}}{6.48md}$.
(2)若粒子能沿水平方向从S2射出,粒子在磁场中速度大小的所有可能值是$\frac{qBL}{m}$或$\frac{5qBL}{8m}$或$\frac{qBL}{1.8m}$.
点评 本题关键明确粒子的运动规律,然后分阶段根据动能定理、牛顿第二定律并结合几何关系列式,最后联立求解.在解答的过程中,要注意应用圆周运动的对称性以及Ⅱ区的半径是Ⅰ区半径的1.5倍,所以相应的弦长也是Ⅰ区半径的1.5倍.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案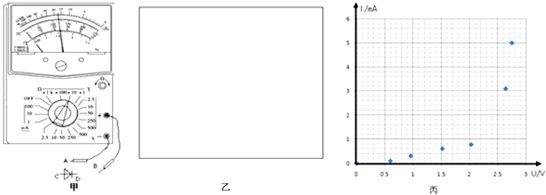
(1)他首先利用多用电表对它的正接时电阻进行粗略测量,如图甲所示,下面说法中正确的是AC
A.欧姆表的表笔A、B应分别接二极管的C、D端
B.双手捏住两表笔金属杆,测量值将偏大
C.若采用“×100”倍率测量时,发现指针偏角过大,应换“×10”倍率,且要重新进行欧姆调零
D.若采用“×10”倍率测量时,发现指针位于刻度“15”与“20”的正中央,测量值应略大于175Ω
(2)为了正确描绘出该二极管正接时的伏安特性曲线,可供选择的器材如下:
A、直流电源E:(电动势为3V,内阻不计) B、开关、导线若干
C、电流传感器mA:(量程-10mA~+10mA,相当于理想电流表,能较为精确测出通过二极管的电流)
D、电压表V:(量程1V,内阻为1kΩ) E、定值电阻R0:阻值为2kΩ
F、滑动变阻器R1:(0~10Ω) G、滑动变阻器R2:(0~1000kΩ)
①实验中滑动变阻器应选R1(选填“R1”或“R2”);
②请在图乙方框中画出实验电路原理图;
③实验记录的8组数据如表所示,其中7组数据的对应点已经标在图丙的坐标纸上,请标出余下一组数据的对应点,并画出I-U图象;
LED蓝光二极管正向伏安特性曲线测试数据表如下:
| I(mA) | 0 | 0.10 | 0.31 | 0.61 | 0.78 | 1.20 | 3.10 | 5.00 |
| U(V) | 0 | 0.61 | 0.96 | 1.52 | 2.03 | 2.35 | 2.64 | 2.75 |

| A. | 图乙所示电压的瞬时值表达式为u=51sin50πt (V) | |
| B. | 变压器原、副线圈中的电流之比为1:4 | |
| C. | 变压器输入、输出功率之比为1:4 | |
| D. | RT处温度升高时,电压表和电流表的示数均变大 |

 空间存在垂直纸面向外的匀强磁场和竖直向上的匀强电场,如图所示,电场强度E=10N/C,PQ为该电磁复合场的分界线,一电量q=2×10-2C,质量m=0.02kg的带正电小物块(可看成质点),以初速度v0=4m/s由M点水平向右射出,恰好由N点(斜面的最高点)沿斜面方向滑入光滑斜面,MN=2$\sqrt{3}$m,已知斜面斜边长为$\frac{8\sqrt{3}}{5}$m,初速度v0方向与MN连线成θ=30°,g=10m/s2,则:
空间存在垂直纸面向外的匀强磁场和竖直向上的匀强电场,如图所示,电场强度E=10N/C,PQ为该电磁复合场的分界线,一电量q=2×10-2C,质量m=0.02kg的带正电小物块(可看成质点),以初速度v0=4m/s由M点水平向右射出,恰好由N点(斜面的最高点)沿斜面方向滑入光滑斜面,MN=2$\sqrt{3}$m,已知斜面斜边长为$\frac{8\sqrt{3}}{5}$m,初速度v0方向与MN连线成θ=30°,g=10m/s2,则: 将硬导线中间一段折成半圆形,使其半径为R,让它在磁感应强度为B、方向如图所示的磁场中绕轴MN匀速转动,转速为n,导线在a、b两处通过电刷与外电路连接,外电路接有额定功率为P的小灯泡并正常发光,电路中除灯泡外,其余部分电阻不计,则灯泡的电阻为$\frac{{(π}^{2}{R}^{2}nB)^{2}}{2P}$.
将硬导线中间一段折成半圆形,使其半径为R,让它在磁感应强度为B、方向如图所示的磁场中绕轴MN匀速转动,转速为n,导线在a、b两处通过电刷与外电路连接,外电路接有额定功率为P的小灯泡并正常发光,电路中除灯泡外,其余部分电阻不计,则灯泡的电阻为$\frac{{(π}^{2}{R}^{2}nB)^{2}}{2P}$.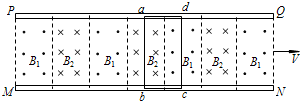 磁悬浮列车是一种高速运载工具,它具有两个重要系统.一是悬浮系统,利用磁力(可由超导电磁铁提供)使车体在导轨上悬浮起来与轨道脱离接触从而减小阻力.另一是驱动系统,即利用磁场与固定在车体下部的感应金属框相互作用,使车体获得牵引力,如图是实验列车驱动系统的原理示意图.在水平面上有两根很长的平行轨道PQ和MN,轨道间有垂直轨道平面的匀强磁场B1和B2,且B1和B2的方向相反,大小相等,即B1=B2=B.在列车的底部固定着绕有N匝相同的闭合矩形金属线圈,并且与之绝缘,整个线圈的总电阻为R,每个矩形金属线圈abcd垂直轨道的边长Lab=L,且两磁场的宽度均与金属线圈ad的边长相同(列车的车厢在图中未画出).当两磁场Bl和B2同时沿导轨方向向右运动时,金属框也会受到向右的磁场力,带动列车沿导轨运动.已知列车车厢及线圈的总质量为M,假设列车所受阻力大小恒为f.则:
磁悬浮列车是一种高速运载工具,它具有两个重要系统.一是悬浮系统,利用磁力(可由超导电磁铁提供)使车体在导轨上悬浮起来与轨道脱离接触从而减小阻力.另一是驱动系统,即利用磁场与固定在车体下部的感应金属框相互作用,使车体获得牵引力,如图是实验列车驱动系统的原理示意图.在水平面上有两根很长的平行轨道PQ和MN,轨道间有垂直轨道平面的匀强磁场B1和B2,且B1和B2的方向相反,大小相等,即B1=B2=B.在列车的底部固定着绕有N匝相同的闭合矩形金属线圈,并且与之绝缘,整个线圈的总电阻为R,每个矩形金属线圈abcd垂直轨道的边长Lab=L,且两磁场的宽度均与金属线圈ad的边长相同(列车的车厢在图中未画出).当两磁场Bl和B2同时沿导轨方向向右运动时,金属框也会受到向右的磁场力,带动列车沿导轨运动.已知列车车厢及线圈的总质量为M,假设列车所受阻力大小恒为f.则: 为了测量一电源的电动势E及内阻r:
为了测量一电源的电动势E及内阻r: